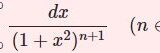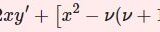整数次の第2種ベッセル関数\begin{equation}Y_n(x)=\displaystyle\lim_{\nu\to n}\frac{\cos\nu\pi J_\nu(x)-J_{-\nu}(x)}{\sin\nu\pi}\tag{1}\end{equation}を級数で書き下す.
ベッセルの微分方程式\begin{equation}x^2y^{\prime\prime}+xy'+(x^2-\nu^2)y=0 \quad (\nu \in \mathbb{R})\tag{2}\end{equation}をフロベニウス法によって解くと,特殊解\begin{equation}J_\nu(x) = \sum^\infty_{m=0}\frac{(-1)^m}{m! \Gamma(m+\nu+1)}\left(\frac{x}{2}\right)^{2m+\nu}\tag{3}\end{equation}を得ます.この $J_\nu(x)$ を第1種ベッセル関数といいます.整数 $n$ に対して $J_n(x)$ と $J_{-n}(x)$ は一次従属であり,\begin{equation}J_n(x)=(-1)^nJ_{-n}(x)\tag{3a}\end{equation}が成立します.
もう1つの特殊解は\begin{equation}\begin{cases}Y_\nu(x)=\displaystyle\frac{\cos\nu\pi J_\nu(x)-J_{-\nu}(x)}{\sin\nu\pi}\quad (\nu\notin\ZZ)\\[1em] Y_n(x)=\displaystyle\lim_{\nu\to n}Y_\nu(x)\quad (n\in\ZZ)\end{cases}\tag{4}\end{equation}この $Y_\nu(x)$ を第2種ベッセル関数といいます.
ベッセルの微分方程式と第1種ベッセル関数の導出については
$\nu\notin\ZZ$ のとき,(4)上段の定義より $Y_\nu(x)$ は特殊解 $J_\nu(x)$ と $J_{-\nu}(x)$ の線型結合ですので,$Y_\nu(x)$ も明らかに(2)の特殊解です.
しかし $\nu\in\ZZ$ では $\dfrac{0}{0}$ の不定形(indeterminate form)です.なぜなら分母は $\sin n\pi=0$ で分子は$$\cos n\pi J_n(x)-J_{-n}(x)=(-1)^nJ_n(x)-J_{-n}(x)=J_{-n}(x)-J_{-n}(x)=0$$と計算されるからです.なのでこの場合は 式(4)下段のように $\nu\to n$ の極限値をとります.実際に極限を計算してみましょう.
まずロピタルの定理によって変形します.\begin{eqnarray*}Y_n(x)&=&\displaystyle\lim_{\nu\to n}\frac{\cos\nu\pi J_\nu(x)-J_{-\nu}(x)}{\sin\nu\pi}\\&=&\displaystyle\lim_{\nu\to n}\frac{\frac{d}{d\nu}\left[\cos\nu\pi J_\nu(x)-J_{-\nu}(x)\right]}{\frac{d}{d\nu}\sin\nu\pi}\\ &=&\displaystyle\lim_{\nu\to n}\frac{-\pi\sin\nu\pi J_\nu(x)+\cos\nu\pi\frac{dJ_\nu}{d\nu}-\frac{dJ_{-\nu}}{d\nu}}{\pi\cos\nu\pi}\\&=&\displaystyle\lim_{\nu\to n}\left[-\tan\nu\pi J_\nu(x)+\frac{1}{\pi}\frac{dJ_\nu}{d\nu}-\frac{1}{\pi\cos\nu\pi}\frac{dJ_{-\nu}}{d\nu}\right]\\ &=&\frac{1}{\pi}\displaystyle\lim_{\nu\to n}\left[\frac{dJ_\nu}{d\nu}-\frac{1}{\cos\nu\pi}\frac{dJ_{-\nu}}{d\nu}\right]\tag{5} \end{eqnarray*}いったんここでストップです.
ここからの計算に当たって予備知識を.ガンマ関数の対数微分をディガンマ関数といい,以下のように定義されます.
\begin{equation}\psi(x)\equiv \left(\ln\G(x)\right)'=\frac{\G'(x)}{\G(x)}\tag{6}\end{equation}
$$\psi(x+1)=\left(\ln\G(x+1)\right)'=\left(\ln\G(x)+\ln x\right)'$$より\begin{equation}\psi(x+1)=\psi(x)+\frac{1}{x}\tag{7}\end{equation}なる漸化式を得ます.またディガンマの特殊値として\begin{equation}\psi(1)=-\g\tag{8}\end{equation}ここで $\g$ はオイラー・マスケローニ定数です.
$\G(x)$ と $\psi(x)$ は ともに $x=0,-1,-2\cdots$ で1位の極をもちます.そこで\begin{eqnarray*}\displaystyle\lim_{x\to 0}\frac{\psi(x)}{\G(x)}&=&\displaystyle\lim_{x\to 0}\frac{x\psi(x)}{x\G(x)}\\&=&\displaystyle\lim_{x\to 0}\frac{x[\psi(x+1)-\frac{1}{x}]}{\G(x+1)}\\&=&\displaystyle\lim_{x\to 0}\frac{x\psi(x+1)-1}{\G(x+1)}\end{eqnarray*}\begin{equation}\therefore\quad\displaystyle\lim_{x\to 0}\frac{\psi(x)}{\G(x)}=-1\tag{9}\end{equation}さらに負整数については $n\in\NN$ として\begin{eqnarray*}\displaystyle\lim_{x\to -n}\frac{\psi(x)}{\G(x)}&=&\displaystyle\lim_{x\to 0}\frac{\psi(x-n)}{\G(x-n)}\\&=&\displaystyle\lim_{x\to 0}\frac{(x-n)\psi(x-n)}{\G(x-n+1)}\\&=&\displaystyle\lim_{x\to 0}\frac{(x-n)[\psi(x-n+1)-\frac{1}{x-n}]}{\G(x-n+1)}\\&=&\displaystyle\lim_{x\to 0}\frac{(x-n)\psi(x-n+1)-1}{\G(x-n+1)}\\&=&\displaystyle\lim_{x\to 0}\left[(x-n)\frac{\psi(x-n+1)}{\G(x-n+1)}-\frac{1}{\G(x-n+1)}\right]\\&=&\displaystyle\lim_{x\to 0}(x-n)\frac{\psi(x-n+1)}{\G(x-n+1)}\\&=&\displaystyle\lim_{x\to -(n-1)}(x-1)\frac{\psi(x)}{\G(x)}\\&=&-n\displaystyle\lim_{x\to -(n-1)}\frac{\psi(x)}{\G(x)}\end{eqnarray*}繰り返して最後に(9)を利用すれば\begin{equation}\therefore\quad\displaystyle\lim_{x\to -n}\frac{\psi(x)}{\G(x)}=n!(-1)^{n-1}\quad(n\in\ZZ^+)\tag{10}\end{equation}
なおガンマ関数についてはこちらで深く学ぶことができます。
というわけで,このあと利用する等式をまとめると
\begin{equation}\psi(x+1)=\psi(x)+\frac{1}{x}\tag{7}\end{equation}\begin{equation}\psi(1)=-\g\tag{8}\end{equation}\begin{equation}\displaystyle\lim_{x\to -n}\frac{\psi(x)}{\G(x)}=n!(-1)^{n-1}\quad(n\in\ZZ^+)\tag{10}\end{equation}
ここで(5)の第1項を計算します.\begin{eqnarray*}\frac{dJ_\nu}{d\nu}&=& \sum_{m=0}^\infty\left[-\frac{(-1)^m\G'(m+\nu+1)}{m!\G^2(m+\nu+1)}\left(\frac{x}{2}\right)^{2m+\nu}+\frac{(-1)^m}{m!\G(m+\nu+1)}\left(\frac{x}{2}\right)^{2m+\nu}\ln\frac{x}{2}\right]\\&=&J_\nu(x)\ln\frac{x}{2}-\sum_{m=0}^\infty\frac{(-1)^m\psi(m+\nu+1)}{m!\G(m+\nu+1)}\left(\frac{x}{2}\right)^{2m+\nu}\quad(\because(6))\end{eqnarray*}
(5)の第2項を計算します.\begin{eqnarray*}\frac{dJ_{-\nu}}{d\nu}&=&\sum_{m=0}^\infty\left[\frac{(-1)^m\G'(m-\nu+1)}{m!\G^2(m-\nu+1)}\left(\frac{x}{2}\right)^{2m-\nu}-\frac{(-1)^m}{m!\G(m-\nu+1)}\left(\frac{x}{2}\right)^{2m-\nu}\ln\frac{x}{2}\right]\\&=&-J_{-\nu}(x)\ln\frac{x}{2}+\sum_{m=0}^\infty\frac{(-1)^m\psi(m-\nu+1)}{m!\G(m-\nu+1)}\left(\frac{x}{2}\right)^{2m-\nu}\quad(\because(6))\end{eqnarray*}
これより(5)は\begin{eqnarray*}\displaystyle\lim_{\nu\to n}\left[\frac{dJ_\nu}{d\nu}-\frac{1}{\cos\nu\pi}\frac{dJ_{-\nu}}{d\nu}\right]&=&J_n(x)\ln\frac{x}{2}-\sum_{m=0}^\infty\frac{(-1)^m\psi(m+n+1)}{m!\G(m+n+1)}\left(\frac{x}{2}\right)^{2m+n}\\&&-(-1)^n\left[-J_{-n}(x)\ln\frac{x}{2}+\sum_{m=0}^\infty\frac{(-1)^m\psi(m-n+1)}{m!\G(m-n+1)}\left(\frac{x}{2}\right)^{2m-n}\right]\\&=&2J_n(x)\ln\frac{x}{2}-\left[\sum_{m=0}^\infty\frac{(-1)^m\psi(m+n+1)}{m!\G(m+n+1)}\left(\frac{x}{2}\right)^{2m+n}+(-1)^n\sum_{m=0}^\infty\frac{(-1)^m\psi(m-n+1)}{m!\G(m-n+1)}\left(\frac{x}{2}\right)^{2m-n}\right]\end{eqnarray*}ただし最後の変形で(3a)を用いました.よって\begin{equation}Y_n(x)=\frac{2}{\pi}J_n(x)\ln\frac{x}{2}-\frac{1}{\pi}\left[\sum_{m=0}^\infty\frac{(-1)^m\psi(m+n+1)}{m!\G(m+n+1)}\left(\frac{x}{2}\right)^{2m+n}+(-1)^n\sum_{m=0}^\infty\frac{(-1)^m\psi(m-n+1)}{m!\G(m-n+1)}\left(\frac{x}{2}\right)^{2m-n}\right]\tag{11}\end{equation}この式より明らかに $Y_n=(-1)^nY_{-n}$ なので $n$ を非負整数に限定して値を求めれば負整数の値もすぐに求まります.
$n=0$ のとき
まず $Y_0$ を求めます.(11)より\begin{eqnarray*}Y_0(x)&=&\frac{2}{\pi}J_0(x)\ln\frac{x}{2}-\frac{1}{\pi}\left[\sum_{m=0}^\infty\frac{(-1)^m\psi(m+1)}{(m!)^2}\left(\frac{x}{2}\right)^{2m}+\sum_{m=0}^\infty\frac{(-1)^m\psi(m+1)}{(m!)^2}\left(\frac{x}{2}\right)^{2m}\right]\\&=&\frac{2}{\pi}J_0(x)\ln\frac{x}{2}-\frac{2}{\pi}\sum_{m=0}^\infty\frac{(-1)^m\psi(m+1)}{(m!)^2}\left(\frac{x}{2}\right)^{2m}\\&=&\frac{2}{\pi}J_0(x)\ln\frac{x}{2}-\frac{2}{\pi}\sum_{m=0}^\infty\frac{(-1)^m}{(m!)^2}(-\g+h_m)\left(\frac{x}{2}\right)^{2m}\quad\because (7)(8)\end{eqnarray*}ここで $h_m$ は調和数で$$h_m\equiv\sum_{k=1}^m\frac{1}{k}\quad,\quad h_0\equiv 0$$よって\begin{equation}Y_0(x)=\frac{2}{\pi}J_0(x)\left(\g+\ln\frac{x}{2}\right)-\frac{2}{\pi}\sum_{m=0}^\infty\frac{(-1)^mh_m}{(m!)^2}\left(\frac{x}{2}\right)^{2m}\tag{12}\end{equation}
$n\ge 1$ のとき
次に自然数次のときの $Y_n$ を求めます.(11)より$$Y_n(x)=\frac{2}{\pi}J_n(x)\ln\frac{x}{2}-\frac{1}{\pi}\left[\sum_{m=0}^\infty\frac{(-1)^m(-\g+h_{m+n})}{m!(m+n)!}\left(\frac{x}{2}\right)^{2m+n}+(-1)^n\sum_{m=0}^\infty\frac{(-1)^m\psi(m-n+1)}{m!\G(m-n+1)}\left(\frac{x}{2}\right)^{2m-n}\right]$$2つ目のシグマの項は\begin{eqnarray*}&&(-1)^n\sum_{m=0}^\infty\frac{(-1)^m\psi(m-n+1)}{m!\G(m-n+1)}\left(\frac{x}{2}\right)^{2m-n}\\&=&(-1)^n\left[\sum_{m=0}^{n-1}\frac{(-1)^m\psi(m-n+1)}{m!\G(m-n+1)}\left(\frac{x}{2}\right)^{2m-n}+\sum_{m=n}^\infty\frac{(-1)^m\psi(m-n+1)}{m!\G(m-n+1)}\left(\frac{x}{2}\right)^{2m-n}\right]\\&=&(-1)^n\left[\sum_{m=0}^{n-1}\frac{(-1)^m\psi(m-n+1)}{m!\G(m-n+1)}\left(\frac{x}{2}\right)^{2m-n}+\sum_{m=0}^\infty\frac{(-1)^{m+n}\psi(m+1)}{(m+n)!m!}\left(\frac{x}{2}\right)^{2m+n}\right]\\&=&(-1)^n\sum_{m=0}^{n-1}\frac{(-1)^m\psi(m-n+1)}{m!\G(m-n+1)}\left(\frac{x}{2}\right)^{2m-n}+\sum_{m=0}^\infty\frac{(-1)^m(-\g+h_m)}{(m+n)!m!}\left(\frac{x}{2}\right)^{2m+n}\\&=&\sum_{m=0}^{n-1}\frac{(n-m-1)!}{m!}\left(\frac{x}{2}\right)^{2m-n}+\sum_{m=0}^\infty\frac{(-1)^m(-\g+h_m)}{(m+n)!m!}\left(\frac{x}{2}\right)^{2m+n}\;\because(10)\end{eqnarray*}よって $Y_n$ は\begin{eqnarray*}Y_n(x)&=&\frac{2}{\pi}J_n(x)\ln\frac{x}{2}\\&&-\frac{1}{\pi}\Biggl[\sum_{m=0}^\infty\frac{(-1)^m(-\g+h_{m+n})}{m!(m+n)!}\left(\frac{x}{2}\right)^{2m+n}\\&&\quad+\sum_{m=0}^{n-1}\frac{(n-m-1)!}{m!}\left(\frac{x}{2}\right)^{2m-n}+\sum_{m=0}^\infty\frac{(-1)^m(-\g+h_m)}{(m+n)!m!}\left(\frac{x}{2}\right)^{2m+n}\Biggr]\\&=&\frac{2}{\pi}J_n(x)\left(\g+\ln\frac{x}{2}\right)\\&&-\frac{1}{\pi}\sum_{m=0}^\infty\frac{(-1)^m(h_m+h_{m+n})}{m!(m+n)!}\left(\frac{x}{2}\right)^{2m+n}-\frac{1}{\pi}\sum_{m=0}^{n-1}\frac{(n-m-1)!}{m!}\left(\frac{x}{2}\right)^{2m-n}\end{eqnarray*}これで整数次の第2種ベッセル関数 $Y_n$ を明示できました!さきほど求めた $Y_0$ と見比べると, 最後のシグマの和をとらないことにすればこの式は $n=0$ でも成立します.
以上により(4)で定義される第2種ベッセル関数 $Y_\nu(x)$ の整数次における明示式は,$n$ を非負整数として
\begin{eqnarray*}Y_n(x)=&&\frac{2}{\pi}J_n(x)\left(\g+\ln\frac{x}{2}\right)\\&&-\frac{1}{\pi}\sum_{m=0}^\infty\frac{(-1)^m(h_m+h_{m+n})}{m!(m+n)!}\left(\frac{x}{2}\right)^{2m+n}\\&&-\frac{1}{\pi}\sum_{m=0}^{n-1}\frac{(n-m-1)!}{m!}\left(\frac{x}{2}\right)^{2m-n}\end{eqnarray*}負整数次は以下により求める.$$Y_{-n}(x)=(-1)^nY_n(x)$$
ベッセル関数の記事
1階非線型微分方程式の例
Anger関数とWeber関数②(ベッセル微分方程式の非斉次解)

Anger関数とWeber関数①(sinやcosの中にsinがある積分)
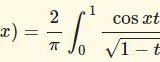
ラプラス変換でベッセル関数の積分表示を作る
第1種変形ベッセル関数の積分表示
【D20】球ベッセルの微分方程式
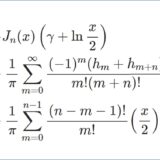
第2種ベッセル関数 $Y_\nu(x)$ の計算
【D19】変形ベッセル微分方程式
【D18】ベッセルの微分方程式と級数解
【物理数学】円筒座標のラプラス方程式とベッセル関数
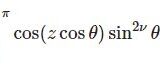
第1種ベッセル関数の積分表示(2) ポアソンの公式の導出
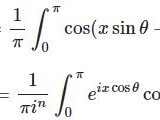
第1種ベッセル関数の積分表示とその導出
【物理数学】N次元グリーン関数の解法(2)
【物理数学】N次元グリーン関数の解法(1)
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。