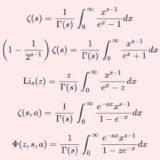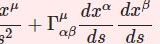位置,速度,加速度,力といったベクトルを極座標成分に分解して表す.基底ベクトルが時間に依存するというデメリットがあるが,ケースによっては圧倒的に便利である.

これまでの話で,物理ではベクトル使えてナンボというのはよくわかったと思うんだ.

平面ではベクトルは必ず2成分だったな.位置,速度,加速度などを $x,y$ 成分で表してきた.

それは任意のベクトルを $x$ 方向の単位ベクトル $\bm{e}_x$ と $y$ 方向の単位ベクトル $\bm{e}_y$ の線型結合で表していることと同じになるんだ.
$$\bm{e}_x\equiv (1,0) \;,\; \bm{e}_y\equiv(0,1)$$たとえば\begin{eqnarray*}(5,2)&=&5\bm{e}_x+2\bm{e}_y\\(x,y)&=& x\bm{e}_x+y\bm{e}_y\\ (v_x,v_y)&=& v_x\bm{e}_x+v_y\bm{e}_y\end{eqnarray*}

当然の話だな.要は直交座標の $xy$ の成分がそのまま係数になっているだけだから簡単だ.

そうなんだ.高校数学でも習ったと思うけど,任意のベクトルは1次独立な2つのベクトルの組の線型結合で表せたよね.その組を「基底ベクトル」というんだ.さっきのは $\bm{e}_x$ と $\bm{e}_y$ を基底ベクトルとして全てのベクトルを表していたのさ.例えば別の基底として $\bm{e}_1=(1,1)$ と $\bm{e}_2=(2,3)$ をとると, $(5,7)$ は
$$(5,7)=\bm{e}_1+2\bm{e}_2$$

ちゃんと表せるんだな.じゃあケースによっては $\bm{e}_x$ と $\bm{e}_y$ とは別の基底をとったほうが分かりやすかったりするのでは?

そういうことさ.今回は極座標バージョンで表す方法を見ていこう!簡単に言うと,物体の位置が $\bm{r}$ のとき,$\bm{r}$ の方向の単位ベクトル $\bm{e}_r$ と,それを90度だけ反時計回りに回転させた $\bm{e}_\t$ を基底にするんだ.
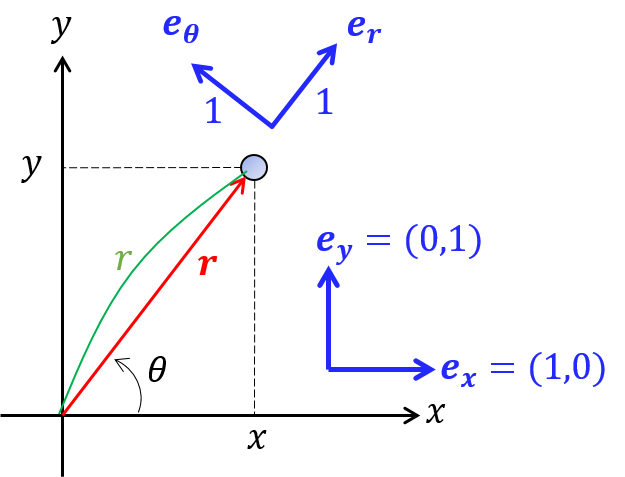
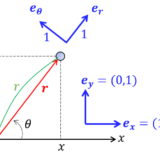
物体の位置 $\bm{r}=(x,y)$ のとき,その方向を動径方向という.動径方向の単位ベクトルを $\bm{e}_r$ と定義する.それを90度反時計回りに回転させたとき,その方向を角度方向といい,単位ベクトルを $\bm{e}_\t$ と定義する.
図より $\bm{r}=r(\cos\t,\sin\t)$ および $\bm{r}=r\bm{e}_r$ だから,$$\bm{e}_r =(\cos\t,\sin\t)$$であることが分かる.$\t$ 方向は$$ \bm{e}_\t =\left(\cos(\t+\frac{\pi}{2}),\sin(\t+\frac{\pi}{2})\right)=(-\sin\t,\cos\t)$$以上から2つの単位ベクトルは\begin{equation}\bm{e}_r =(\cos\t,\sin\t) \tag{1}\end{equation}\begin{equation}\bm{e}_\t =(-\sin\t,\cos\t) \tag{2}\end{equation} と表せる.

ふむ.今回はこの2つのベクトルを基底として,いろいろなベクトルを表していくわけだな.

その通りさ.すでに位置ベクトルは $$\bm{r}=r\bm{e}_r+0\bm{e}_\t$$と表せたね.つまり動径成分が $r$ ,角度成分が $0$ なんだ.あとは速度とか加速度とかも極座標成分で表していこう.

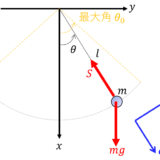
ぼくから練習問題を出すよ!中心力を扱うときは極座標が便利なんだ.
質量 $M$ の太陽が原点にあり,質量 $m$ の惑星が位置 $\bm{r}$ にある.このとき惑星にかかる万有引力の動径成分 $F_r$ ,角度成分 $F_\t$ を求めよ.また万有引力 $\bm{F}$ を $\bm{e}_r$ , $\bm{e}_\t$ を基底として表せ.万有引力定数を $G$ とする.
万有引力の大きさは $$F=\frac{GMm}{r^2}$$であり,向きは中心方向である.よって$$F_r=-\frac{GMm}{r^2}\;,\;F_\t=0$$ベクトルとして表すと$$\bm{F}= F_r \bm{e}_r + F_\t \bm{e}_\t = -\frac{GMm}{r^2} \bm{e}_r $$
問題1の条件もとで $\bm{r}=(x,y)$ とするとき,$\bm{F}$ を $\bm{e}_x$ , $\bm{e}_y$ を基底として表せ.
\begin{eqnarray*}\bm{F}&=&-\frac{GMm}{r^2}\bm{e}_r=-\frac{GMm}{r^3}\bm{r}\\&=& -\frac{GMm}{r^3}(x,y)\\&=& -\frac{GMm}{(x^2+y^2)^\frac{3}{2}}(x\bm{e}_x+y\bm{e}_y)\\&=& -\frac{GMmx}{(x^2+y^2)^\frac{3}{2}}\bm{e}_x-\frac{GMmy}{(x^2+y^2)^\frac{3}{2}}\bm{e}_y\end{eqnarray*}

万有引力のベクトルを問題1,2で2通り表したけど,極座標のほうが見やすいね!

気づいたんだけど,物体が動いたら $\bm{r}$ の方向って刻々と変わるんじゃない?てことは今回の基底ベクトルは時間の関数になるよな.

いいところに気づいたね.その通りなんだ.明示すると $\bm{e}_r(t)$ みたいになるね.今後の学習のために基底ベクトルの時間微分を試しておこう!ちなみに時間微分はドット( $\dot{X}$ ) で表すよ.
式(1)(2)を再掲する.物体の位置 $\bm{r}$ に対し,\begin{equation}\bm{e}_r =(\cos\t,\sin\t) \tag{1}\end{equation}\begin{equation}\bm{e}_\t =(-\sin\t,\cos\t) \tag{2}\end{equation}一般に物体は移動するから $r,\t$ は時間の関数である.そのため $\bm{e}_r$ , $\bm{e}_\t$ も時間の関数である.微分すると\begin{eqnarray*}\dot{\bm{e}_r}&=&\frac{d}{dt}\binom{\cos\t}{\sin\t}=\dot{\t}\binom{-\sin\t}{\cos\t}\\&=&\dot{\t}\bm{e}_\t\end{eqnarray*}\begin{eqnarray*}\dot{\bm{e}_\t}&=&\frac{d}{dt}\binom{-\sin\t}{\cos\t}=\dot{\t}\binom{-\cos\t}{-\sin\t}\\&=&-\dot{\t}\bm{e}_r\end{eqnarray*}となる.まとめると\begin{equation}\dot{\bm{e}_r}=\dot{\t}\bm{e}_\t\tag{3}\end{equation} \begin{equation}\dot{\bm{e}_\t}=-\dot{\t}\bm{e}_r\tag{4}\end{equation}

割とスッキリと表せるんだな.これを使って速度や加速度を求めていこう.

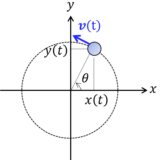
速度は位置の時間微分,加速度はさらにその時間微分だね.これらの極座標成分を求めよう!式(3)(4)を使うよ.
位置ベクトルは$$\bm{r}=r\bm{e}_r$$これの時間微分が速度だから\begin{eqnarray*}\bm{v}&=&\dot{r}\bm{e}_r+r\dot{\bm{e}_r}\\&=&\dot{r}\bm{e}_r+r\dot{\t}\bm{e}_\t\quad(\because(3))\end{eqnarray*}よって速度の動径成分・角度成分による表式$$\bm{v}=v_r\bm{e}_r+v_\t\bm{e}_\t$$と比べて\begin{equation}\begin{cases}v_r&=&\dot{r}\\v_\t &=& r\dot{\t}\end{cases}\tag{5}\end{equation}
加速度は速度の微分だから\begin{eqnarray*}\bm{a}&=& \frac{d}{dt}\left(\dot{r}\bm{e}_r+r\dot{\t}\bm{e}_\t\right)\\&=&\ddot{r}\bm{e}_r+\dot{r}\dot{\bm{e}_r}+\dot{r}\dot{\t}\bm{e}_\t+ r\ddot{\t}\bm{e}_\t+ r\dot{\t}\dot{\bm{e}_\t}\\&=& \ddot{r}\bm{e}_r+\dot{r}\dot{\t}\bm{e}_\t+\dot{r}\dot{\t}\bm{e}_\t+ r\ddot{\t}\bm{e}_\t-r\dot{\t}^2\bm{e}_r\quad(\because(3)(4))\\&=& (\ddot{r}- r\dot{\t}^2)\bm{e}_r+(2\dot{r}\dot{\t}+r\ddot{\t})\bm{e}_\t \end{eqnarray*}よって加速度の動径成分・角度成分による表式$$\bm{a}=a_r\bm{e}_r+a_\t\bm{e}_\t$$と比べて\begin{equation}\begin{cases}a_r&=& \ddot{r}- r\dot{\t}^2 \\a_\t &=& 2\dot{r}\dot{\t}+r\ddot{\t} \end{cases}\tag{6}\end{equation}

微分で機械的に導出したけど,速度の式(5)を見てイメージはつかめそう?

動径方向はまあ当然の式だよな.角度方向は中心からの距離と角速度の積になっている.円運動の式 $v=r\omega$ のように,中心からの距離が大きいほど,角度の変化が大きいほど $\theta$ 方向の速度は大きい.
加速度の式(6)はちょっと分かりにくいな.

じゃあ円運動に限定してみようか.$r$ を定数にすれば $\dot{r}=0$ で $\ddot{r}=0$ だから
$$\begin{cases}a_r&=& - r\dot{\t}^2 \\a_\t &=& r\ddot{\t} \end{cases}$$

角速度 $\dot{\t}=\omega$ と書くとより見やすいかもしれない.
$$\begin{cases}a_r&=& -r\omega^2\\a_\t &=& r\dot{\omega} \end{cases}$$

あー,$a_r$ はまさに向心加速度だ.$a_\t$ がゼロでなかったら角速度が変化するってことだから,これは角度成分のスピードを変化させるものだな.まさに角度方向の加速度というにふさわしい.

そうなんだ.そういうイメージをもったうえで,今後は極座標を実践でも扱えるようにしていこう!

ぼくだよ!ここまでの内容を練習問題で実践してみよう!
$\bm{v}=\dot{r}\bm{e}_r+r\dot{\t}\bm{e}_\t$ を2乗し,速さ $v$ を求めよ.
内積であることに注意する.定義より明らかに $\bm{e}_r\cdot\bm{e}_\t=0$ および $\bm{e}_r^2= \bm{e}_\t^2=1$であるから\begin{eqnarray*}v^2&=& (\dot{r}\bm{e}_r+r\dot{\t}\bm{e}_\t)\cdot (\dot{r}\bm{e}_r+r\dot{\t}\bm{e}_\t) \\&=&\dot{r}^2+r^2\dot{\t}^2\end{eqnarray*}$$\therefore\quad v=\sqrt{ \dot{r}^2+r^2\dot{\t}^2}$$

簡単のために,同一ベクトルどうしの内積は $\bm{A}^2$ のように書いたよ.速さは速度ベクトルの大きさだから $v=|\bm{v}|$ なんだ!
角速度 $\omega$ の等速円運動における $\bm{v}$ と $\bm{a}$ の極座標成分を求めよ.
半径 $r$ と 角速度 $\dot{\t}=\omega$ が一定だから$$\dot{r}=\ddot{r}=\ddot{\t}=0$$よって(5)(6)より極座標成分は $$\begin{cases}v_r&=&0\\v_\t &=& r\omega\end{cases}$$$$\begin{cases}a_r&=& - r\omega^2 \\a_\t &=& 0\end{cases}$$

各成分の値を,高校の等速円運動の知識とリンクさせておこうね!
$xy$ 平面上の位置 $\bm{r}$ にある質量 $m$ の質点が,原点へ向かう方向に大きさ $kr$ の力を受けるとする(フックの法則もどき).ただし $r=|\bm{r}|$. このとき動径成分と角度成分の運動方程式を記せ.
また,このとき $r^2\dot{\t}$ は時間によらず一定であることを示せ.
かかる力は$$\bm{F}=-kr\bm{e}_r$$加速度は$$\bm{a}=(\ddot{r}- r\dot{\t}^2)\bm{e}_r+(2\dot{r}\dot{\t}+r\ddot{\t})\bm{e}_\t$$である.運動方程式 $\bm{F}=m\bm{a}$ より$$ -kr\bm{e}_r = m(\ddot{r}- r\dot{\t}^2)\bm{e}_r+(2\dot{r}\dot{\t}+r\ddot{\t})\bm{e}_\t $$動径・角度成分の運動方程式は$$\therefore\begin{cases}-kr=m(\ddot{r}- r\dot{\t}^2)\\0= 2\dot{r}\dot{\t}+r\ddot{\t} \end{cases} $$
また,$r^2\dot{\t}$ を時間微分すると$$\frac{d}{dt}(r^2\dot{\t})=2r\dot{r}\dot{\t}+r^2\ddot{\t}=r( 2\dot{r}\dot{\t}+r\ddot{\t} )=0$$よって時間によらず一定である.

最後の変な問題は,角運動量保存とかかわっているよ!中心力の場合に現れる式なんだ.いずれ紹介するね.

3次元バージョンの記事もあるけど,ちょっと根気がいるよ!よかったら読んでみてね。
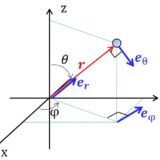 空間ベクトルの球座標成分
空間ベクトルの球座標成分
微積分と高校物理シリーズ
【H7】単振り子の方程式と厳密解
【H6】ベクトルの極座標成分
【H5】等速・非等速円運動と微分方程式

【H4】ばねの微分方程式 水平・鉛直・空気抵抗
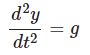
【H3】落体運動の法則はただ1つ
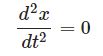
【H2】力がゼロの運動方程式と等速直線運動
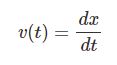
【H1】力学の表現と本シリーズの意義
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。