単振り子は,振れ幅が小さいときは単振動と見なせ,周期は振れ幅に依存しないと高等学校で学習する.ここでは振れ幅が小さくないときにも適用できるように方程式を厳密に考えよう.

今日は単振り子をやるよ!

高校では振幅が小さいと仮定して,水平な単振動と見なしていたな.

振幅の大小に関わらず,広く適用できるように考えてみよう.まず座標を決めるよ.振り子の特徴は,糸の長さが一定だから,質点ともう片方の端っことの距離が変わらないことさ.だから糸を固定している点を原点として極座標にすると分かりやすいよ.
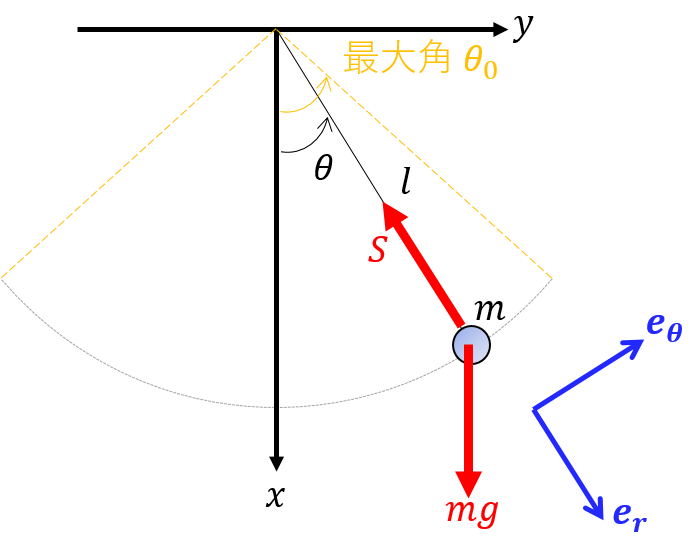

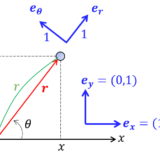
前回勉強したようにベクトルを極座標成分で表現するといいんだな.図からして,加速度ベクトルの極座標は次のように求まる.
質点 $m$ の位置は $\bm{r}= l\bm{e}_r$.両辺を微分すると$$\bm{v}=l\dot{\t}\bm{e_\t}$$再度微分すると$$\bm{a}=-l\dot{\t}^2\bm{e}_r+l\ddot{\t}\bm{e}_\t$$

かかっている力は大きさ $S$ の張力と $mg$ の重力さ.$mg$ は動径方向と角度方向に分解しよう.
$$\bm{F}=(mg\cos\t-S)\bm{e}_r-mg\sin\t\bm{e}_\t$$よって $\bm{F}=m\bm{a}$ から$$(mg\cos\t-S)\bm{e}_r-mg\sin\t\bm{e}_\t=-ml\dot{\t}^2\bm{e}_r+ml\ddot{\t}\bm{e}_\t$$両辺を比べると, $\theta$ 成分に関して成り立つ等式は
\begin{equation}\ddot{\theta} =-\frac{g}{l}\sin\theta\tag{1}\end{equation}

かなりシンプルだ.ちなみに動径方向の運動方程式は放置なの?

張力 $S(t)$ について知りたいなら議論してもいいんだけど,今はいらないかな.
そして,(1)はシンプルな微分方程式に見えるけど,実は解けない.

じゃあここで終了なのか。。。

まぁある意味終了といえるんだけど,何も進展しないわけじゃあないんだ.後で詳細に解説するよ.それよりまず,高校の知識を確認しておこうか.振れ幅が小さければ,(1)で $\theta$ が小さいということだから,$\sin\theta\approx\theta$ だね.あと水平方向の座標は $y\approx l\theta$ だね.
$$\ddot{\theta} \approx-\frac{g}{l}\theta\Longrightarrow \theta\approx \theta_0\sin\sqrt{\frac{g}{l}}t$$$$\therefore\quad y\approx l\theta_0\sin\sqrt{\frac{g}{l}}t$$これは水平方向の単振動であることを示す.この式より周期は $$T=2\pi\sqrt{\frac{l}{g}}$$であり,振幅 $l\t_0$ によらず一定.

うんうん。簡単な微分方程式だな.$\theta\approx\sin\t$ の近似も高校物理で頻出だった.

そうそう.今日はこの近似ナシでさらに進めていくよ!

この近似は $\sin x$ のマクローリン展開から理解できるよ!
$$\sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\cdots+\frac{(-1)^n}{(2n+1)!}x^{2n+1}+\cdots$$

$x$ が小さければ $x\ll 1$ だから,$x^3$ はもっと小さいし,$x^5$ はもっともっと小さいんだ.だから高次の項はぜーんぶ無視できるんだ.
$$x\ll1\Longrightarrow \sin x\approx x$$

さて,角度成分の運動方程式に話を戻そう.
\begin{equation}\ddot{\theta} =-\frac{g}{l}\sin\theta\tag{1}\end{equation}

定数はひとまとめにしようか.
$\omega\equiv\sqrt{\frac{g}{l}}$ とおくと$$\ddot{\theta} =-\omega^2\sin\theta$$

よくある手段なんだけど,両辺に $\dot{\t}$ をかけてみるよ.
$$\dot{\t}\ddot{\theta} =-\omega^2\dot{\t}\sin\theta$$$$\therefore\quad \frac{1}{2}\frac{d}{dt}(\dot{\t}^2)=\omega^2\frac{d}{dt}(\cos\t)$$

両辺を $t$ で積分するんだ.時刻 $t=0$ において $\theta$ は最大値 $\theta_0$ をとって,そのときの角速度 $\dot{\theta}(0)=0$ とするよ.
$$\int_0^t\left[\frac{d}{dt}(\dot{\t}^2)\right]dt=2\omega^2\int_0^t\left[\frac{d}{dt}(\cos\t)\right]dt$$$$\dot{\t}^2=2\omega^2(\cos\theta-\cos\theta_0)$$半角の公式から$$\dot{\t}^2=4\omega^2\left( \sin^2\frac{\theta_0}{2}-\sin^2\frac{\theta}{2}\right)$$
ここで $\dot{\theta}=\displaystyle\frac{d\theta}{dt}$ なので$$\therefore dt=\frac{d\theta}{2\omega\sqrt{\sin^2\frac{\theta_0}{2}-\sin^2\frac{\theta}{2}}}$$ただし $\dot{\t}\ge 0$ の区間だけ考えたため,根号の前の複号は必要ない.おもりの運動の対称性から周期の1/4すなわち $\theta :0\rightarrow\theta_0$ の範囲で積分すると$$\frac{T}{4}=\frac{1}{2\omega}\int_0^{\theta_0}\frac{d\theta}{\sqrt{\sin^2\frac{\theta_0}{2}-\sin^2\frac{\theta}{2}}}$$よって周期の式は
\begin{equation}T=\frac{2}{\omega}\int_0^{\theta_0}\frac{d\theta}{\sqrt{\sin^2\frac{\theta_0}{2}-\sin^2\frac{\theta}{2}}}\tag{2}\end{equation}

なんだかんだで周期を計算する式ができあがったけど,ここからは進まないな.

うん.この積分は求まらないんだ.「解析的に解けない」というよ.$\sin$ とか $\log$ とか多項式とか,そういった初等的な関数で表せないんだ.でも(2)で終わってしまうと周期がどんな量になるかまったく分からないし,ちょっとごり押ししてみるね.

とりあえず,積分を少し見やすくするね.
$$\sin\displaystyle\frac{\theta}{2}=\sin\frac{\theta_0}{2}\sin\phi$$と変数変換する.さらに $\displaystyle\sin\frac{\theta_0}{2}=k$ とすれば$$T=\frac{4}{\omega}\int^\frac{\pi}{2}_0\frac{d\phi}{\sqrt{1-k^2\sin^2\phi}}$$と書き直せる.

これは第1種完全楕円積分とよばれるよ!見やすくなったけどやっぱり積分できないんだ.

こういう場合の打開策は?

必殺「無限級数」があるよ.まず下のような関数 $f(x)$ を考えよう.$f(x)$ はマクローリン展開によって無限級数でも表せるんだ.
$$f(x)=\frac{1}{\sqrt{1-x}}$$$$\frac{1}{\sqrt{1-x}}=\sum^\infty_{n=0}\frac{(2n-1)!!}{(2n)!!}x^n$$

詳細は端折るけど,マクローリン展開は下のような展開をいうぞ.よかったら上の $f(x)$ で試してみてね.
$$f(x)=\sum^\infty_{n=0}\frac{f^{(n)}(0)}{n!}x^n$$

この展開式に $x=k^2\sin^2\phi$ を代入しよう.
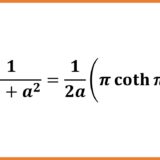
\begin{eqnarray*}T&=&\frac{4}{\omega}\sum^\infty_{n=0}\frac{(2n-1)!!}{(2n)!!}k^{2n}\int^\frac{\pi}{2}_0\sin^{2n}\phi d\phi\\&=&\frac{4}{\omega}\sum^\infty_{n=0}\frac{(2n-1)!!}{(2n)!!}k^{2n}\cdot \frac{(2n-1)!!}{(2n)!!}\cdot\frac{\pi}{2}\\&=&\frac{2\pi}{\omega}\sum^\infty_{n=0}\left(\frac{(2n-1)!!}{(2n)!!}k^n\right)^2\\&=&\frac{2\pi}{\omega}\sum^\infty_{n=0}\left(\frac{(2n-1)!!}{(2n)!!}\sin^n\frac{\theta_0}{2}\right)^2\end{eqnarray*}以上より $\omega=\sqrt{\displaystyle\frac{g}{l}}$ と戻して
$$T=2\pi\sqrt{\frac{l}{g}}\sum^\infty_{n=0}\left( \frac{(2n-1)!!}{(2n)!!}\sin^{n}\frac{\theta_0}{2}\right)^2$$

これで周期が分かったね.まぁ無限級数だから分かりにくい形だけど.この式から分かる通り,周期 $T$ は厳密には最大角度 $\t_0$ に依存するんだ.いわゆる「等時性」は成り立たないよ.

でも最大角度 $\t_0$ が小さいときは高校物理の周期の式と等しくなるはずだ.$\t_0\ll1$ なら $\sin\frac{\t_0}{2}\ll 1$ だから,下のように高次項は無視できる.
\begin{eqnarray*}T&=&2\pi\sqrt{\frac{l}{g}}\sum^\infty_{n=0}\left( \frac{(2n-1)!!}{(2n)!!}\sin^{n}\frac{\theta_0}{2}\right)^2\\&=&2\pi\sqrt{\frac{l}{g}}\left[1+\left(\frac{1}{2}\sin\frac{\theta_0}{2}\right)^2+\left(\frac{3}{8}\sin^2\frac{\theta_0}{2}\right)^2+\cdots\right]\\&\approx&2\pi\sqrt{\frac{l}{g}}\end{eqnarray*}

ちゃんと等しくなった!

そのとおりなんだ!今回の話は数学的に少し難解だったぶん,いろんな学びがあったんじゃないかな.

ぼくから練習問題だよ!今回の記事に関する応用問題は特にないから,ここで使った数学テクニックの練習をしよう.
ばねにつながれた質点の運動方程式$$ma=-kx$$の両辺に $v$ をかけることにより,力学的エネルギー保存則を導け.
$\dot{v}=a$ , $\dot{x}=v$ であることを用いる.$$mav=-kxv$$は以下のように書き直せる.$$\frac{d}{dt}\left(\frac{1}{2}mv^2\right)=\frac{d}{dt}\left(-\frac{1}{2}kx^2\right)$$$$\therefore\quad\frac{d}{dt}\left(\frac{1}{2}mv^2+\frac{1}{2}kx^2\right)=0$$この式は $\frac{1}{2}mv^2+\frac{1}{2}kx^2$ が時間によって変化しない,すなわち保存することを示す.よって力学的エネルギー保存則を表現している.
同様の方法により,微分方程式$$\ddot{\t}=\t^3$$から1階の微分方程式を導出せよ.
両辺に $\dot{\t}$ をかけると$$\frac{d}{dt}(\dot{\t}^2)=\frac{1}{2}\frac{d}{dt}(\t^4)$$を得る.よって積分すると$$\dot{\t}^2=\frac{1}{2}\t^4+C$$これは1階の微分方程式である.
正弦関数が以下のように級数で表せるとする.$$\sin x=a_0+a_1x+a_2x^2+a_3x^3+\cdots$$両辺を繰り返し微分することにより,$a_0$ , $a_1$ , $a_2$ , $a_3$ を求めよ.
$x=0$ を代入すると $a_0=0$.
微分して$$\cos x=a_1+2a_2x+3a_3x^2+\cdots$$$x=0$ を代入すると $a_1=1$.
再度微分して$$-\sin x=2a_2+6a_3x+\cdots$$$x=0$ を代入すると $a_2=0$.
以下同様に $a_3=-1/6$.
これがマクローリン展開の手順であり,$$\sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\cdots+\frac{(-1)^n}{(2n+1)!}x^{2n+1}+\cdots$$とあらわせる.
自然数 $n$ に対し$$\int^\frac{\pi}{2}_0\sin^{2n}x dx$$を求めよ.
$I_n=\displaystyle\int^\frac{\pi}{2}_0\sin^{2n}x dx$ とおくと\begin{eqnarray*}I_n&=&\left[-\cos x\sin^{2n-1}x\right]+(2n-1)\int_0^\frac{\pi}{2}\cos^2x\sin^{2n-2}xdx\\&=&(2n-1)I_{n-1}-(2n-1)I_n\end{eqnarray*}$$\therefore\quad I_n=\frac{2n-1}{2n}I_{n-1}=\frac{(2n-1)(2n-3)}{2n(2n-2)}I_{n-2}=\cdots =\frac{(2n-1)!!}{(2n)!!}I_0$$$$\therefore\quad I_n=\frac{(2n-1)!!}{(2n)!!}\frac{\pi}{2}$$

今回の記事でも分かるように,物理の勉強を進めるにはどうしても数学を応用できる必要があるんだ.頑張っていろいろ計算できるようになろうね!
微積分と物理シリーズ
【H7】単振り子の方程式と厳密解
【H6】ベクトルの極座標成分
【H5】等速・非等速円運動と微分方程式

【H4】ばねの微分方程式 水平・鉛直・空気抵抗
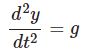
【H3】落体運動の法則はただ1つ
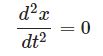
【H2】力がゼロの運動方程式と等速直線運動
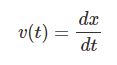
【H1】力学の表現と本シリーズの意義
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。