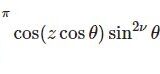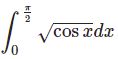関数を１回微分すると１階微分、２回なら2階微分といいます。では整数でない、例えば半分回の微分というものは考えられるでしょうか。一般化の過程を見ていきましょう。
関数$f(x)$を１回微分すると１階微分、２回なら2階微分といいます。このように関数をどんどん微分していくと、$$f'(x),f^{\prime\prime}(x),f^{\prime\prime\prime}(x),\cdots , f^{(n)}(x)$$となります。
では整数でない、例えば半分回の微分というものは考えられるでしょうか。
$$D=\frac{d}{dx}$$と書くことにします。整数階微分のときは$$D^2f=D(Df)$$
であり、$$D^{m+n}=D^mD^n$$ですから、「半分回」のときもそのルールが守られるべきです。つまり、$$D^{1/2}D^{1/2}=D$$半階微分を２度行うと１階導関数となることが要請されるのです。
具体的に考えていきます。整数階微分の方法は高校数学で学習していますので、その方法を非整数へ拡張してみます。
まず整数階微分の既知のこととして、$f(x)=x^n$の$k$階導関数は$$f^{(k)}(x)=D^kx^n=n(n-1)\cdots(n-k+1)x^{n-k}=\frac{n!}{(n-k)!}x^{n-k}$$となります。階乗をガンマ関数であらわせば、$$D^k(x^n)=\frac{\Gamma(n+1)}{\Gamma(n-k+1)}x^{n-k}$$ここで、試しに $k=1/2$ としてみると、$$D^\frac{1}{2}x^n=\frac{\Gamma(n+1)}{\Gamma(n+\frac{1}{2})}x^{n-1/2}=\frac{(2n)!!}{(2n-1)!!\sqrt{\pi}}x^{n-\frac{1}{2}}$$なお、$\Gamma(1/2)=\sqrt\pi$ を用いています。
半階微分をこのように定式化すると、
- 整数階微分の拡張であることが直感的に分かる
- $x$の次数がちゃんと$1/2$下がっている
と言えます。ぱっと見て係数が複雑ですが、
3. 半階微分を２度行うと１階導関数となる
ことを確認して正当化しましょう。半階微分を２回実行すると、$$D^\frac{1}{2}D^\frac{1}{2}x^n=D^\frac{1}{2}\left[\frac{\Gamma(n+1)}{\Gamma(n+\frac{1}{2})}x^{n-\frac{1}{2}}\right]=\frac{\Gamma(n+1)}{\Gamma(n+\frac{1}{2})}\cdot\frac{\Gamma(n+\frac{1}{2})}{\Gamma(n)}x^{n-1}=nx^{n-1}$$となり、確かに1階導関数となりました。
同様に1/3階微分や、1/4階微分といったものも定式化できます。こういった数学の分野を分数階微積分学といいます。
Please support me!
記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。
