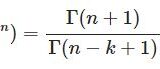N次元グリーン関数を求める際に用いた、ベッセル関数のとある積分表示（ポアソンの公式）について論じます。この表示の特徴はコサインの中にコサインがある積分がベッセル関数とガンマ関数によって表せるというところです。ベッセル関数の級数表示からスタートして、少々面倒ではあるものの比較的平易な計算で導出可能です。
\begin{equation}\int^\pi_0\cos(z\cos\theta)\sin^{2\nu}\theta d\theta=\frac{\sqrt{\pi}\Gamma(\nu+\frac{1}{2})}{(z/2)^\nu}J_\nu(z)\quad(\nu>-\frac{1}{2})\tag{1}\end{equation}
第1種ベッセル関数 $J_\nu(x)$ には多様な表示がありますが、今回もその１つです。過去に $N$ 次元グリーン関数の記事を書いたときに「Lommelの積分表示」という名前でこの公式を紹介したものの、これを導出してはいなかったので一度やってみようと思いました。しかも調べていくとこの公式の名前は"Poisson's Bessel Function Formula"らしく、『岩波数学公式III』に載っている「Lommelの積分表示」という名前は一般的でないのかもしれません。
【物理数学】N次元グリーン関数の解法(2)
また過去にベッセル関数の積分表示第1弾を書いているので参考にしてください。今回の記事とはまた違った数学テクニックが学べます。
第1種ベッセル関数の積分表示とその導出
ラプラス変換でベッセル関数の積分表示を作る
では話をはじめていきます。そもそも第1種ベッセル関数は「ベッセルの微分方程式」というものの解であり、以下のように級数表示されます。
\begin{equation}J_\nu(z)=\sum^\infty_{m=0}\frac{(-1)^m}{m!\Gamma(m+\nu+1)}\left(\frac{z}{2}\right)^{2m+\nu}\tag{2}\end{equation}
なんでそうなるという話は別記事で書いていますので，ここではとりあえず認めてください。この関数がどうして(1)を満たすのか考えていきます。
まず唐突なのですが$$\int^1_{-1}e^{izx}(1-x^2)^{\nu-\frac{1}{2}}dx$$なる積分を考えます。$e^X$のマクローリン展開を用いて\begin{eqnarray*} \int^1_{-1}e^{izx}(1-x^2)^{\nu-\frac{1}{2}}dx &=& \int^1_{-1}\sum_{n=0}^\infty\frac{(izx)^n}{n!}(1-x^2)^{\nu-\frac{1}{2}}dx \\&=&\sum_{n=0}^\infty\frac{(iz)^n}{n!} \int^1_{-1}x^n(1-x^2)^{\nu-\frac{1}{2}}dx\end{eqnarray*}最右辺の被積分関数は $n$ が奇数のとき奇関数であり、偶数のとき偶関数ですので $n=2m$ のみ考えればよく \begin{eqnarray*} \int^1_{-1}e^{izx}(1-x^2)^{\nu-\frac{1}{2}}dx &=& \sum_{m=0}^\infty\frac{(iz)^{2m}}{(2m)!}\cdot 2\int^1_0 x^{2m}(1-x^2)^{\nu-\frac{1}{2}}dx\\&=& \sum_{m=0}^\infty\frac{(-1)^m z^{2m}}{(2m)!}\cdot 2\int^1_0 x^{2m}(1-x^2)^{\nu-\frac{1}{2}}dx\\&=& \sum_{m=0}^\infty\frac{(-1)^m z^{2m}}{(2m)!}\int^1_0 y^{m}(1-y)^{\nu-\frac{1}{2}}\frac{dy}{\sqrt{y}}\\&=& \sum_{m=0}^\infty\frac{(-1)^m z^{2m}}{(2m)!}\int^1_0 y^{m-\frac{1}{2}}(1-y)^{\nu-\frac{1}{2}}dy\\&=& \sum_{m=0}^\infty\frac{(-1)^m z^{2m}}{(2m)!}B\left(m+\frac{1}{2},\nu+\frac{1}{2}\right)\\&=& \sum_{m=0}^\infty\frac{(-1)^m z^{2m}}{(2m)!}\frac{\Gamma(m+\frac{1}{2})\Gamma(\nu+\frac{1}{2})}{\Gamma(m+\nu+1)}\end{eqnarray*}ここでは置換 $x^2=y$ およびベータ関数の定義$$B(x,y)=\int_0^1t^{x-1}(1-t)^{y-1}dt$$およびベータ関数とガンマ関数の関係式$$B(x,y)=\frac{\Gamma(x)\Gamma(y)}{\Gamma(x+y)}$$を使いました。最後に現れるガンマ関数のうち\begin{eqnarray*}\Gamma\left(m+\frac{1}{2}\right)&=&(m-\frac{1}{2})(m-\frac{3}{2})\cdots\frac{3}{2}\frac{1}{2}\Gamma\left(\frac{1}{2}\right)\\&=& (m-\frac{1}{2})(m-\frac{3}{2})\cdots\frac{3}{2}\frac{1}{2}\sqrt{\pi}\\&=& \frac{(2m-1)!!}{2^m}\sqrt{\pi}\end{eqnarray*}と変形を施せば \begin{eqnarray*} \int^1_{-1}e^{izx}(1-x^2)^{\nu-\frac{1}{2}}dx &=& \sqrt{\pi}\sum_{m=0}^\infty\frac{(-1)^m z^{2m}}{(2m)!}\frac{(2m-1)!!}{2^m}\frac{\Gamma(\nu+\frac{1}{2})}{\Gamma(m+\nu+1)}\\&=& \sqrt{\pi}\Gamma(\nu+\frac{1}{2})\sum_{m=0}^\infty\frac{(-1)^m z^{2m}}{(2m)!!}\frac{1}{2^m}\frac{1}{\Gamma(m+\nu+1)}\\&=& \sqrt{\pi}\Gamma(\nu+\frac{1}{2})\sum_{m=0}^\infty\frac{(-1)^m z^{2m}}{m!2^{2m}}\frac{1}{\Gamma(m+\nu+1)}\\&=& \sqrt{\pi}\Gamma(\nu+\frac{1}{2})\sum_{m=0}^\infty\frac{(-1)^m}{m!\Gamma(m+\nu+1)}\left(\frac{z}{2}\right)^{2m}\\&=& \frac{\sqrt{\pi}\Gamma(\nu+\frac{1}{2})}{(z/2)^\nu} \sum_{m=0}^\infty\frac{(-1)^m}{m!\Gamma(m+\nu+1)}\left(\frac{z}{2}\right)^{2m+\nu}\\&=& \frac{\sqrt{\pi}\Gamma(\nu+\frac{1}{2})}{(z/2)^\nu} J_\nu(z) \quad\because(2) \end{eqnarray*}\begin{equation} \int^1_{-1}e^{izx}(1-x^2)^{\nu-\frac{1}{2}}dx = \frac{\sqrt{\pi}\Gamma(\nu+\frac{1}{2})}{(z/2)^\nu} J_\nu(z)\tag{3}\end{equation}というわけで第1種ベッセル関数が現れ、(1)の右辺が見えてきました。
(3)の左辺を変形していきます。$x=\cos\theta$ とし\begin{eqnarray*} \int^1_{-1}e^{izx}(1-x^2)^{\nu-\frac{1}{2}}dx&=& \int^0_{\pi}e^{iz\cos\theta}\sin^{2\nu-1}\theta(-\sin\theta) d\theta\\&=& \int^\pi_0e^{iz\cos\theta}\sin^{2\nu}\theta d\theta\\&=& \int^\pi_0 \cos(z\cos\theta)\sin^{2\nu}\theta d\theta+i\int^\pi_0 \sin(z\cos\theta)\sin^{2\nu}\theta d\theta\end{eqnarray*}最後の虚部の積分は区間を半分に分けて後半のほうを $\phi=\pi-\theta$ と置換します。\begin{eqnarray*} \int^\pi_0 \sin(z\cos\theta)\sin^{2\nu}\theta d\theta &=& \int^\frac{\pi}{2}_0 \sin(z\cos\theta)\sin^{2\nu}\theta d\theta+ \int^\pi_\frac{\pi}{2} \sin(z\cos\theta)\sin^{2\nu}\theta d\theta\\&=& \int^\frac{\pi}{2}_0 \sin(z\cos\theta)\sin^{2\nu}\theta d\theta+ \int^0_\frac{\pi}{2} \sin(-z\cos\phi)\sin^{2\nu}\phi (-d\phi)\\&=& \int^\frac{\pi}{2}_0 \sin(z\cos\theta)\sin^{2\nu}\theta d\theta+ \int^0_\frac{\pi}{2} \sin(z\cos\phi)\sin^{2\nu}\phi d\phi\\&=& 0\end{eqnarray*}$$\therefore\quad \int^1_{-1}e^{izx}(1-x^2)^{\nu-\frac{1}{2}}dx = \int^\pi_0 \cos(z\cos\theta)\sin^{2\nu}\theta d\theta $$
(3)より以下の結論を得ます。
\begin{equation}\int^\pi_0\cos(z\cos\theta)\sin^{2\nu}\theta d\theta=\frac{\sqrt{\pi}\Gamma(\nu+\frac{1}{2})}{(z/2)^\nu}J_\nu(z)\end{equation}
変形ベッセル関数でも同様のことをやりました
第1種変形ベッセル関数の積分表示
Please support me!
記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。
