微分幾何学の講座・第9回。曲線におけるフレネ・セレの公式の、曲面バージョンであるガウスの公式とワインガルテンの公式を導出します。接続係数が登場。

計算が面倒だけど、やっていることは平易だよ。過去記事から順に見るといいよ。
前回はこちら:
もくじ
こちらで学んだように、第1基本量は\begin{equation}E:=\bm{S}_u\cdot \bm{S}_u \;,\quad F:=\bm{S}_u\cdot \bm{S}_v\;,\quad G:=\bm{S}_v\cdot \bm{S}_v\tag{1}\end{equation}第2基本量は\begin{equation}L:=\bm{S}_{uu}\cdot \bm{n}\;,\quad M:=\bm{S}_{uv}\cdot \bm{n}\;,\quad N:=\bm{S}_{vv}\cdot \bm{n}\tag{2}\end{equation}と定義されます。文字の見た目は定数ぽい感じですが、歴とした $u,v$ の関数です。なお第2基本量については\begin{equation}L=-\bm{S}_{u}\cdot \bm{n}_{u}\;,\quad M=-\bm{S}_{u}\cdot \bm{n}_{v}\;,\quad N=-\bm{S}_{v}\cdot \bm{n}_{v}\tag{2'}\end{equation}とも書けるのでした。
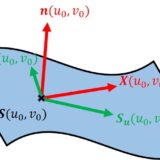
過去記事では、曲面 $\bm{S}(u,v)$ において、偏微分によって得られる2つの接ベクトル $\bm{S}_u(u,v)$ , $\bm{S}_v(u,v)$ および単位法ベクトル $\bm{n}(u,v)$ は1次独立であることを説明しました(単位法ベクトルは $\bm{S}_u(u,v)\times\bm{S}_v(u,v)$ の向きで長さ1)。

よって空間内の任意のベクトルはこれら3つの線型結合で表すことができます。ただし、このとき基底 $\bm{S}_u$ , $\bm{S}_v$ , $\bm{n}$ はパラメータ $u,v$ によって変化します。曲線論において動標構 $\bm{e}_1$ , $\bm{e}_2$ , $\bm{e}_3$ を基底として議論したのと同様です。そこでは動標構の変化 $\bm{e}'_1$ , $\bm{e}'_2$ , $\bm{e}'_3$ を動標構で表しました(フレネ・セレの公式)。
今回は $\bm{S}_u$ , $\bm{S}_v$ , $\bm{n}$ の変化を $\bm{S}_u$ , $\bm{S}_v$ , $\bm{n}$ で表現してみましょう。
接ベクトルおよび単位法ベクトル $\bm{S}_u$ , $\bm{S}_v$ , $\bm{n}$ の変化とはすなわち$$\bm{S}_{uu},\bm{S}_{uv} ,\bm{S}_{vv} , \bm{n}_u,\bm{n}_v$$です。これらの量を $\bm{S}_u$ , $\bm{S}_v$ , $\bm{n}$ の線型結合で表すと\begin{eqnarray*}\bm{S}_{uu} &=& a_{11}\bm{S}_u+b_{11}\bm{S}_v+c_{11}\bm{n}\\ \bm{S}_{uv} &=& a_{12}\bm{S}_u+b_{12}\bm{S}_v+c_{12}\bm{n}\\\bm{S}_{vv} &=& a_{22}\bm{S}_u+b_{22}\bm{S}_v+c_{22}\bm{n}\\[1em]\bm{n}_u &=& a_1\bm{S}_u+b_1\bm{S}_v+c_1\bm{n}\\\bm{n}_v &=& a_2\bm{S}_u+b_2\bm{S}_v+c_2\bm{n}\end{eqnarray*}それぞれの式の両辺と $\bm{n}$ との内積をとります。左辺については(2)および $\bm{n}\cdot\bm{n}=1$ の偏微分を考えて $\bm{n}_u\cdot\bm{n}=\bm{n}_v\cdot\bm{n}=0$ となっていることを用います。右辺については $\bm{S}_u$ , $\bm{S}_v$ が $\bm{n}$ に直交することを利用します。すると$$c_{11}=L\;,\;c_{12}=M\;,\;c_{22}=N\;,\;c_1=c_2=0$$と分かりますので\begin{equation}\begin{cases}\bm{S}_{uu} &=& a_{11}\bm{S}_u+b_{11}\bm{S}_v+L\bm{n}\\[1em] \bm{S}_{uv} &=& a_{12}\bm{S}_u+b_{12}\bm{S}_v+M\bm{n}\\[1em]\bm{S}_{vv} &=& a_{22}\bm{S}_u+b_{22}\bm{S}_v+N\bm{n}\end{cases}\tag{3}\end{equation}
\begin{equation}\begin{cases}\bm{n}_u &=& a_1\bm{S}_u+b_1\bm{S}_v\\[1em]\bm{n}_v &=& a_2\bm{S}_u+b_2\bm{S}_v\end{cases}\tag{4}\end{equation}となります。
(3)の係数を求めていきましょう。準備として(1)を微分することにより\begin{equation}\begin{cases}E_u=2\bm{S}_u\cdot\bm{S}_{uu}\;,&\; E_v=2\bm{S}_u\cdot\bm{S}_{uv}\\[0.5em] F_u=\bm{S}_v\cdot\bm{S}_{uu}+\bm{S}_u\cdot\bm{S}_{uv}\;,&\; F_v=\bm{S}_u\cdot\bm{S}_{vv}+\bm{S}_v\cdot\bm{S}_{uv}\\[0.5em] G_u=2\bm{S}_v\cdot\bm{S}_{uv}\;,&\; G_v=2\bm{S}_v\cdot\bm{S}_{vv}\end{cases}\tag{5}\end{equation}(3)の両辺と $\bm{S}_u$ との内積をとった式、および $\bm{S}_v$ との内積をとった式において、左辺では(5)を、右辺では(1)(2)を用いることにより、次の連立方程式を得ます。\begin{equation}\begin{pmatrix}E & 0 & 0 & F & 0 & 0 \\ 0 & E & 0 & 0 & F & 0 \\ F & E & 0 & G & F & 0 \\ 0 & F & E & 0 & G & F \\0 & F & 0 & 0 & G & 0 \\ 0 & 0 & F & 0 & 0 & G\end{pmatrix}\begin{pmatrix}a_{11}\\a_{12}\\a_{22}\\b_{11}\\b_{12}\\b_{22}\end{pmatrix} =\begin{pmatrix}\frac{1}{2}E_u \\\frac{1}{2}E_v \\ F_u \\ F_v \\ \frac{1}{2}G_u \\ \frac{1}{2}G_v\end{pmatrix}\tag{6}\end{equation}これを解くと\begin{equation}\begin{pmatrix}a_{11}\\a_{12}\\a_{22}\\b_{11}\\b_{12}\\b_{22}\end{pmatrix}=\frac{1}{2(EG-F^2)}\begin{pmatrix}E_uG+F(E_v-2F_u)\\E_vG-FG_u\\-FG_v-G(G_u-2F_v)\\-E_uF-E(E_v-2F_u)\\-E_vF+EG_u\\EG_v+F(G_u-2F_v)\end{pmatrix}\tag{7}\end{equation}よって次の定理を得ます。
接ベクトルの偏微分は次のように表される。\begin{equation}\begin{cases}\bm{S}_{uu} &=& a_{11}\bm{S}_u+b_{11}\bm{S}_v+L\bm{n}\\[1em] \bm{S}_{uv} &=& a_{12}\bm{S}_u+b_{12}\bm{S}_v+M\bm{n}\\[1em]\bm{S}_{vv} &=& a_{22}\bm{S}_u+b_{22}\bm{S}_v+N\bm{n}\end{cases}\end{equation}ただし式中の6つの係数は(7)で与えられる。
定理1をガウスの公式と見なしても構いませんが、見た目が悪いので、スッキリした形にして後述します。
続いて(4)の係数を求めましょう。両辺と $\bm{S}_u$ との内積をとった式、および $\bm{S}_v$ との内積をとった式において(1)(2')を用いると\begin{equation}\begin{pmatrix}E & 0 & F & 0 \\ 0 & E & 0 & F \\ F & 0 & G & 0 \\ 0 & F & 0 & G\end{pmatrix}\begin{pmatrix}a_{1}\\a_{2}\\b_{1}\\b_{2}\end{pmatrix} =\begin{pmatrix}-L \\ -M \\ -M \\ -N\end{pmatrix}\tag{8}\end{equation}なる連立方程式を得ます。これを解くと\begin{equation}\begin{pmatrix}a_{1}\\a_{2}\\b_{1}\\b_{2}\end{pmatrix}=\frac{1}{EG-F^2}\begin{pmatrix}FM-GL\\FN-GM\\FL-EM\\FM-EN\end{pmatrix}\tag{9}\end{equation}これを(4)に代入します。第1基本行列 $\mathcal{G}$ と第2基本行列 $\mathcal{H}$ を用いれば次の定理を得ます。
単位法ベクトルの偏微分は次のように表される。\begin{equation}\begin{pmatrix}\bm{n}_u \\\bm{n}_v\end{pmatrix} = -\mathcal{HG}^{-1}\begin{pmatrix}\bm{S}_u \\\bm{S}_v\end{pmatrix}\tag{10}\end{equation}
これがワインガルテンの公式ですが、定理1と同様に少し式を書き換えます(後述)。定理1と定理2により、本記事の目標である「$\bm{S}_u$ , $\bm{S}_v$ , $\bm{n}$ の変化を $\bm{S}_u$ , $\bm{S}_v$ , $\bm{n}$ で表現」が完成しました。
第1基本行列と第2基本行列の新たな書き方として\begin{equation}\begin{pmatrix} g_{11} & g_{12} \\ g_{21} & g_{22}\end{pmatrix} :=\begin{pmatrix} E & F \\ F & G\end{pmatrix}=\mathcal{G}\tag{11}\end{equation}\begin{equation}\begin{pmatrix} h_{11} & h_{12} \\ h_{21} & h_{22}\end{pmatrix} :=\begin{pmatrix} L & M \\ M & N\end{pmatrix}=\mathcal{H}\tag{12}\end{equation}添え字にすることでより高次元の話へも拡張しやすくなります。
これまで $(u,v)$ としてきたところを $(u_1,u_2)$ と書くことにすると、第1基本量および第2基本量の定義(1)(2)より直ちに\begin{equation}g_{ij} =\dd{\bm{S}}{u_i}\cdot\dd{\bm{S}}{u_j}\;,\;h_{ij}=\frac{\partial^2\bm{S}}{\partial u_i\partial u_j}\cdot \bm{n}\quad(i,j=1,2)\tag{13}\end{equation}
これまでも見てきたように、微分幾何学には大量の偏微分が現れます。微分の記号が面倒です。よって$$\dd{A}{u_i}:=A,_{i}$$のように書くことにします。すると(13)は\begin{equation}g_{ij} =\bm{S},_i\cdot\bm{S},_j\;,\;h_{ij}=\bm{S},_{ij}\cdot\: \bm{n}\quad(i,j=1,2)\tag{14}\end{equation}$\bm{S},_{ij}$ は $i$ および $j$ で微分したことを表しています。
さらに $g_{ij}$ の上付き添え字バージョンを\begin{equation}\begin{pmatrix} g^{11} & g^{12} \\ g^{21} & g^{22}\end{pmatrix}=\begin{pmatrix} g_{11} & g_{12} \\ g_{21} & g_{22}\end{pmatrix}^{-1}=\mathcal{G}^{-1}\tag{15}\end{equation}となるように決めておきます。
さて $a_{11}=\G_{11}^{~1}$ , $b_{11}=\G_{11}^{~2}$ , $a_{12}=\G_{12}^{~1}$ , $b_{12}=\G_{12}^{~2}$ , $a_{22}=\G_{22}^{~1}$ , $b_{22}=\G_{22}^{~2}$ と書き直すと定理1は\begin{equation}\begin{cases}\bm{S},_{11} &=& \G_{11}^{~1}\bm{S},_1+\G_{11}^{~2}\bm{S},_2+h_{11}\bm{n}\\[0.5em] \bm{S},_{12} &=& \G_{12}^{~1}\bm{S},_1+\G_{12}^{~2}\bm{S},_2+h_{12}\bm{n}\\[0.5em] \bm{S},_{22} &=& \G_{22}^{~1}\bm{S},_1+\G_{22}^{~2}\bm{S},_2+h_{22}\bm{n}\end{cases}\tag{16}\end{equation}と書けます。こうするとなかなか統一感が出てきます。$\G_{ij}^{~k}$ を接続係数(クリストッフェル記号)と呼びます。(16)をもう少しまとめ、\begin{equation}\bm{S},_{ij}=\sum_{k=1}^2\G_{ij}^{~k}\:\bm{S},_k+h_{ij}\:\bm{n}\quad(i,j=1,2)\tag{17}\end{equation}とします。また $\G_{ij}^{~k}=\G_{ji}^{~k}$ です。一応ことわっておくと、ここであらわれている文字はすべて $u_1$ , $u_2$ の2変数関数です。アインシュタインの縮約記法により和記号を省略することもあります。
同様に定理2は\begin{equation}\bm{n},_{i}=-\sum_{j=1}^2\sum_{k=1}^2h_{ij}\: g^{jk}\:\bm{S},_k\quad(i=1,2)\tag{18}\end{equation}
最後に(7)を見ます。面倒くさいですが計算して確認すると\begin{equation}\G_{ij}^{~k}=\frac{1}{2}\sum_{a=1}^2g^{ka}\left(g_{ai},_{j}+g_{aj},_{i}-g_{ij},_{a}\right)\tag{19}\end{equation}が成立します。一般相対論でもおなじみです。
以上から次の結論を得ます。
接ベクトルの偏微分を接ベクトルおよび単位法ベクトルの線型結合で表した式は\begin{equation}\bm{S},_{ij}=\sum_{k=1}^2\G_{ij}^{~k}\:\bm{S},_k+h_{ij}\:\bm{n}\quad(i,j=1,2)\tag{19}\end{equation}ただし接続係数は\begin{equation}\G_{ij}^{~k}=\frac{1}{2}\sum_{a=1}^2g^{ka}\left(g_{ai},_{j}+g_{aj},_{i}-g_{ij},_{a}\right)\tag{20}\end{equation}である。
単位法ベクトルの偏微分を接ベクトルの線型結合で表した式は\begin{equation}\bm{n},_{i}=-\sum_{j=1}^2\sum_{k=1}^2h_{ij}\: g^{jk}\:\bm{S},_k\quad(i=1,2)\tag{21}\end{equation}
曲線論でいう「フレネ・セレの公式」では、曲線と曲率・捩率が対応していました。つまり関数 $\kappa(s)$ , $\tau(s)$ を与えると、それを曲率・捩率とする曲線(の形)が一意的に定まるというものです(曲線論の基本定理)。
曲面でいうと、その形を決定するのは第1基本量と第2基本量 $\{g_{ij}\}$ , $\{h_{ij}\}$ です。中内(2019)によると
$\mathcal{G}$ が正定値であるような6つの $C^\infty$ 級関数 $\{g_{ij}\}$ , $\{h_{ij}\}$ に対して、第1基本量が $g_{ij}$ で第2基本量が $h_{ij}$ であるような曲面が局所的に存在するための必要十分条件は、次の2つを満たすことである。
(1)ガウスの方程式$$\G_{jk}^{~i},_l-\G_{jl}^{~i},_k+\sum_{p=1}^2\left(\G_{jk}^{~p}\G_{pl}^{~i}-\G_{jl}^{~p}\G_{pk}^{~i}\right)=\sum_{p=1}^2(h_{jk}h_{lp}-h_{jl}h_{kp})g^{pi}$$(2)コダッチ・マイナルディの方程式$$h_{ij},_k-h_{ik},_j+\sum_{p=1}^2\left(\G_{ij}^{~p}h_{pk}-\G_{ik}^{~p}h_{pj}\right)=0$$
今回紹介した記法で、第1基本形式と第2基本形式を表すと\begin{equation}\mathrm{I}=\sum_{i=1}^2\sum_{j=1}^2 g_{ij} du^idu^j\tag{22}\end{equation}\begin{equation}\mathrm{II}=\sum_{i=1}^2\sum_{j=1}^2 h_{ij} du^idu^j\tag{23}\end{equation}事情により $du^i$ のように上の添え字としています。(13)式なども、本当はそうしたほうがいいのです。
・中内伸光『幾何学は微分しないと』
『幾何学は微分しないと』を参照しました。オヤジギャグまじりの平易な文章で微分幾何学を分かりやすく解説しています。初学者向けな分、内容はやや薄いと思うので、ネットや他の書籍を併用すると学習効果が高まります。

新装版 幾何学は微分しないと 〜微分幾何学入門〜【Amazon】
次:
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。