微分幾何学の講座・第10回。曲面のガウス曲率 $K$ は、第1基本量 $E,F,G$ のみで記述できる内在量であることを解説します。

難解なことはなくて、計算練習みたいなものだよ。
色々な量や記号を定義していますので、シリーズを通して読むとベターです。
前回はこちら:
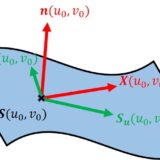
2つのパラメータ $u,v$ で表される曲面$$\bm{S}(u,v)=\bigl(x(u,v),y(u,v),z(u,v)\bigr)$$について、第1基本量は\begin{equation}E:=\bm{S}_u\cdot \bm{S}_u \;,\quad F:=\bm{S}_u\cdot \bm{S}_v\;,\quad G:=\bm{S}_v\cdot \bm{S}_v\tag{1}\end{equation}第2基本量は\begin{equation}L:=\bm{S}_{uu}\cdot \bm{n}\;,\quad M:=\bm{S}_{uv}\cdot \bm{n}\;,\quad N:=\bm{S}_{vv}\cdot \bm{n}\tag{2}\end{equation}と定義されます。$\bm{n}$ は単位法ベクトルです。
これらについては、前回記事で導入した書き方も便利です。\begin{equation}\begin{pmatrix} g_{11} & g_{12} \\ g_{21} & g_{22}\end{pmatrix} :=\begin{pmatrix} E & F \\ F & G\end{pmatrix}=\mathcal{G}\tag{3}\end{equation}\begin{equation}\begin{pmatrix} h_{11} & h_{12} \\ h_{21} & h_{22}\end{pmatrix} :=\begin{pmatrix} L & M \\ M & N\end{pmatrix}=\mathcal{H}\tag{4}\end{equation}それぞれ「第1基本行列」「第2基本行列」とよびます。
$(u,v)=(u^1,u^2)$ と書き、さらに偏微分の書き方として$$\dd{A}{u^i}:=A,_{i}\;,\quad\frac{\partial A}{\partial u^i\partial u^j}:=A,_{ij}$$を使うことがあります。
前回導出したガウスの公式は
\begin{equation}\bm{S},_{ij}=\sum_{k=1}^2\G_{ij}^{~k}\:\bm{S},_k+h_{ij}\:\bm{n}\quad(i,j=1,2)\tag{5}\end{equation}
ただし接続係数は\begin{equation}\G_{ij}^{~k}=\frac{1}{2}\sum_{a=1}^2g^{ka}\left(g_{ai},_{j}+g_{aj},_{i}-g_{ij},_{a}\right)\tag{6}\end{equation}で定義されるのでした。また、ワインガルテンの公式は
\begin{equation}\bm{n},_{i}=-\sum_{j=1}^2\sum_{k=1}^2h_{ij}\: g^{jk}\:\bm{S},_k\quad(i=1,2)\tag{7}\end{equation}
であることを解説しました。ここで現れている $g_{ij}$ の上付き添え字バージョンは\begin{equation}\begin{pmatrix} g^{11} & g^{12} \\ g^{21} & g^{22}\end{pmatrix}=\begin{pmatrix} g_{11} & g_{12} \\ g_{21} & g_{22}\end{pmatrix}^{-1}=\mathcal{G}^{-1}\tag{8}\end{equation}と定めています。
ガウス曲率は第1基本量と第2基本量を用いて\begin{equation}K=\frac{LN-M^2}{EG-F^2}\tag{9}\end{equation}であることは証明しました。一方で、これまでの知識を利用すると、$K$ の別の表し方を見つけることができます。
自明な偏微分の式$$\dd{\bm{S}_{uu}}{v}=\dd{\bm{S}_{uv}}{u}\;,\;\dd{\bm{S}_{vv}}{u}=\dd{\bm{S}_{uv}}{v}\;,\;\dd{\bm{n}_{u}}{v}=\dd{\bm{n}_{v}}{u}$$は、先ほど紹介した記法では $(u,v)=(u^1,u^2)$ として$$\dd{\bm{S},_{11}}{u^2}=\dd{\bm{S},_{12}}{u^1}\;,\;\dd{\bm{S},_{22}}{u^1}=\dd{\bm{S},_{12}}{u^2}\;,\;\dd{\bm{n},_{1}}{u^2}=\dd{\bm{n},_{2}}{u^1}$$です。左の2式に(5)を適用すると(記法は元に戻して)\begin{eqnarray}\dd{}{v}\left(\G_{11}^{~1}\bm{S}_u+\G_{11}^{~2}\bm{S}_v+L\bm{n}\right)&=&\dd{}{u}\left(\G_{12}^{~1}\bm{S}_u+\G_{12}^{~2}\bm{S}_v+M\bm{n}\right)\tag{10a}\\ \dd{}{u}\left(\G_{22}^{~1}\bm{S}_u+\G_{22}^{~2}\bm{S}_v+N\bm{n}\right)&=&\dd{}{v}\left(\G_{12}^{~1}\bm{S}_u+\G_{12}^{~2}\bm{S}_v+M\bm{n}\right)\tag{10b}\end{eqnarray}
(10a)にのみ注目します。地道に微分を実行して\begin{eqnarray*}&&\dd{\G_{11}^{~1}}{v}\bm{S}_u+\G_{11}^{~1}\bm{S}_{uv}+\dd{\G_{11}^{~2}}{v}\bm{S}_v+\G_{11}^{~2}\bm{S}_{vv}+\dd{L}{v}\bm{n}+L\bm{n}_v \\&=& \dd{\G_{12}^{~1}}{u}\bm{S}_u+\G_{12}^{~1}\bm{S}_{uu}+\dd{\G_{12}^{~2}}{u}\bm{S}_v+\G_{12}^{~2}\bm{S}_{uv}+\dd{M}{u}\bm{n}+M\bm{n}_u\end{eqnarray*}$\bm{S}$ の2階導関数と $\bm{n}$ の導関数には(5)(7)を代入します。すると\begin{eqnarray}&&\left(\dd{\G_{11}^{~1}}{v}-\dd{\G_{12}^{~1}}{u}+\G_{11}^{~2}\G_{22}^{~1}-\G_{12}^{~2}\G_{12}^{~1}+La_2-Ma_1\right)\bm{S}_u\\&&+\left(\dd{\G_{11}^{~2}}{v}-\dd{\G_{12}^{~2}}{u}+\G_{11}^{~1}\G_{12}^{~2}+\G_{11}^{~2}\G_{22}^{~2}-\G_{12}^{~1}\G_{11}^{~2}-\G_{12}^{~2}\G_{12}^{~2}+Lb_2-Mb_1\right)\bm{S}_v\\&&+\left(\G_{11}^{~1}M+\G_{11}^{~2}N+L_v-M_u-\G_{12}^{~1}L-\G_{12}^{~2}M\right)\bm{n}\\&=&0\tag{11}\end{eqnarray}ただし\begin{equation}\begin{pmatrix}a_{1}\\a_{2}\\b_{1}\\b_{2}\end{pmatrix}=\frac{1}{EG-F^2}\begin{pmatrix}FM-GL\\FN-GM\\FL-EM\\FM-EN\end{pmatrix}\tag{12}\end{equation}です((7)より現れます)。
$\bm{S}_u$ , $\bm{S}_v$ , $\bm{n}$ は線型独立ですので、(11)の $\bm{S}_u$ の係数はゼロです。これを整理すると$$K=\frac{1}{F}\left(\dd{\G_{12}^{~1}}{u}-\dd{\G_{11}^{~1}}{v}+\G_{12}^{~1}\G_{12}^{~2}-\G_{11}^{~2}\G_{22}^{~1}\right)$$となります。この過程で(9)(12)から $La_2-Ma_1=KF$ となることを用いました。
(6)から接続係数は第1基本量で定義されるので、ガウス曲率 $K$ は第1基本量とその偏微分のみで表せることが分かります。第1基本量は(1)で定義したように、接ベクトルの内積の組み合わせであり、法ベクトルは用いません。このような量を内在量といいます。すなわちガウス曲率は内在量です。これを発見した本人であるガウスも驚いて「驚異の定理」と書いたそうです。内在量だと何がすごいのかという疑問はまだ残っていますが、深く学ぶ機会があれば書くかもしれません。また、本記事のストーリーではそもそも $\bm{S}(u,v)$ を3次元ユークリッド空間内の曲面として考えていますから、曲面の外の世界を仮定していることになり、「内在」に関する議論が不足しているのではないかと思います。このあたりも、どこかで深めたいです。
ところで、(11)の $\bm{S}_v$ の係数もゼロです。これを同様に整理するとやはり $K$ の式を得ます。さらに中内(2019)では、(10a)ではなく(10b)を使って別の表式を得ています。これらより $K$ の表式として以下の3つが得られます。
\begin{eqnarray}K &=& \frac{1}{F}\left(\dd{\G_{12}^{~1}}{u}-\dd{\G_{11}^{~1}}{v}+\G_{12}^{~1}\G_{12}^{~2}-\G_{11}^{~2}\G_{22}^{~1}\right)\tag{13a} \\ K &=& \frac{1}{E}\left(\dd{\G_{11}^{~2}}{v}-\dd{\G_{12}^{~2}}{u}+\G_{11}^{~1}\G_{12}^{~2}+\G_{11}^{~2}\G_{22}^{~2}-\G_{12}^{~1}\G_{11}^{~2}-\G_{12}^{~2}\G_{12}^{~2}\right)\tag{13b} \\ K &=& \frac{1}{G}\left(\dd{\G_{22}^{~1}}{u}-\dd{\G_{12}^{~1}}{v}+\G_{11}^{~1}\G_{22}^{~1}+\G_{22}^{~1}\G_{12}^{~1}-\G_{12}^{~1}\G_{12}^{~1}-\G_{12}^{~2}\G_{22}^{~1}\right)\tag{13c}\end{eqnarray}
使い分けがあるとすると、例えば $F=0$ のときは(13a)は使えませんね。
このほかに、Weisstein, Eric W.の記事によるとBrioschi Formulaというものがあり、\begin{equation}K =\frac{M_1-M_2}{(EG-F^2)^2}\tag{14}\end{equation}ここで\begin{eqnarray*}M_1 :=&& \begin{vmatrix}-\frac{E_{vv}}{2}+F_{uv}-\frac{G_{uu}}{2} & \frac{E_u}{2} & F_u-\frac{E_v}{2} \\ F_v-\frac{G_u}{2} & E & F \\ \frac{G_v}{2} & F & G\end{vmatrix}\\ M_2 :=&&\begin{vmatrix} 0 & \frac{E_v}{2} & \frac{G_u}{2} \\ \frac{E_v}{2} & E & F \\ \frac{G_u}{2} & F & G\end{vmatrix}\end{eqnarray*}こちらも第1基本量のみで表した式であり、接続係数を計算済みである分、長くなっています。
$\mathcal{G}$ が対角行列すなわち $F=0$ の場合、$$\mathcal{G}^{-1}=\begin{pmatrix}1/E & 0 \\ 0 & 1/G\end{pmatrix}$$(6)で接続係数を計算すると\begin{eqnarray*}&&\G_{11}^{~1} = \frac{E_u}{2E} \;,\;\G_{11}^{~2} = -\frac{E_v}{2G}\\&& \G_{12}^{~1} = \frac{E_v}{2E}\;,\;\G_{12}^{~2} = \frac{G_u}{2G}\\&&\G_{22}^{~1} = -\frac{G_u}{2E}\;,\;\G_{22}^{~2} = \frac{G_v}{2G}\end{eqnarray*}(13b)に代入すると\begin{equation}K=-\frac{1}{\sqrt{EG}}\left(\dd{}{u}\frac{G_u}{\sqrt{EG}}+\dd{}{v}\frac{E_v}{\sqrt{EG}}\right)\tag{15a}\end{equation}
$(u,v)$ が(局所的に)等温パラメータであるとは$$E=G\quad,\quad F=0$$を満たすときにいいます。弧長パラメータ表示の曲面版といってもいいでしょう。曲面全体でこれを満たすのは困難ですので「局所的に」とつけておきました。この場合には(1)より$$|\bm{S}_u|=|\bm{S}_v|\quad,\quad \bm{S}_u\cdot\bm{S}_v=0$$が成立しています。接続係数を計算すると\begin{eqnarray*}&&\G_{11}^{~1} = \G_{12}^{~2} = \frac{E_u}{2E} \\ &&\G_{12}^{~1} = \G_{22}^{~2} = \frac{E_v}{2E} \\ &&\G_{11}^{~2} =- \frac{E_v}{2E}\quad,\quad \G_{22}^{~1} =-\frac{E_u}{2E}\end{eqnarray*}(13b)に代入すると\begin{equation}K =-\frac{1}{2E}\left(\frac{\partial^2}{\partial u^2}+\frac{\partial^2}{\partial v^2}\right)\ln E\tag{15b}\end{equation}が示されます。
伸縮せずに平面に展開できる曲面を可展面といいます。ペーパークラフトを思い起こすといいのですが、例えば円錐の側面(円錐面)は平面上に、扇形として展開できます。よって円錐面は可展面です。一方、球はそれができず、可展面ではありません。世界地図にはさまざまな図法がありますが、どれも伸縮を含んでいます。
3次元空間内の曲面においては\begin{equation}K=0\tag{16}\end{equation}なるものが可展面です。半径 $a$ の球は $K=a^{-2}$ なので、可展面ではないことが分かります。
柱面
平行な直線から成る曲面を「柱面」といいます。たとえば円柱の側面がそうです。今、$xy$ 平面上の曲線 $(x(u),y(u))$ に沿って、$z$ 軸に平行な直線を動かしてみましょう。これによってできる柱面は$$\bm{S}(u,v)=\bigl(x(u),y(u),v\bigr)$$と書けます(下の例1)。より一般には、空間曲線 $\bm{C}(u)$ に沿って直線を動かすので\begin{equation}\bm{S}(u,v)=\bm{C}(u)+v\bm{e}_0\tag{17}\end{equation}ここで $\bm{e}_0$ は長さ1の定ベクトルです。(17)のガウス曲率が $K=0$ となることは、(14)で $M_1=M_2=0$ となることから簡単に示せます。
ただ、接続係数の計算練習も兼ねて次の例1をやってみましょう。
放物柱面 $\bm{S}=(u,au^2,v)$ において、
(1) 第1基本行列とその逆行列を求めよ。
(2) 接続係数を求めよ。
(3) 可展面であることを示せ。

【解答】第1基本行列は$$\mathcal{G}=\begin{pmatrix} g_{11} & g_{12} \\ g_{21} & g_{22}\end{pmatrix} =\begin{pmatrix} E & F \\ F & G\end{pmatrix}=\begin{pmatrix} 1+4a^2u^2 & 0 \\ 0 & 1\end{pmatrix}$$逆行列は$$\mathcal{G}^{-1}=\begin{pmatrix} g^{11} & g^{12} \\ g^{21} & g^{22}\end{pmatrix} =\begin{pmatrix} \frac{1}{1+4a^2u^2} & 0 \\ 0 & 1\end{pmatrix}$$これらを用いて(6)を計算すると接続係数は$$\G_{11}^{~1}=\frac{4a^2u}{1+4a^2u^2}$$$$\G_{11}^{~2}=\G_{12}^{~1}=\G_{22}^{~1}=\G_{12}^{~2}=\G_{22}^{~2}=0$$(13b)に代入して $K=0$ となって可展面である。【解答終】
錐面
ある定点を通る直線を集めてできる曲面を「錐面」といいます。円錐の側面がこれにあたります。少し状況を限定すると、原点Oと、空間曲線 $\bm{C}(u)$ 上の点を結んでできる直線を集めてできる曲面は\begin{equation}\bm{S}(u,v)=v\:\bm{C}(u)\tag{18}\end{equation}面倒なので $\bm{C}(u)$ は弧長パラメータ表示であるとすると$$\mathcal{G}=\begin{pmatrix} v^2 & 0 \\ 0 & \bm{C}(u)^2\end{pmatrix}$$ここで$\bm{C}\cdot \bm{C}'=0$ に注意します。微分して $E_v=2v$ , $G_u=0$ となるので(15a)より $K=0$ となります。
円錐面 $\bm{S}=(v\cos u,v\sin u, z_0 v)$ において、
(1) 第1基本行列とその逆行列を求めよ。
(2) 接続係数を求めよ。
(3) 可展面であることを示せ。

【解答】第1基本行列とその逆行列は$$\mathcal{G}=\begin{pmatrix} v^2 & 0 \\ 0 & 1+z_0^{~2}\end{pmatrix} \;,\;\mathcal{G}^{-1}=\begin{pmatrix} 1/v^2 & 0 \\ 0 & 1/(1+z_0^{~2})\end{pmatrix}$$これらから接続係数を計算すると$$\G_{11}^{~2}=\frac{-v}{1+z_0^2}\;,\;\G_{12}^{~1}=\frac{1}{v}\;,\;\G_{ij}^{~k}=0\;(\mathrm{else})$$よってガウス曲率 $K=0$ と計算できる。【解答終】
接線曲面
定められた曲線の接線を集めて成る曲面を「接線曲面」といいます。弧長パラメータ表示された空間曲線 $\bm{C}(u)$ に対する接線曲面は\begin{equation}\bm{S}(u,v)=\bm{C}(u)+v \bm{e_1}(u)\tag{19}\end{equation}ただし $\bm{e}_1=\bm{C}'$ は単位接ベクトルです。
あえて第2基本量を使う方法で曲率を求めましょう。武器は多い方がいいです。フレネ・セレの公式も使うと、曲線の動標構 $\bm{e}_1$ , $\bm{e_2}$ , $\bm{e_3}$ によって$$\bm{S}_u=\bm{e}_1(u)+v\kappa(u)\bm{e}_2(u)\;,\;\bm{S}_v=\bm{e}_1(u)$$よって第1基本行列は$$\mathcal{G}=\begin{pmatrix} 1+v^2\kappa(u)^2 & 1 \\ 1 & 1\end{pmatrix}$$曲面の単位法ベクトルは$$\bm{n}=\frac{\bm{S}_u\times\bm{S}_v}{|\bm{S}_u\times\bm{S}_v|}=-\bm{e}_3(u)$$$$\therefore\quad\bm{n}_u=-\tau(u)\bm{e}_2(u)\;,\;\bm{n}_v=0$$これらから第2基本行列を求めると$$\mathcal{H}=\begin{pmatrix} -v\kappa(u)\tau(u) & 0 \\ 0 & 0\end{pmatrix}$$(9)より $K=0$ となって可展面です。
常螺旋 $(a\cos u,a\sin u,bu)$ の接線曲面は可展面であることを示せ。
【解答】曲面の式は$$\bm{S}=\begin{pmatrix}a\cos u-av\sin u \\ a\sin u+av\cos u \\ bu+bv\end{pmatrix}$$これより接ベクトル、接続係数を求めてもよいが、煩雑である。むしろ次のように一般に論じよう。
常螺旋の式を $\bm{C}(u)$ とする(これは弧長パラメータ表示ではない)。接触曲面は$$\bm{S}=\bm{C}(u)+v\:\bm{C}'(u)$$であるから$$\bm{S}_u=\bm{C}'+v\:\bm{C}''\;,\;\bm{S}_v=\bm{C}'\;,\;\bm{n}=\frac{\bm{C}''\times\bm{C}'}{|\bm{C}''\times\bm{C}'|}$$さらに$$\bm{S}_{uu}=\bm{C}''+v\:\bm{C}'''\;,\;\bm{S}_{uv}=\bm{C}''\;,\;\bm{S}_{vv}=0$$これらより第2基本量は$$L=\frac{v\bm{C}'''\cdot(\bm{C}''\times\bm{C}')}{|\bm{C}''\times\bm{C}'|}\;,\;M=N=0$$(9)より $K=0$【解答終】
・中内伸光『幾何学は微分しないと』
・Weisstein, Eric W. "Brioschi Formula." From MathWorld--A Wolfram Web Resource. [2023/5/3 アクセス]
『幾何学は微分しないと』を参照しました。オヤジギャグまじりの平易な文章で微分幾何学を分かりやすく解説しています。初学者向けな分、内容はやや薄いと思うので、ネットや他の書籍を併用すると学習効果が高まります。

新装版 幾何学は微分しないと 〜微分幾何学入門〜【Amazon】
お次はこちら:
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。

≪…「驚異の定理」 ・・・ 可展面…≫を、繋ぐ風景は、『ヒフミヨ ヒンメリ』のコアが創る相似形の『カタラン直角三角形』の回転体の『円錐体』(√8π/3)にあるとの記事を見つける。
数の言葉ヒフミヨ(1234)を大和言葉の【ひ・ふ・み・よ・い・む・な・や・こ・と】の平面(2次元)からの送り返して来たモノのとして十進法の基における桁表示の西洋数学の成果の符号などを纏め上げている記事を見つける。
【 結んで開いて 手を打って 結んで また開いて手を打って、その手を背伸びして重ね 】
と
このニ等辺三角形を等辺(3)底辺(2)としてグルッと一周する円錐体は、√8π/3 で、この風景こそ自然数の進む姿だ。
この三角形の『半分こ』の『カタラン直角三角形』(√8 1 3)が、1・2・3・4次元を纏めている。
1 は、π で水平な平面を創生し、
(驚異の定理)
3 は、線(1次元) 面(2次元)を縁起
(関係)付け
(『ヒフミヨ ヒンメリ』)
√8 は、水平面と垂直面を縁起(関係)付け
( i⁴=1 4次元の1 )
【 結んで開いて 手を打って 結んで また開いて手を打って、その手を背伸びして重ね 一回りしてロケットに 】
と 数の言葉ヒフミヨ(1234)を宇宙へ羽ば立たせタイ・・・