微分幾何学の講座・第5回。以降は空間にある曲面に関する様々な事項を取り上げます。今回は曲面のパラメータ表示およびそれを利用した接平面や法ベクトル、曲面の面積の表現を扱います。今後に役立つ補足としてガウス写像を紹介。
前回はこちら:
領域 $D$ で定義されるパラメータ $u,v$ を用いて、空間内の曲面は\begin{equation}\bm{S}(u,v):=\bigl(x(u,v),y(u,v),z(u,v)\bigr)\;,\quad u,v\in D\tag{1}\end{equation}と表現される。
上記ではパラメータがとりうる範囲を $D$ としています。
曲面についてはじめて学ぶ場合は、曲線からの類推が分かりやすいでしょう。空間内の曲線は1つのパラメータ(径数)によって表されるのでした。曲面の場合は2つのパラメータ(径数)によって表現できます。面は2次元だから2つの数で表すのです。
空間内に曲面があるとして、その曲面を表現するためのパラメータは、複数考えられます。これも曲線と同じですね。例えば半径1の球面は$$\bm{S}(\phi,\t):=\bigl(\cos\phi\sin\t,\sin\phi\sin\t,\cos\t\bigr)\;,\; 0\le\phi<2\pi\:,\:0\le\t\le\pi$$でもいいですし、あるいは$$\bm{S}(\phi,\t):=\bigl(\cos\phi\cos\t,\sin\phi\cos\t,\sin\t\bigr)\;,\; 0\le\phi<2\pi\:,\:-\frac{\pi}{2}\le\t\le\frac{\pi}{2}$$のみならず$$\bm{S}(\phi,\t):=\bigl(\cos2\phi\sin\t,\sin2\phi\sin\t,\cos\t\bigr)\;,\; 0\le\phi<\pi\:,\:0\le\t\le\pi$$などでも構いません。これらは確かに同一の曲面を表しますが、2つのパラメータを変化させた場合の曲面上の点の位置の変化の仕方等は異なってきます。これもやはり曲線と同じです。
楕円面は$$\bm{S}(u,v):=\bigl(a\cos u\cos v,b\cos u\sin v, c\sin u\bigr)\;,\;-\frac{\pi}{2}\le u \le\frac{\pi}{2}\:,\:0\le v<2\pi$$
$a=b=c$ のときは球面となります。
放物面は$$\bm{S}(u,v):=\bigl(au,bv, u^2+v^2\bigr)\;,\quad u,v\in\RR$$
半径 $a$ の無限に長い円柱の面は$$\bm{S}(u,v):=\bigl(a\cos u,a\sin u, v\bigr)\;,\quad 0\le u<2\pi ,v\in\RR$$
曲面上の点 $\bm{S}(u_0,v_0)$ において$$\dd{\bm{S}}{u}(u_0,v_0)\quad,\quad\dd{\bm{S}}{v}(u_0,v_0)$$の2つは曲面の接ベクトルである。
曲面に接するベクトルは無数にあります。曲面上の点のおいて曲面に接する面を考えると、その面内のベクトルはすべて曲面に接するからです。上記はそのうちの代表となる接ベクトル2本なのです。
接ベクトルは偏微分で表されています。点 $(u_0,v_0)$ において $u_0$ を固定して $v_0$ のみ動かすならば、パラメータは実質1つなので描く図形は曲線になります。$v_0$ を動かす範囲が微小であれば直線であり、接ベクトル $\dd{\bm{S}}{u}$ はこの直線に乗っています。
2つの接ベクトルは異なる方向を向いています。そうでないと $u,v$ を動かしても線になってしまい、面が作れません。なので曲面の話をするときには、この2つの接ベクトルが一次独立であることを前提としています(正則性の条件)。ただし特定の点でのみ正則性の条件を満たさないことがあり、このような点を特異点といいます。
外積の性質を思い出しましょう。2つの空間ベクトルの外積は、2つが同じ方向を向いているときにゼロとなるのでした。したがって正則性の条件は次のように書けます。
曲面上の点 $\bm{S}(u_0,v_0)$ において\begin{equation}\dd{\bm{S}}{u}(u_0,v_0)\times\dd{\bm{S}}{v}(u_0,v_0)\neq\bm{0}\tag{3}\end{equation}であれば、その点は正則である。そうでなければ特異点である。
次の例を見てみます。
$$\bm{S}(u,v)=(u^2\cos v,u^2\sin v,u^3)\;,\quad u\in\RR\:,\: 0\le v<2\pi$$なる曲面において、原点は特異点である。
これを確かめるには(3)を試せばよいです。$xy$ 平面で対称にお椀型の図形をくっつけた形をしており、原点で2つの接ベクトルがともに零ベクトルとなってしまっています。
一方、例1の楕円面は $u=\pm\frac{\pi}{2}$ すなわち $(0,0,\pm c)$ で特異点となりますが、これはパラメータの取り方によるものです。
点 $(u_0,v_0)$ と書くのは面倒なので、これを点 $P\in D$ として $\bm{S}(P)$ などのように書いてもいいことにしましょう。また $u,v$ による偏微分を $\bm{S}_u$ , $\bm{S}_v$ のように書くことにします。
曲面上の点 $\bm{S}(P)$ における任意の接ベクトルは、2つの接ベクトル $\bm{S}_u(P)$ , $\bm{S}_v(P)$ の線型結合である。接ベクトル全体を$$T_P\bm{S}=\{a\bm{S}_u(P)+b\bm{S}_v(P)|a,b\in\RR\}$$と表記する。
曲面上の点 $\bm{S}(P)$ における接平面は、2つの接ベクトル $\bm{S}_u(P)$ , $\bm{S}_v(P)$ が張る平面である。よって接平面は$$\{\bm{S}(P)+a\bm{S}_u(P)+b\bm{S}_v(P)|a,b\in\RR\}$$と表せる。
正則な点 $\bm{S}(P)$ における2つの接ベクトルは一次独立ですので、これらが張る平面を考えることができます。これを曲面の接平面とよびます。
もとの丁寧な表記に立ち返ると接ベクトル全体は$$T_{(u_0,v_0)}\bm{S}=\left\{\left. a\dd{\bm{S}}{u}(u_0,v_0)+b\dd{\bm{S}}{v}(u_0,v_0)\right|a,b\in\RR\right\}$$と書けます。
球面$$\bm{S}(u,v):=\bigl(\cos u\cos v,\cos u\sin v, \sin u\bigr)\;,\;-\frac{\pi}{2}\le u \le\frac{\pi}{2}\:,\:0\le v<2\pi$$の点 $(1,0,0)$ における接平面の方程式は $x=1$ である。
計算するまでもない例ですが、内容に沿ってやってみましょう。$(u,v)=(0,0)$ のとき $(x,y,z)=(1,0,0)$ となりますので$$\bm{S}_u(0,0)=(0,0,1)\;,\;\bm{S}_v(0,0)=(0,1,0)$$従って接平面は$$\{(1,0,0)+a(0,0,1)+b(0,1,0)|a,b\in\RR\}$$よって任意の点は$$(x,y,z)=(1,b,a)\quad,\quad a,b\in\RR$$すなわち $x=1$ です。
曲面上の点 $\bm{S}(P)$ における単位法ベクトルを次で定義する。\begin{equation}\bm{n}(P):=\frac{\bm{S}_u(P)\times\bm{S}_v(P)}{|\bm{S}_u(P)\times\bm{S}_v(P)|}\tag{4}\end{equation}
曲面上の点を始点とし、その曲面に垂直なベクトルを法ベクトルといいます。すなわち法ベクトルは前述の2つの接ベクトルに垂直というわけです。
単に法ベクトルといえば長さが任意なので、長さを1と定めて単位法ベクトル $\bm{n}$ を考えることにします。単位法ベクトルには2つの方向が考えられますが、1つに絞ってしまいましょう。$\bm{S}_u$ , $\bm{S}_v$ , $\bm{n}$ の順に右手系をなすように $\bm{n}$ をとるのです。右手系というのはその順に $x,y,z$ 軸と同じようになるということです。$x$ 方向と $y$ 方向のベクトルの外積は $z$ 方向であることと比べると、(4)のように書けることが分かります。
放物面$$\bm{S}(u,v):=\bigl(au,bv, u^2+v^2\bigr)\;,\quad u,v\in\RR$$の $(u,v)=(0,0)$ における単位法ベクトルは $(0,0,1)$ である。
単位法ベクトルを求めると$$\bm{n}(u,v)=\frac{1}{\sqrt{4b^2u^2+4a^2v^2+a^2b^2}}\begin{pmatrix}-2bu\\-2av\\ab\end{pmatrix}$$となるので直ちに導かれます。長ったらしくなるので縦ベクトルにしました。
球面$$\bm{S}(u,v):=\bigl(\cos u\cos v,\cos u\sin v, \sin u\bigr)\;,\;-\frac{\pi}{2}\le u \le\frac{\pi}{2}\:,\:0\le v<2\pi$$の単位法ベクトルは$$\bm{n}(u,v)=-(\cos u\cos v,\cos u\sin v,\sin u)=-\bm{S}(u,v)$$
$$\bm{S}_u=\begin{pmatrix}-\sin u\cos v\\-\sin u\sin v\\\cos u\end{pmatrix}\;,\;\bm{S}_v=\begin{pmatrix}-\cos u\sin v\\\cos u\cos v\\0\end{pmatrix}$$$$\bm{S}_u\times\bm{S}_v=-(\cos^2u\cos v,\cos^2u\sin v,\cos u\sin u)$$より $|\bm{S}_u\times\bm{S}_v|=|\cos u|$ となりますが、$\cos u\ge 0$ なので $|\bm{S}_u\times\bm{S}_v|=\cos u$ です。
球面上の点 $(x,y,z)$ における単位法ベクトルは$$\bm{n}=-(x,y,z)$$ということになります。
曲面上の正則な点において3つのベクトル $\bm{S}_u$ , $\bm{S}_v$ , $\bm{n}$ は基底をなします。曲線論における動標構のようなものですが、各ベクトルの長さが1とは限らないこと、$\bm{S}_u$ , $\bm{S}_v$ は一般に直交していないことの2点が異なります。パラメータの取り方によっては、任意の点において正規直交基底をつくれる可能性はありますが(等温パラメータという)、そのようなパラメータ表示を初等関数等で明示できるケースは非常に限られているので扱いません。このあたりは弧長パラメータ表示の難点と共通しています。
曲面をパラメータを用いずに\begin{equation}f(x,y,z)=0\tag{5}\end{equation}と表すこともあります。半径1の球は$$x^2+y^2+z^2-1=0$$です。例1の楕円面は$$\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}-1=0$$とも書けます。明らかにこちらのほうがスッキリしていますが、パラメータ表示が曲面上に $u$ 方向と $v$ 方向(2つの接ベクトルの方向)が定められ、いわば曲面上の座標系のようなものができあがっているのに対し、こちらはそうではありません。微分幾何学として深く学ぶにはパラメータ表示を理解しておくのがよさそうです。
ここでは(5)で表される場合の接平面と法線について、ここまでの応用として考えてみましょう。曲面 $f(x,y,z)=0$ のパラメータ表示が与えられたとすると$$f\bigl(x(u,v),y(u,v),z(u,v)\bigr)=0$$となります。$u$ で偏微分すると$$\dd{f}{u}=\dd{f}{x}\dd{x}{u}+\dd{f}{y}\dd{y}{u}+\dd{f}{z}\dd{z}{u}=0$$ナブラベクトル $\nabla=(\partial_x,\partial_y,\partial_z)$ を使うと$$\nabla f\cdot \bm{S}_u=0$$$v$ も同様に$$\nabla f\cdot \bm{S}_v=0$$よってベクトル $\nabla f$ は2つの接ベクトルに垂直なので法ベクトルです。よって曲面上の点 $(x_0,y_0,z_0)$ における法線の方程式は実数 $\lambda$ を用いて\begin{equation}(x,y,z)=(x_0,y_0,z_0)+\lambda\nabla f(x_0,y_0,z_0)\tag{6}\end{equation}と表されます。接平面上の点は$$(x-x_0,y-y_0,z-z_0)\cdot\nabla f(x_0,y_0,z_0)=0$$より接平面の方程式は\begin{equation}(x-x_0)\dd{f}{x}(x_0,y_0,z_0)+(y-y_0)\dd{f}{y}(x_0,y_0,z_0)+(z-z_0)\dd{f}{z}(x_0,y_0,z_0)=0\tag{7}\end{equation}
$u,v\in D$ が写される部分の曲面の面積は\begin{equation}S=\iint_D |\bm{S}_u\times\bm{S}_v|dudv\tag{8}\end{equation}
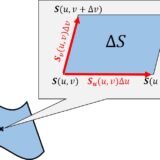
$u,v\in D$ 内の微小要素(長方形とする)は曲面上では微小な平行四辺形に写されます。これを$u,v\in D$ 全体で足し合わせれば曲面の面積となります。
曲面上の点 $\bm{S}(u,v)$ をうんと拡大して観てみましょう。$u,v$ それぞれ1次までの展開を考えると下図のように書けます。
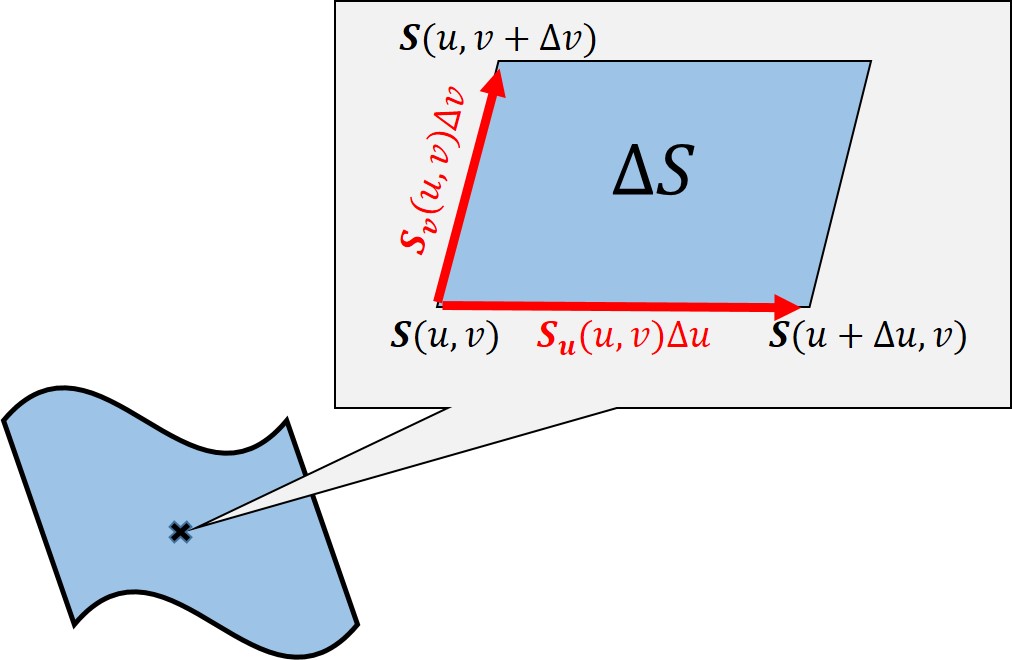
外積の大きさが平行四辺形の面積であることを思い起こせば$$\D S=|\bm{S}_u\D u\times \bm{S}_v\D v|$$$$\therefore\quad\D S=|\bm{S}_u\times\bm{S}_v|\D u\D v$$あらゆる $(u,v)\in D$ で集めると(8)を得ます。
$z=f(x,y)$ なる形で表せる曲面の $x,y\in D$ での面積は$$\iint_D\sqrt{1+f_x(x,y)^2+f_y(x,y)^2}dxdy$$である。
なぜならば、このケースの曲面は $\bm{S}(u,v)=(u,v,f(u,v))$ と定義できるので$$\bm{S}_u=(1,0,f_u)\;,\;\bm{S}_v=(0,1,f_v)$$$$\therefore\quad \bm{S}_u\times\bm{S}_v=(-f_u,-f_v,1)$$となるからです。あとは(8)の通りにやればよいです。
例7は $xy$ 平面上における $y=f(x)$ の弧長を求める式と酷似していますね。
半径1の球の表面積は $4\pi$ である。
例6Bより面積は$$\int_0^{2\pi}dv\int_{-\frac{\pi}{2}}^\frac{\pi}{2}du\cos u=2\pi\cdot 2$$より従います。
半径1の球面$$\bm{S}(u,v):=\bigl(\cos u\cos v,\cos u\sin v, \sin u\bigr)\;,\;-\frac{\pi}{2}\le u \le\frac{\pi}{2}\:,\:0\le v<2\pi$$において $u$ は緯度、$v$ は経度にあたる。$u=u_1,u_2$ の緯線および $v=v_1,v_2$ の経線で囲まれる曲面の面積は$$(v_2-v_1) (\sin u_2-\sin u_1)$$
緯度・経度といっていますが、地球のそれとは違い、単位はラジアンです。緯度の範囲が $u_1$~$u_2$ かつ経度の範囲が $v_1$~$v_2$ の範囲であるエリアの面積は$$\int_{v_1}^{v_2}dv\int_{u_1}^{u_2}du\cos u$$より従います。
曲面上の点 $\bm{S}(u,v)$ の単位法ベクトルの始点を原点に移動させると、終点は必ず単位球上へ写る。このように曲面上の点を単位球へ対応させる写像をガウス写像という。
今回は定義だけです。この定義から、写像のイメージだけしてもらえればと思います。実際に何の役に立つのかは、しばらく先のお話。
『幾何学は微分しないと』を参照しました。オヤジギャグまじりの平易な文章で微分幾何学を分かりやすく解説しています。初学者向けな分、内容はやや薄いと思うので、ネットや他の書籍を併用すると学習効果が高まります。

新装版 幾何学は微分しないと 〜微分幾何学入門〜【Amazon】
次回はこちら:
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。