微分幾何学の講座・第7回。曲面の曲がり具合を表す尺度として「法曲率」を紹介します。曲面上のある点における曲がり具合(法曲率)は、方向によって異なります。曲線に関する理論と、曲面の第1、第2基本量の知識を前提とします。
前回はこちら:
前々回はこちら:
空間内の曲面:パラメータ表示、接平面、法ベクトル、ガウス写像、面積
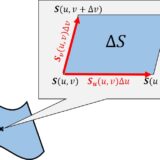
曲面は一般に2つのパラメータで表示するのでした。$$\bm{S}(u,v):=\bigl(x(u,v),y(u,v),z(u,v)\bigr)$$これを $u,v$ で偏微分するとそれぞれ $u$ , $v$ 方向の接ベクトル $\bm{S}_u$ , $\bm{S}_v$ を得ます。これらの外積をとって長さを1に規格化したものを単位法ベクトルというのでした。\begin{equation}\bm{n}(u,v):=\frac{\bm{S}_u(u,v)\times\bm{S}_v(u,v)}{|\bm{S}_u(u,v)\times\bm{S}_v(u,v)|}\tag{1}\end{equation}
曲面 $\bm{S}(u,v)$ 上の点P $=\bm{S}(u_0,v_0)$ の単位接ベクトル $\bm{X}(u_0,v_0)$ を定める。また $u$ , $v$ 方向の接ベクトル $\bm{S}_u$ , $\bm{S}_v$ とおよび単位法ベクトル $\bm{n}(u_0,v_0)$ が定まる。$\bm{X}(u_0,v_0)$ と $\bm{n}(u_0,v_0)$ が張る平面と曲面 $\bm{S}(u,v)$ の交線 $c(s)$ の(平面曲線としての)曲率 $\kappa_n(s)$ を、曲面の点Pにおける $\bm{X}$ 方向の法曲率とよぶ。ただし $s$ は弧長パラメータである。

曲面は2次元的な広がりを持ちますから、点を定めると $v(u)$ を固定したときにできる、その点を通るような $u$ 曲線($v$ 曲線)が定まります。局所的には、これらの曲線の向きは上記の接ベクトル $\bm{S}_u$ , $\bm{S}_v$ です。$\bm{S}_u$ , $\bm{S}_v$ がはる平面を接平面といい、この平面上のベクトルは全て接ベクトルです。つまり点Pにおける接ベクトルは無数にありますので、そのうちの1つを上では $\bm{X}$ としています。
曲面の点Pにおける曲がり具合は方向によって異なることは想像に難くありません。上図では何となく、$u$ 方向には曲がっていて $v$ 方向には比較的平らな感じがします。その中間くらいの方向はたぶん、中間くらいの曲がり具合なのではないか?というように。したがって法曲率は考える方向によって値が変わります。
ここでは $\bm{X}$ 方向の曲がり具合を考えることにしましょう。つまり、曲面に含まれるその方向の曲線 $c$ の曲がり具合を考えることにするのです。
曲線 $c$は1つのパラメータで表されます。そのパラメータを弧長パラメータ $s$ とすると、曲線は $\bm{c}(s)$ と書けます。
ところで、曲面は $uv$ 平面上の領域 $D$ が $\bm{S}$ によって写されたものであり、$D$ 内の曲線 $(u(s),v(s))$ は $\bm{S}$ によって、その曲面上の曲線に写されます。よって法曲率を求める際に使う曲線は\begin{equation}\bm{c}(s):=\bm{S}\bigl(u(s),v(s)\bigr)\tag{2}\end{equation}のように記述されます。ただし $s$ は $\bm{c}$ の弧長パラメータであり、$s=s_0$ で点Pに一致、つまり $(u_0,v_0)=(u(s_0),v(s_0))$ です。
さらに点Pで $\bm{X}(u_0,v_0)$ 方向を向いているので、$u(s)$ と $v(s)$ の関数形を適切に定めることにより\begin{equation}\bm{X}(u_0,v_0)=\bm{S}'\bigl(u(s_0),v(s_0)\bigr)=\bm{e}_1(s_0)\tag{2A}\end{equation}ただし $'$ は $s$ による微分です。$\bm{e}_1$ は曲線の動標構のうち、単位接ベクトルです。また上図から分かるように$$\bm{n}(u_0,v_0)=\bm{e}_2(s_0)$$と見なせます。
平面曲線における曲率は $\kappa(s)=\bm{e}_1'(s)\cdot \bm{e}_2(s)$ でした。これに倣って次のように定義します。
点 $\bm{S}(u(s),v(s))$ における法曲率を次で定義する。\begin{equation}\kappa_n(s):=\bm{S}''\bigl(u(s),v(s)\bigr)\cdot \bm{n}\bigl(u(s),v(s)\bigr)\tag{3}\end{equation}
しかし $u,v$ がどのような関数形かも分かりませんので、実際の計算はどのようにになされるか、踏み込みましょう。以下 $'$ はすべて $s$ による微分を表します。
まずチェインルールにより$$\bm{S}''=\bm{S}_{uu}(u')^2+2\bm{S}_{uv}u'v'+\bm{S}_{vv}(v')^2+\bm{S}_u u''+\bm{S}_v v''$$これを(3)に代入する際、前回の第2基本形式の定義\begin{equation}\mathrm{II}:=Ldu^2+2Mdudv+Ndv^2\tag{4}\end{equation}\begin{eqnarray}L&:=&\bm{S}_{uu}\cdot \bm{n}\tag{5a}\\ M&:=&\bm{S}_{uv}\cdot \bm{n}\tag{5b}\\ N&:=&\bm{S}_{vv}\cdot \bm{n}\tag{5c}\end{eqnarray}に注意して$$\kappa_n(s)=L(u')^2+2Mu'v'+N(v')^2+\bm{S}_u\cdot\bm{n}\:u''+\bm{S}_v\cdot\bm{n}\:v''$$接ベクトルと法ベクトルは直交するので\begin{eqnarray*}\kappa_n(s) &=& L(u')^2+2Mu'v'+N(v')^2\\ &=&\frac{Ldu^2+2Mdudv+Ndv^2}{ds^2}\end{eqnarray*}また\begin{eqnarray*}1 &=& |\bm{e}_1(s)|^2 \\&=& |\bm{S}'|^2\\&=& |\bm{S}_uu'+\bm{S}_vv'|^2\\&=&\bm{S}_u^2(u')^2+2\bm{S}_u\cdot\bm{S}_v u'v'+\bm{S}_v^2(v')^2\\ \Longrightarrow&& ds^2=Edu^2+2Fdudv+Gdv^2\end{eqnarray*} を用いて\begin{equation}\kappa_n=\frac{Ldu^2+2Mdudv+Ndv^2}{Edu^2+2Fdudv+Gdv^2}\tag{6}\end{equation}なお、第1基本形式の定義\begin{equation}\mathrm{I}:=Edu^2+2Fdudv+Gdv^2\tag{7}\end{equation}\begin{eqnarray}E&:=&\bm{S}_u\cdot \bm{S}_u\tag{8a}\\ F&:=&\bm{S}_u\cdot \bm{S}_v\tag{8b}\\ G&:=&\bm{S}_v\cdot \bm{S}_v\tag{8c}\end{eqnarray}を途中計算に用いています。
(6)の分母・分子はまさに第1基本形式・第2基本形式そのものであり、
\begin{equation}\kappa_n=\frac{\mathrm{II}}{\mathrm{I}}\tag{9}\end{equation}
あるいは行ベクトル $\sigma :=(du,dv)$、第1基本行列 $\mathcal{G}$、第2基本行列 $\mathcal{H}$ に対し\begin{equation}\kappa_n=\frac{\sigma\:\mathcal{H}\:\sigma^T}{\sigma\:\mathcal{G}\:\sigma^T}\tag{10}\end{equation}としてもいいでしょう。
曲面の式 $\bm{S}(u,v)$ が与えられたとして、(9)を実際に計算できそうでしょうか?少しハードルがあるように思うので、乗り越えるための補足を考えてみました。
基本形式が明示された(6)を見てください。$E,F,G,L,M,N$ は曲面のパラメータ表示を偏微分などの単純計算で求まる量であって特に問題ありません。問題は微小量 $du$ , $du$ です。$u,v$ がパラメータ $s$ で与えられていれば分母分子を $ds^2$ で割って\begin{equation}\kappa_n=\frac{L(u')^2+2Mu'v'+N(v')^2}{E(u')^2+2Fu'v'+G(v')^2}\tag{10}\end{equation}として計算できますが、弧長パラメータ表示すること自体がそもそも困難であることは、過去に見た通りです。
$\bm{X}$ は接ベクトルなので $\bm{S}_u$ と $\bm{S}_v$ の線型結合で表されます。具体的には(2A)より$$\bm{X}=\bm{S}_udu+\bm{S}_vdv$$つまり $\bm{X}$ の方向は $du$ と $dv$ の比で定まります。例えば $dv=0$ とおくと $\bm{X}$ は $\bm{S}_u$ の方向になります。このとき(6)は$$\kappa_n=\frac{L}{E}$$と値が分かります。
(6)で $du/dv:=p$ とすると\begin{equation}\kappa_n=\frac{Lp^2+2Mp+N}{Ep^2+2Fp+G}\tag{11}\end{equation}$p$ は $du$ と $dv$ の比であり、各点それぞれにおける方向を定めます。$p$ を動かすのに応じて法曲率も変化します。
以下、厳密といえるのか分かりませんが、具体的に法曲率を求めてみました。
半径 $a$ の球面$$\bm{S}(u,v):=\bigl(a\cos u\cos v,a\cos u\sin v, a\sin u\bigr)\;,\;-\frac{\pi}{2}\le u \le\frac{\pi}{2}\:,\:0\le v<2\pi$$の法曲率を求めよ。
前回記事より第1基本形式および第2基本形式は\begin{eqnarray*}\mathrm{I}&=&a^2du^2+a^2\cos^2udv^2\\\mathrm{II}&=& adu^2+a\cos^2udv^2\end{eqnarray*}ですので、(9)へ適用して$$\kappa_n=\frac{1}{a}$$球面上のどの点をとるかも決めず、方向にも言及していませんが、今の場合は、あらゆる点であらゆる方向に法曲率は $1/a$ ということです。
$b\ge a>0$ としたときの楕円放物面$$\bm{S}(u,v):=\bigl(au,bv, u^2+v^2\bigr)\;,\quad u,v\in\RR$$の原点における法曲率を考える。$u$ 方向と $v$ 方向の法曲率を求めよ。また、原点における法曲率の最大値と最小値を求めよ。
前回記事で第1基本形式および第2基本形式を求めました。すると$$\kappa_n=\frac{2ab du^2+2ab dv^2}{\{(a^2+4u^2)du^2+8uvdudv+(b^2+4v^2)dv^2\}\sqrt{4b^2u^2+4a^2v^2+a^2b^2}}$$$\bm{S}(u,v):=\bigl(0,0, 0\bigr)$ に対応するのは $u=v=0$ である。よって原点における法曲率は$$\kappa_n=2\frac{du^2+dv^2}{a^2du^2+b^2dv^2}$$$dv=0$ とおいたときには $u$ 方向の法曲率は $2/a^2$ と求まり、$du=0$ とおくと $v$ 方向の法曲率は $2/b^2$ と求まります。
次に $du=pdv$ とおくと$$\kappa_n=\frac{2(p^2+1)}{a^2p^2+b^2}$$これを $p^2$ の関数として、微分するなどして増減を調べると$$\frac{2}{b^2}\le \kappa_n\le \frac{2}{a^2}$$ただしこの不等式の導出には $u$ 方向の結果も用いました。
$a>0$ とする。無限に長い円柱$$\bm{S}(u,v):=\bigl(a\cos u,a\sin u, v\bigr)\;,\quad 0\le u< 2\pi\;,\;v\in\RR$$の法曲率の範囲を求めよ。
前回記事より$$\kappa_n=-\frac{adu^2}{a^2du^2+dv^2}$$式に $u,v$ が含まれないので、曲面上のどの点でも同様の法曲率になっていることが分かります。計算してみると$$-1/a\le\kappa_n\le 0$$です。法曲率 $-1/a$ は 円柱上を水平にぐるりと回る曲線(円)の曲がり具合です。法曲率 $0$ は $z$ 方向に沿った線つまり直線です。
・中内伸光『幾何学は微分しないと』
・@Phys_KM "曲面の法曲率・全曲率・平均曲率". 物理とか, 2023-04-16アクセス
『幾何学は微分しないと』を参照しました。オヤジギャグまじりの平易な文章で微分幾何学を分かりやすく解説しています。初学者向けな分、内容はやや薄いと思うので、ネットや他の書籍を併用すると学習効果が高まります。

新装版 幾何学は微分しないと 〜微分幾何学入門〜【Amazon】
次回:
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。