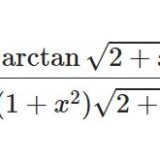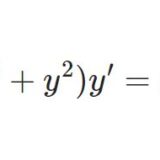前回はこちら(今回のとはほぼ無関係):
\begin{equation}\frac{dy}{dx}=y^2+x\tag{1}\end{equation}
非線型の方程式については、一部、過去記事でも取り上げています。
しかし(1)を解くには別の手立てが必要です。
関数 $f$ に対して $$L(f):=\frac{d^2f}{dx^2}-f^2$$と定めると、(1)は$$L(y)=x$$$y(x)$ をすべて左辺に、それ以外を右辺にしています。このとき、解となる関数 $f,g$ があるとすると$$L(f+g)\neq L(f)+L(g)$$ですので、この方程式は非線型です("$=$" だったら線型)。
非線型の方程式は、たとえ1階でも解けないものだらけですが、(1)は何とか(特殊関数を使って)解を得ることができます。
\begin{equation}x=\left(\frac{3}{2}t\right)^\frac{2}{3}\tag{2}\end{equation}(あるいは$t=\frac{2}{3}x^\frac{3}{2}$)と置換すると$$\frac{dy}{dx}=\left(\frac{3}{2}t\right)^\frac{1}{3}\frac{dy}{dt}$$なので(1)は次のように書けます。\begin{equation}\left(\frac{3}{2}t\right)^\frac{1}{3}\frac{dy}{dt}=y^2+\left(\frac{3}{2}t\right)^\frac{2}{3}\tag{3}\end{equation}$y(t)=\left(\frac{3}{2}t\right)^\frac{1}{3}u(t)$ と定義すると$$\frac{dy}{dt}=\left(\frac{3}{2}t\right)^\frac{1}{3}\frac{du}{dt}+\frac{1}{3}\left(\frac{3}{2t^2}\right)^\frac{1}{3}u$$これを(3)に用いて\begin{equation}\frac{du}{dt}+\frac{1}{3t}u=1+u^2\tag{4}\end{equation}
(4)では $t\to\infty$ の漸近的な解を即座に得ることができる。というのも$$\frac{du}{dt}\approx 1+u^2\quad(t\to\infty)$$より$$u(t)\approx \tan(t-t_0)$$
(4)において\begin{equation}v(t)=\exp\left(-\int u(t)dt\right)\tag{5a}\end{equation}と置きます。すなわち\begin{equation}u=-\frac{v'}{v}\tag{5b}\end{equation}ということです。
(5a)は不定積分を含むため、$v$ には定数倍の不定性が生じています。しかし(5b)を見ると分かるように $u$ に直すときは分母分子で相殺します。頭の隅に入れておきましょう。
さて、これにより\begin{equation}v''+\frac{1}{3t}v'+v=0\tag{6}\end{equation}と2階線型微分方程式になりました。
(6)はフロベニウス法によって級数解が求まる典型例です。しかしここまで天下り的な変数変換を多用してきたので、またしても\begin{equation}v(t)=t^\frac{1}{3}w(t)\tag{7}\end{equation}と置きなおしましょう。すると\begin{equation}t^2w''+tw'+\left(t^2-\frac{1}{9}\right)w=0\tag{8}\end{equation}これはベッセルの微分方程式です。非常によく知られた方程式で、たいていの場合は解を初等関数で表現できません。(8)は $\nu=1/3$ で非整数なので2つの線型独立な特殊解は\begin{equation}w_1=J_{\frac{1}{3}}(t)\quad,\quad w_2=J_{-\frac{1}{3}}(t)\tag{9}\end{equation}よって一般解は\begin{equation}w(t)=aJ_{\frac{1}{3}}(t)+bJ_{-\frac{1}{3}}(t)\tag{10}\end{equation}
(10)の段階で任意定数は $a,b$ の2つです。もともとの方程式(1)は1階なので任意定数は1つのはずです。これは先ほど説明した $v$ の定数倍の不定性によります。一応、意識しておきましょう。
ここから $y(x)$ の形での一般解へ変換していきます。単調な計算が続きます。まず(7)から\begin{equation}v(t)=t^\frac{1}{3}\left(aJ_{\frac{1}{3}}(t)+bJ_{-\frac{1}{3}}(t)\right)\tag{11}\end{equation}(11)を微分しておいて(5b)より\begin{equation}u(t)=-\frac{a\left(t^\frac{1}{3}J_{\frac{1}{3}}(t)\right)'+b\left(t^\frac{1}{3}J_{-\frac{1}{3}}(t)\right)'}{t^\frac{1}{3}\left(aJ_{\frac{1}{3}}(t)+bJ_{-\frac{1}{3}}(t)\right)}\tag{12}\end{equation}ベッセルの微分方程式で示した公式\begin{align}\frac{d}{dx}(x^\nu J_\nu)&=x^\nu J_{\nu-1}\tag{13a}\\\frac{d}{dx}(x^{-\nu} J_\nu)&=-x^{-\nu} J_{\nu+1}\tag{13b}\\J_{\nu+1}+J_{\nu-1}&=\frac{2\nu}{x}J_\nu\tag{13c}\\J_{\nu-1}-J_{\nu+1}&=2{J_\nu}'\tag{13d}\end{align}を利用して(12)の微分を実行します。方針としてはベッセル関数 $J_\nu(t)$ について $|\nu|<1$ のみを含む式にするのです。すると\begin{equation}u(t)=\frac{bJ_{\frac{2}{3}}(t)-aJ_{-\frac{2}{3}}(t)}{aJ_{\frac{1}{3}}(t)+bJ_{-\frac{1}{3}}(t)}\tag{14}\end{equation}$a$ で約分します。$c=b/a$ として\begin{equation}u(t)=\frac{cJ_{\frac{2}{3}}(t)-J_{-\frac{2}{3}}(t)}{J_{\frac{1}{3}}(t)+cJ_{-\frac{1}{3}}(t)}\tag{15}\end{equation}ただし $a=0$ の場合もあるので、$c=\infty$ を対応させます。ここで任意定数が1つ減ってめでたしめでたし。
(15)を微分して(13)を利用して計算すると(4)が成立しましたので、ここまで合っているようです。
$y(t)=\left(\frac{3}{2}t\right)^\frac{1}{3}u(t)$ でしたから\begin{equation}y(t)=\left(\frac{3}{2}t\right)^\frac{1}{3}\frac{cJ_{\frac{2}{3}}(t)-J_{-\frac{2}{3}}(t)}{J_{\frac{1}{3}}(t)+cJ_{-\frac{1}{3}}(t)}\tag{16}\end{equation}$t=\frac{2}{3}x^\frac{3}{2}$ なので最終的に
方程式(1)の解は\begin{equation}y=\sqrt{x}\frac{cJ_{\frac{2}{3}}(\frac{2}{3}x^\frac{3}{2})-J_{-\frac{2}{3}}(\frac{2}{3}x^\frac{3}{2})}{J_{\frac{1}{3}}(\frac{2}{3}x^\frac{3}{2})+cJ_{-\frac{1}{3}}(\frac{2}{3}x^\frac{3}{2})}\tag{17}\end{equation}
です!
今回解いた方程式はRiccati型とよばれるものの1つです。より一般的な解法は各文献で多く取り上げられています。
$$y'+y^2=0$$を解け。(5b)と似た変換をするとよい。
$y=u'/u$ とすると $u''=0$ を得ます。よって$$y(x)=\frac{1}{x-c}$$$c$ は任意定数ですので、解の特異点が動くということです。これは線型方程式には見られないことです。
非線型の方程式$$xy''+2(xy+1)y'+2y^2+2=0$$において $u=y^2+y'$ なる変換により1階線型方程式$$xu'+2u+2=0$$に帰着することを確認せよ。
今回 [1] を読んだ範囲で気になるものをメモ。いずれ取り組むかも。⇒取り組みました。
\begin{equation}(x^2+y^2)y'=xy\tag{A}\end{equation}の一般解は陰関数の形で次のように書ける。\begin{equation}2y^2\ln(cy)-x^2=0\tag{B}\end{equation}
\begin{equation}\left\{(y')^2+1\right\}^3=r^2(y'')^2\tag{C}\end{equation}の解は\begin{equation}(x-a)^2+(y-b)^2=r^2\tag{D}\end{equation}なる一般解および $y=\pm ix$ なる特異解からなる。
\begin{equation}xyy''=yy'+xy'^2\tag{E}\end{equation}の一般解は\begin{equation}y=Ae^{Bx^2}\tag{F}\end{equation}
次回はこちら:
[1] H.T.Davis (1960), Introduction to nonlinear differential and integral equations, U.S. Atomic Energy Commission
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。