ベッセルの微分方程式をフロベニウス法により解く．代表的な特殊解は第1種ベッセル関数と第2種ベッセル関数である．後半の例題では異なる形の方程式が，適切な変数変換によりベッセルの微分方程式に帰着する多様な例を見ることができる．漸化式や初等関数となる例も示す．
\begin{equation}x^2y^{\prime\prime}+xy'+(x^2-\nu^2)y=0 \quad (\nu \in \mathbb{R})\tag{1}\end{equation}
初等的に解くことはできませんので級数解を求めます．$x=0$ で正則でないのでフロベニウス法を用いましょう．
フロベニウス法については
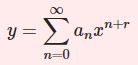【D11】級数法・フロベニウス法
を参照ください．
もくじ
$$y(x)=\sum^\infty_{m=0}a_mx^{m+r}\;,\;a_0\ne 0$$とおき，微分方程式(1)に代入します．\begin{eqnarray*}&&x^2y^{\prime\prime}+xy'+(x^2-\nu^2)y=0\\&\Leftrightarrow& \sum^\infty_{m=0}(m+r)(m+r-1)a_mx^{m+r}+\sum^\infty_{m=0}(m+r)a_mx^{m+r}+(x^2-\nu^2)\sum^\infty_{m=0}a_mx^{m+r}=0 \\&\Leftrightarrow& \sum^\infty_{m=0}\{(m+r)(m+r-1)+(m+r)-\nu^2\}a_mx^m+ \sum^\infty_{m=2}a_{m-2}x^m=0\\&\Leftrightarrow& (r^2-\nu^2)a_0+(1+r+\nu)(1+r-\nu)a_1x+\sum^\infty_{m=2}\{(m+r+\nu)(m+r-\nu)a_m+a_{m-2}\}x^m=0\end{eqnarray*}第1項に注目します．決定方程式は $a_0\ne 0$ より $r^2-\nu^2=0$ で，その解は $r=\pm\nu$ です．それぞれの $r$ について求めた級数が特殊解になります．なお(1)の形からして $\nu\ge 0$ として一般性を失いません．
$\nu\notin \mathbb{Z}$ とします．$r=\nu \geq 0$ のほうから考えます．級数を代入した微分方程式は$$(1+2\nu)a_1x+\sum^\infty_{m=0}\{m(m+2\nu)a_m+a_{m-2}\}x^m=0$$これが恒等的に成り立つことにより得られる漸化式は$$\begin{cases}a_0= 任意\\a_1=0\\m(m+2\nu)a_m+a_{m-2}=0\end{cases}$$よって奇数項はすべて$0$であり，偶数項のみ考えればよいです．\begin{eqnarray*}a_{2m}&=&-\frac{1}{2m(2m+2\nu)}a_{2m-2}\\&\vdots &\\&=&\left(-\frac{1}{4}\right)^m\frac{\Gamma(\nu+1)}{m! \Gamma(m+\nu+1)}a_0\end{eqnarray*}$a_0=\displaystyle\frac{1}{2^\nu \Gamma(\nu+1)}$ とすると$$a_{2m}=\left(-\frac{1}{4}\right)^m\frac{1}{2^\nu m!\Gamma(m+\nu+1)}$$これによって特殊解の1つ\begin{equation}J_\nu(x) = \sum^\infty_{m=0}\frac{(-1)^m}{2^{2m+\nu}m! \Gamma(m+\nu+1)}x^{2m+\nu}\tag{2}\end{equation}が求まります．$J_\nu(x)$ を第1種ベッセル関数といいます。$\nu$ は微分方程式(1)において $\nu^2$ としてあらわれているため，$r=-\nu$とした場合も同時に解ですから，そのときの特殊解は\begin{equation}J_{-\nu}(x) =\sum^\infty_{m=0}\frac{(-1)^m}{2^{2m-\nu}m! \Gamma(m-\nu+1)}x^{2m-\nu}\tag{3}\end{equation}です．
よって $J_\nu(x)$ と $J_{-\nu}(x)$ の２つの特殊解を得ることができました．これらは独立であり，一般解は即座に$$y(x)=c_1J_\nu(x) +c_2 J_{-\nu}(x)$$とできます．
$\nu$ が非負整数 $n$ であるとします．決定方程式の解は $r=\pm n$ です．$r=n$ のときは(2)そのままの式 $J_n(x)$ が特殊解となります．\begin{equation}J_n(x)= \sum^\infty_{m=0}\frac{(-1)^m}{2^{2m+n}m!(m+n)!}x^{2m+n}\tag{4}\end{equation}
$r=-n$ のときは漸化式$$\begin{cases}a_0= 任意\\a_1=0\\m(m-2n)a_m+a_{m-2}=0\end{cases}$$ を得ます．奇数項はすべてゼロになるので 偶数項についての漸化式$$ 2m(2m-2n)a_{2m}+a_{2m-2}=0 $$を考えます．$m=n$ としてみると $a_{2n-2}=0$ となります．よって漸化式を繰り返し用いることにより$$a_0=a_2=\cdots=a_{2n-2}=0$$となりますので $a_{2n}$ が任意の数で開始項となります．(3)と一致するようにとれば$$ J_{-n}(x) =\sum^\infty_{m=n}\frac{(-1)^m}{2^{2m-n}m! (m-n)!}x^{2m-n} $$$m=n$ スタートであることに注意．これを変形していくと\begin{eqnarray*}J_{-n}(x)&=& \sum^\infty_{m=0}\frac{(-1)^{m+n}}{2^{2m+n}(m+n)! m!}x^{2m+n}\\&=& (-1)^n\sum^\infty_{m=0}\frac{(-1)^m}{2^{2m+n}(m+n)! m!}x^{2m+n}\\&=&(-1)^nJ_n(x)\end{eqnarray*}よって $J_n(x)$ と $J_{-n}(x)$ は一次従属です． この２つの特殊解は一般解を与えないことになります．
では $\nu\in\mathbb{Z}$ のときの一般解はどうすればいいのでしょう．
まず $\nu=0$ で考えます．\begin{equation}xy^{\prime\prime}+y'+xy=0\end{equation}フロベニウス法によって得られる $J_0(x)$ が1つ目の特殊解になります．よって\begin{equation}xJ^{\prime\prime}_0+J'_0+xJ_0=0\end{equation}が成り立ちます．ここまでは今までと変わりありません．
ここで第2の特殊解の試行解として$$y_2=J_0(x)\ln x+\sum^\infty_{m=1}A_mx^m$$と置き，微分方程式に代入してみると$$(xJ^{\prime\prime}_0+J'_0+xJ_0)\ln x+2J_0'+\sum^\infty_{m=1}m^2A_mx^{m-1}+\sum^\infty_{m=3}A_{m-2}x^{m-1}=0$$第1項は消えて$$2J_0'+\sum^\infty_{m=1}m^2A_mx^{m-1}+\sum^\infty_{m=3}A_{m-2}x^{m-1}=0$$これに第1種ベッセル関数の式$$J_0(x) = \sum^\infty_{m=0}\frac{(-1)^m}{2^{2m}m! m!}x^{2m}$$を代入すると$$\sum^\infty_{m=1}\frac{(-1)^m}{2^{2m-2}m! (m-1)!}x^{2m-1}+\sum^\infty_{m=1}m^2A_mx^{m-1}+\sum^\infty_{m=3}A_{m-2}x^{m-1}=0$$シグマを書き下して次数の低いほうから調べていくと、
- 定数項から $A_1=0$
- 1次の項から $4A_2-1=0$
- $x^{2k}$ の項から $(2k+1)^2A_{2k+1}+A_{2k-1}=0\;(k\ge1 )$
- $x^{2k-1}$ の項から$$\frac{(-1)^k}{2^{2k-2}k!(k-1)!}+4k^2A_{2k}+A_{2k-2}=0\;(k\ge 2)$$
よって以下の関係式を得ます。$$\begin{cases}A_1=A_3=A_5=\cdots =0 \\A_2=\displaystyle\frac{1}{4}\\A_{2k}=\left(-\displaystyle\frac{1}{4k^2}\right)\left[ A_{2k-2}+\displaystyle\frac{(-1)^k}{2^{2k-2}k!(k-1)!}\right]\quad (k\geq 2)\end{cases}$$偶数項の漸化式は解けて$$A_{2k}=\frac{(-1)^{k-1}}{2^{2k}(k!)^2}h_k \quad , \quad h_k=1+\frac{1}{2}+\cdots \frac{1}{k}$$となります（数学的帰納法で簡単に確認できます）．よって第2の特殊解は$$y_2=J_0(x)\ln x-\sum^\infty_{m=1}\frac{(-1)^mh_m}{2^{2m}(m!)^2}x^{2m}$$解の基底は $J_0$ とこの $y_2$ としてもよいのですが、$y_2$ を $\displaystyle\frac{2}{\pi}(y_2+(\gamma-\ln 2)J_0)$ におきかえて基底としたものを０次の第２種ベッセル関数 $Y_0(x)$ とよび，$$Y_0(x)=\frac{2}{\pi}\left[ J_0(x)\left(\ln\frac{x}{2}+\gamma \right)- \sum^\infty_{m=1}\frac{(-1)^mh_m}{2^{2m}(m!)^2}x^{2m} \right]$$となります。$\gamma$ はオイラー・マスケローニ定数です。
よって $\nu=0$ のベッセルの微分方程式の一般解は$$y=c_1J_0(x)+c_2Y_0(x)$$と表せることが分かります．第1種ベッセル関数と第2種ベッセル関数の線型結合が一般解となるわけです．
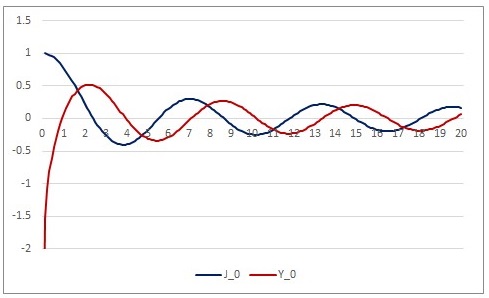
なお一般の $n$ における第2種ベッセル関数 $Y_n(x)$ は$$Y_n(x)=\frac{2}{\pi}J_n(x)\left(\ln\frac{x}{2}+\gamma\right)-\frac{x^n}{\pi}\sum^\infty_{m=0}\frac{(-1)^m(h_m+h_{m+n})}{2^{2m+n}m!(m+n!)}x^{2m}-\frac{x^{-n}}{\pi}\sum^{n-1}_{m=0}\frac{(n-m-1)!}{2^{2m-n}m!}x^{2m}$$となります．これの導出については：
一般の $\nu\in\mathbb{R}$ における第2種ベッセル関数は$$\begin{cases}Y_\nu(x)=\displaystyle\frac{1}{\sin\nu\pi}[J_\nu(x)\cos\nu\pi-J_{-\nu}(x)]\\Y_n(x)=\displaystyle\lim_{\nu\to n}Y_\nu(x)\end{cases}$$$\nu \notin \mathbb{Z}$ のときは解の基底を $J_\nu , J_{-\nu}$ としてきましたが、$Y_\nu$ がそれらの線型結合になっているので基底を $Y_\nu ,J_\nu$ に取り換えても構いませんよね．このようにすることで $\nu \in \mathbb{Z}$ では $Y_\nu$ は $\nu\to n$ の極限値で求まるようになっています．
以上からベッセルの微分方程式の一般解は$$y(x)=c_1J_\nu(x)+c_2Y_\nu(x)$$となるのです．
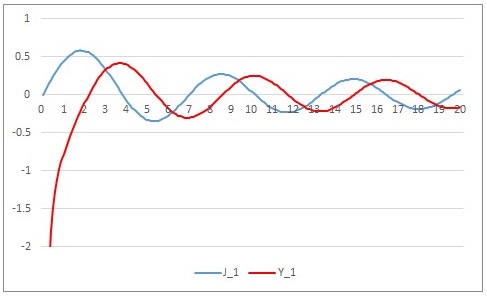
$$x^\nu J_\nu=\sum^\infty_{m=0}\frac{(-1)^m}{2^{2m+\nu}m!\Gamma(m+\nu+1)}x^{2m+2\nu}$$を微分すると$$\frac{d}{dx}(x^\nu J_\nu)=\sum^\infty_{m=0}\frac{(-1)^m\cdot 2(m+\nu)}{2^{2m+\nu}m! \Gamma(m+\nu+1)}x^{2m+2\nu-1}=x^\nu J_{\nu-1}$$$$\therefore \frac{d}{dx}(x^\nu J_\nu)=x^\nu J_{\nu-1}$$同様にして$$\frac{d}{dx}(x^{-\nu} J_\nu)=-x^{-\nu} J_{\nu+1}$$あらわれた2式をそれぞれ微分して$$\begin{cases}\nu x^{\nu-1}J_\nu +x^\nu {J_\nu}'=x^\nu J_{\nu-1} \\-\nu x^{-\nu-1}J_\nu +x^{-\nu} {J_\nu}'=-x^{-\nu} J_{\nu+1}\end{cases}$$この2式から${J_\nu}'$を消去あるいは$J_\nu$を消去することで$$J_{\nu+1}+J_{\nu-1}=\frac{2\nu}{x}J_\nu$$$$J_{\nu-1}-J_{\nu+1}=2{J_\nu}'$$なる漸化式を得ます．
第1種ベッセル関数 $J_\nu$ は特殊関数であり，一般には初等関数で表せません．しかし $\nu$ が半整数値の場合は特別です．第1種ベッセル関数の式$$J_\nu(x) = \sum^\infty_{m=0}\frac{(-1)^m}{2^{2m+\nu}m! \Gamma(m+\nu+1)}x^{2m+\nu}$$より\begin{eqnarray*}J_{1/2}(x)&=&\sqrt{x}\sum^\infty_{m=0}\frac{(-1)^m x^{2m}}{2^{2m+1/2}m!\Gamma(m+3/2)}\\ &=&\frac{1}{\sqrt{x}}\sum^\infty_{m=0}\frac{(-1)^m x^{2m+1}}{2^{2m+1/2}m!\Gamma(m+3/2)}\\ &=&\frac{1}{\sqrt{x}}\sum^\infty_{m=0}\frac{(-1)^m x^{2m+1}}{2^{2m+1/2}m!(m+1/2)(m-1/2)\cdots 1/2\Gamma(1/2)}\\ &=&\sqrt{\frac{2}{\pi x}}\sum^\infty_{m=0}\frac{(-1)^m x^{2m+1}}{2^{2m+1}m!(m+1/2)(m-1/2)\cdots 1/2}\\ &=& \sqrt{\frac{2}{\pi x}}\sum^\infty_{m=0}\frac{(-1)^m x^{2m+1}}{(2m)!!(2m+1)!!}\\ &=& \sqrt{\frac{2}{\pi x}}\sum^\infty_{m=0}\frac{(-1)^m x^{2m+1}}{(2m+1)!}\\ &=&\sqrt{\frac{2}{\pi x}}\sin x\end{eqnarray*}と計算でき，初等関数だと分かります．
漸化式 $(x^{1/2}J_{1/2})'=x^{1/2}J_{-1/2}$ を利用して$$J_{-1/2}(x)=\sqrt{\frac{2}{\pi x}}\cos x$$さらに3項間漸化式$$J_{\nu+1}+J_{\nu-1}=\frac{2\nu}{x}J_\nu$$を用いれば $J_{3/2}$ も初等関数であり，繰り返し漸化式を使うことで $\nu=\pm \displaystyle\frac{1}{2} , \pm\frac{3}{2},\cdots$ で $J_\nu$ は初等函数であらわせることが分かります．
$$x^2y^{\prime\prime}+xy'+\left(x^2-\displaystyle\frac{1}{9}\right)y=0$$
$\nu=1/3$ より第1種ベッセル関数が一般解を与えます．$$y=c_1J_{1/3}(x)+c_2J_{-1/3}(x)$$もちろん第2項を $Y_{1/3}(x)$ としてもOK．
$$x^2y^{\prime\prime}+xy'+(a^2x^2-\nu^2)y=0\;(\nu\notin\mathbb{Z})$$
$ax=z$ とおくと$$\frac{dy}{dx}=a\frac{dy}{dz}\;,\;\frac{d^2y}{dx^2}=a^2\frac{d^2y}{dz^2}$$代入して整理すると$$z^2\frac{d^2y}{dz^2}+z\frac{dy}{dz}+(z^2-\nu^2)y=0$$$\nu\notin\mathbb{Z}$ よりベッセル関数が一般解を与えます。$$y=c_1J_\nu(ax)+c_2J_{-\nu}(ax)$$
$$x^2y^{\prime\prime}+xy'+\left(4x^4-\displaystyle\frac{1}{4}\right)y=0$$
$x^2=z$ とおくと $$y'=2\sqrt{z}\frac{dy}{dz}\;,\;y^{\prime\prime}=4z\frac{d^2y}{dz^2}+2\frac{dy}{dz}$$微分方程式に代入して整理すると$$z^2\frac{d^2y}{dz^2}+z\frac{dy}{dz}+\left(z^2-\displaystyle\frac{1}{16}\right)y=0$$$\nu\notin\mathbb{Z}$ よりベッセル関数が一般解を与えます．$$y=c_1J_{1/4}(x^2)+c_2J_{-1/4}(x^2)$$
$xy^{\prime\prime}+5y'+xy=0$ の特殊解を１つ求めよ。
$u(x)=x^2y$ とおくと$$y'=\frac{1}{x^2}u'-\frac{2}{x^3}u$$$$y^{\prime\prime}=\frac{6}{x^4}u-\frac{4}{x^3}u'+\frac{1}{x^2}u^{\prime\prime}$$微分方程式に代入して整理すると$$x^2u^{\prime\prime}+xu'+(x^2-4)=0$$よって特殊解は $u(x)=J_{2}(x)$ ですので$$y_1=\frac{1}{x^2}J_{2}(x)$$
$$x^2y^{\prime\prime}+\displaystyle\frac{1}{4}\left(x+\frac{3}{4}\right)y=0$$
$y=u(x)\sqrt{x}\;,\;\sqrt{x}=z$ と変換すると$$z^2\frac{d^2u}{dz^2}+z\frac{du}{dz}+\left(z^2-\frac{1}{4}\right)u=0$$よって$$u(z)=aJ_{1/2}(z)+bJ_{-1/2}(z)$$ここで$$J_\nu(x) = x^\nu\sum^\infty_{m=0}\frac{(-1)^m}{2^{2m+\nu}m! \Gamma(m+\nu+1)}x^{2m}$$$$J_{-\nu}(x) = x^{-\nu} \sum^\infty_{m=0}\frac{(-1)^m}{2^{2m-\nu}m! \Gamma(m-\nu+1)}x^{2m}$$より級数を計算すると$$J_{1/2}(z)\propto\frac{\sin z}{\sqrt{z}}\;,\;J_{-1/2}(z)\propto\frac{\cos z}{\sqrt{z}}$$となりますので$$u(z)=c_1\frac{\sin z}{\sqrt{z}}+c_2\frac{\sin z}{\sqrt{z}}$$$$\therefore\quad y(x)=x^{\frac{1}{4}}(c_1\sin\sqrt{x}+c_2\cos\sqrt{x})$$
$I=\displaystyle\int^2_1x^{-3}J_4(x)dx$ を計算せよ．$J_0$ , $J_1$ を解答に含めてよい．
$x^{-3}J_4=-(x^{-3}J_3)'$ より$$I=-\int^2_1(x^{-3}J_3)'dx=-\left[ \frac{J_3(x)}{x^3}\right]^2_1$$となります．ここで$$J_3+J_1=\frac{4}{x}J_2 \Longleftrightarrow J_3=\frac{4}{x}J_2-J_1$$$$J_2+J_0=\frac{2}{x}J_1 \Longleftrightarrow J_2=\frac{2}{x}J_1-J_0$$より$$J_3=\left( \frac{8}{x^2}-1 \right)J_1-\frac{4}{x}J_0$$$$\therefore I=-\frac{1}{8}J_1(2)+\frac{1}{4}J_0(2)+7J_1(1)-4J_0(1)$$
$\displaystyle\frac{d}{dx}(x^\nu J_\nu)=x^\nu J_{\nu-1}\; ,\; \displaystyle\frac{d}{dx}(x^{-\nu} J_\nu)=-x^{-\nu} J_{\nu+1}$ の2式からベッセル微分方程式を導け．
$$\begin{cases}J_{\nu-1}=x^{-\nu}\displaystyle\frac{d}{dx}(x^\nu J_\nu)\\\displaystyle\frac{d}{dx}(x^{-\nu+1} J_{\nu-1})=-x^{-\nu+1}J_{\nu}\end{cases}$$$J_{\nu-1}$を下の式へ代入すれば，\begin{eqnarray*}&&\frac{d}{dx}\left[ x^{-\nu+1} x^{-\nu}\displaystyle\frac{d}{dx}(x^\nu J_\nu)\right]=-x^{-\nu+1} J_{\nu}\\&\Leftrightarrow& \frac{d}{dx}\left[x^{-2\nu+1}(\nu x^{\nu-1}J_\nu+x^\nu J'_\nu)\right]=-x^{-\nu+1} J_{\nu}\\&\Leftrightarrow& x^2J^{\prime\prime}_\nu+xJ'_\nu+(x^2-\nu^2)J_\nu=0\end{eqnarray*}これはまさにベッセルの微分方程式です．
一般の斉次2階線型常微分方程式 $y^{\prime\prime}+p(x)y'+q(x)y=0$ において $y=u(x)v(x)$ としたときに $u'$ を含まないような微分方程式を得たいとします．代入すると$$u^{\prime\prime}v+(2v'+pv)u'+(v^{\prime\prime}+pv')u+quv=0$$$u'$ の項をなくすには $2v'+pv=0$ すなわち$$v(x)=\exp \left(-\frac{1}{2}\int p(x)dx\right)$$とおけばよいことになります．
ベッセルの微分方程式において応用してみましょう．$$x^2y^{\prime\prime}+xy'+(x^2-\nu^2)y=0$$を$$y^{\prime\prime}+\frac{1}{x}y'+\left(1-\frac{\nu^2}{x^2}\right)y=0$$と変形して$$v(x)\equiv\exp \left(-\frac{1}{2}\int \frac{1}{x}dx\right)=\frac{1}{\sqrt{x}}$$とおきます．$y=u(x)\displaystyle\frac{1}{\sqrt{x}}$ とおいてベッセル方程式に代入すると1階微分がない方程式
$$x^2u^{\prime\prime}+\left(x^2+\frac{1}{4}-\nu^2\right)u=0$$
を得ます．
例題をやってみましょう．
$\nu=1/2$ についてのベッセルの微分方程式を上の方法で解け．
$y=u(x)\displaystyle\frac{1}{\sqrt{x}}$ として1階導関数を消去すると$$u^{\prime\prime}+u=0$$すなわち $u(x)=c_1\sin x+c_2\cos x$ です．よって解は$$y=c_1\frac{\sin x}{\sqrt{x}}+c_2\frac{\cos x}{\sqrt{x}}$$
物理学でベッセルの微分方程式はときどき現れます．参考記事は以下です．
第1種ベッセル関数の積分表示についての記事は
ベッセルの微分方程式の非斉次解についてはこちら：
Anger関数とWeber関数②(ベッセル微分方程式の非斉次解)
本記事では、下記の本を大いに参考にしています。厳密性はほどほどに、なるべくたくさんの演習問題が用意されています。産業や自然界における事例も豊富。数学科以外の理学部・工学部生にオススメです。
【Amazon】常微分方程式 (技術者のための高等数学)
次回の記事：
常微分方程式シリーズ
Please support me!
記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。
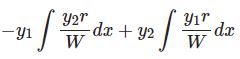
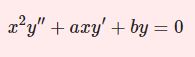
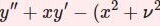
決定方程式を導く、の項の、最後のシグマはm=2ではありませんか？
ありがとうございます。訂正しました。何か見つけたらまたいつでもお願いします。