$a,b>0$,$$\int_0^\infty\frac{\cos ax-e^{-ax}}{x(x^4+b^4)}dx=\frac{\pi }{2b^4}e^{-\frac{ab}{\sqrt{2}}}\sin\frac{ab}{\sqrt{2}}$$$$\int_0^\infty\frac{\sin ax}{x(x^4+b^4)}dx=\frac{\pi}{2b^4}\left(1-e^{-\frac{ab}{\sqrt{2}}}\cos\frac{ab}{\sqrt{2}}\right)$$
いかにも複素積分って感じの式ですが、$\cos x$ と $e^{-x}$ が混じっています。これは $e^{iz}$ において $z$ が実軸上のときと虚軸上のときにそれぞれ対応していると考えられますので、次の複素関数と経路 $C$ を考えます。
$$f(z)=\frac{e^{iaz}}{z(z^4+b^4)}$$
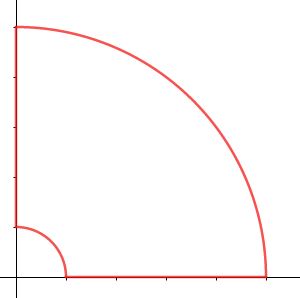
大きな半径 $R$ の円弧を $\G_R$, 小さな半径 $\epsilon$ の円弧を $\G_\epsilon$ とします。この経路内部には $f(z)$ の1位の極(pole) $z=be^{\frac{\pi}{4}i}$ があります。よって留数定理(residue)よりこの周回積分は\begin{eqnarray*}2\pi i\mathrm{Res}f(z)&&=\int_0^\infty\frac{e^{iax}}{x(x^4+b^4)}dx+\int_{\G_R}\frac{e^{iaz}}{z(z^4+b^4)}dz\\&&\quad+\int_\infty^0\frac{e^{ia(ix)}}{ix((ix)^4+b^4)}idx+\int_{\G_\epsilon}\frac{e^{iaz}}{z(z^4+b^4)}dz\\&&=\int_0^\infty\frac{\cos ax+i\sin ax}{x(x^4+b^4)}dx+\int_{\G_R}\frac{e^{iaz}}{z(z^4+b^4)}dz\\&&\quad-\int^\infty_0\frac{e^{-ax}}{x(x^4+b^4)}dx+\int_{\G_\epsilon}\frac{e^{iaz}}{z(z^4+b^4)}dz\end{eqnarray*}したがって次のように整理できます。\begin{eqnarray}2\pi i\mathrm{Res}f(z)&&=\int_0^\infty\frac{\cos ax-e^{-ax}}{x(x^4+b^4)}dx+i\int_0^\infty\frac{\sin ax}{x(x^4+b^4)}dx\\&&\quad+\int_{\G_R}\frac{e^{iaz}}{z(z^4+b^4)}dz+\int_{\G_\epsilon}\frac{e^{iaz}}{z(z^4+b^4)}dz\tag{1}\end{eqnarray}
この左辺は\begin{eqnarray}2\pi i\mathrm{Res}f(z)&&=2\pi i\displaystyle\lim_{z\to be^{\frac{\pi}{4}i}}(z-be^{\frac{\pi}{4}i})f(z)\\&&=2\pi i\displaystyle\lim_{z\to be^{\frac{\pi}{4}i}}\frac{e^{iaz}}{z(z+be^{\frac{\pi}{4}i})(z^2+ib^2)}\\&&=\frac{\pi}{2b^4i}e^{\frac{ab}{\sqrt{2}}(-1+i)}\\&&=\frac{\pi}{2b^4i}e^{-\frac{ab}{\sqrt{2}}}\left(\cos\frac{ab}{\sqrt{2}}+i\sin\frac{ab}{\sqrt{2}}\right)\\&&=\frac{\pi}{2b^4}e^{-\frac{ab}{\sqrt{2}}}\left(\sin\frac{ab}{\sqrt{2}}-i\cos\frac{ab}{\sqrt{2}}\right)\tag{2}\end{eqnarray}
(1)の右辺第3項を評価すると\begin{eqnarray}\left|\int_{\G_R}\frac{e^{iaz}}{z(z^4+b^4)}dz\right|&&\le\int_0^\frac{\pi}{2}\frac{e^{-aR\sin\t}}{R|R^4e^{4i\t}+b^4|}Rd\t\\&&\le\int_0^\frac{\pi}{2}\frac{d\t}{|R^4e^{4i\t}+b^4|}\\&&\le\int_0^\frac{\pi}{2}\frac{d\t}{|R^4-b^4|}\\&&=\frac{\pi}{2(R^4-b^4)}\\&&\xrightarrow[R\to\infty]{}0\tag{3}\end{eqnarray} また(1)の右辺第4項は\begin{eqnarray}\int_{\G_\epsilon}\frac{e^{iaz}}{z(z^4+b^4)}dz&&=\int_\frac{\pi}{2}^0\frac{e^{ia\epsilon e^{i\t}}}{\epsilon e^{i\t}(\epsilon^4 e^{4i\t}+b^4)}i\epsilon e^{i\t}d\t\\&&=-i\int^\frac{\pi}{2}_0\frac{e^{ia\epsilon e^{i\t}}}{\epsilon^4 e^{4i\t}+b^4}d\t\\&&=-i\int^\frac{\pi}{2}_0\frac{1}{b^4}d\t\\&&=-i\frac{\pi}{2b^4}\tag{4}\end{eqnarray}
(2)(3)(4)を(1)に用いて\begin{eqnarray}\frac{\pi}{2b^4}e^{-\frac{ab}{\sqrt{2}}}\left(\sin\frac{ab}{\sqrt{2}}-i\cos\frac{ab}{\sqrt{2}}\right)&&=\int_0^\infty\frac{\cos ax-e^{-ax}}{x(x^4+b^4)}dx\\&&\quad+i\int_0^\infty\frac{\sin ax}{x(x^4+b^4)}dx-i\frac{\pi}{2b^4}\end{eqnarray}両辺を実部・虚部に分けることにより
$$\int_0^\infty\frac{\cos ax-e^{-ax}}{x(x^4+b^4)}dx=\frac{\pi }{2b^4}e^{-\frac{ab}{\sqrt{2}}}\sin\frac{ab}{\sqrt{2}}$$$$\int_0^\infty\frac{\sin ax}{x(x^4+b^4)}dx=\frac{\pi}{2b^4}\left(1-e^{-\frac{ab}{\sqrt{2}}}\cos\frac{ab}{\sqrt{2}}\right)$$
類題はこちら:
Excercise of Contour Integral (Combination of Real and Imaginary Axis)
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。


