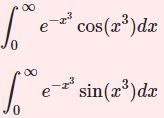$$I\equiv\int_{0}^\infty\ln(2-2\cos x^2)dx$$とその一般化$$I_p\equiv \int_{0}^\infty\ln(2-2\cos x^p)dx$$
$\cos^2x$ ではなくて $\cos(x^2)$ であることに注意してください。この積分は複素積分によって計算することができます。経路の取り方はフレネル積分のときと同じです。参考記事はこちら:
【複素解析】フレネル積分-三角関数の特殊な積分 sin x^2 , cos x^2
$\ln(1-e^{ix^2})$ なる関数を変形すると\begin{eqnarray}\ln(1-e^{ix^2})&&=\ln(1-\cos x^2-i\sin x^2)\\&&=\ln\left[(1-\cos x^2)^2+\sin^2x^2\right]^\frac{1}{2}e^{i\t}\quad(\t=\arg[1-e^{ix^2}])\\&&=\frac{1}{2}\ln(2-2\cos x^2)+i\t\end{eqnarray}実部が求める積分 $I$ の被積分関数となっています。したがって積分 $I$ は次のように書き換えることができます。
\begin{equation}I=2\mathfrak{R}\int_0^\infty\ln(1-e^{ix^2})dx\tag{1}\end{equation}
$\ln$ を級数展開します。$$\ln(1-e^{ix^2})=-\sum_{n=1}^\infty\frac{1}{n}\left(e^{ix^2}\right)^n$$これにより(1)は
\begin{equation}I=-2\sum_{n=1}^\infty\frac{1}{n}\mathfrak{R}\int_0^\infty e^{inx^2}dx\tag{2}\end{equation}
ここで複素積分 $\int e^{inz^2}dz$ 、その積分経路 $C$ を次の閉じた扇形にとります。半径は $R\to\infty$ です。
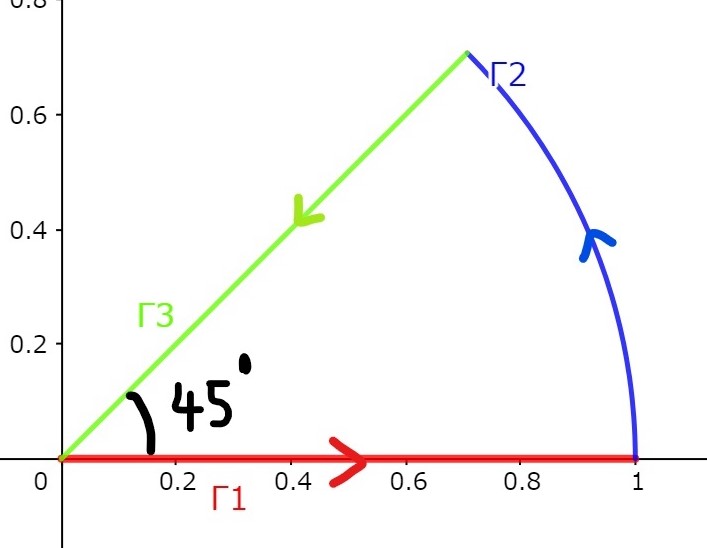
$C$ を上記のように3つに分けると、求めたい(1)は経路 $\G_1$ にあたります。すなわち$$\oint_Ce^{inz^2}dz=\int_0^\infty e^{inx^2}dx+\int_{\G_2}e^{inz^2}dz+\int_{\G_3}e^{inz^2}dz$$この被積分関数には極がありませんので周回積分はゼロです。したがって
\begin{equation}\int_0^\infty e^{inx^2}dx=-\int_{\G_2}e^{inz^2}dz-\int_{\G_3}e^{inz^2}dz\tag{3}\end{equation}
大きな円弧の積分値を評価しましょう。\begin{eqnarray}\left|\int_{\G_2}e^{inz^2}dz\right|&&=\left|\int_0^\frac{\pi}{4}e^{inR^2(\cos2\t+i\sin2\t)}iRe^{i\t}d\t\right|\\&&\le R\int_0^\frac{\pi}{4}\left|e^{-nR^2\sin2\t}\right|d\t\\&&\le R\int_0^\frac{\pi}{4}e^{-R^2\sin2\t}d\t\\&&=\frac{R}{2}\int_0^\frac{\pi}{2}e^{-R^2\sin\t}d\t\\&&\le\frac{R}{2}\int_0^\frac{\pi}{2}e^{-\frac{2R^2}{\pi}\t}d\t\\&&=-\frac{\pi}{4R}(e^{-R^2}-1)\\&&\xrightarrow[R\to\infty]{}0\tag{4}\end{eqnarray}
したがって円弧の積分はゼロに収束しますので、(3)は
\begin{equation}\int_0^\infty e^{inx^2}dx=-\int_{\G_3}e^{inz^2}dz\tag{5}\end{equation}
と簡略化できます。
$\G_3$ は偏角 $\pi/4$ の直線なので $z=e^{i\frac{\pi}{4}}x$ と置換すると\begin{eqnarray}\int_{\G_3}e^{inz^2}dz&&=\int_\infty^0 e^{-nx^2}e^{i\frac{\pi}{4}}dx\\&&=-\frac{1+i}{\sqrt{2}}\frac{1}{2}\sqrt{\frac{\pi}{n}}\end{eqnarray}(5)へ用いれば
\begin{equation}\int_0^\infty e^{inx^2}dx=\frac{1+i}{2\sqrt{2}}\sqrt{\frac{\pi}{n}}\tag{6}\end{equation}
求める積分 $I$ は(2)式で与えられるので\begin{eqnarray}I&&=-2\sum_{n=1}^\infty\frac{1}{n}\mathfrak{R}\int_0^\infty e^{inx^2}dx\\&&=-2\sum_{n=1}^\infty\frac{1}{n}\mathfrak{R}\frac{1+i}{2\sqrt{2}}\sqrt{\frac{\pi}{n}}\\&&=-\frac{\sqrt{\pi}}{\sqrt{2}}\sum_{n=1}^\infty\frac{1}{n\sqrt{n}}\end{eqnarray}以上より
$$\int_{0}^\infty\ln(2-2\cos x^2)dx=-\frac{\sqrt{\pi}}{\sqrt{2}}\zeta\left(\frac{3}{2}\right)$$
これで完成です。
$p$ を2以上の自然数として
$$I_p\equiv \int_{0}^\infty\ln(2-2\cos x^p)dx$$
を考えましょう。すると複素積分との関係は
\begin{equation}I_p=2\mathfrak{R}\int_0^\infty\ln(1-e^{ix^p})dx\tag{7}\end{equation}
級数展開すると
\begin{equation}I_p=-2\sum_{n=1}^\infty\frac{1}{n}\mathfrak{R}\int_0^\infty e^{inx^p}dx\tag{8}\end{equation}
ここで複素積分 $$\oint_C e^{inz^p}dz$$を考えます。 経路は先ほどと同様ですが、扇形の中心角を $\frac{\pi}{2p}$ とします。
周回積分はゼロ、円弧もまったく同様に計算すれば $0$ と評価されます。したがって
\begin{equation}\int_0^\infty e^{inx^p}dx=-\int_{\G_3}e^{inz^p}dz\tag{9}\end{equation}
$\G_3$ は偏角 $\pi/2p$ の直線なので $z=e^{i\frac{\pi}{2p}}x$ と置換すると\begin{eqnarray}-\int_{\G_3}e^{inz^p}dz&&=-\int_\infty^0 e^{-nx^p}e^{i\frac{\pi}{2p}}dx\\&&=e^{i\frac{\pi}{2p}}\int_0^\infty e^{-nx^p}dx\\&&=e^{i\frac{\pi}{2p}}n^{-1/p}\int_0^\infty e^{-x^p}dx\\&&=e^{i\frac{\pi}{2p}}\frac{n^{-1/p}}{p}\int_0^\infty y^{\frac{1}{p}-1}e^{-y}dy\\&&=e^{i\frac{\pi}{2p}}\frac{n^{-1/p}}{p}\G\left(\frac{1}{p}\right)\end{eqnarray}(9)へ適用して$$\int_0^\infty e^{inx^p}dx=e^{i\frac{\pi}{2p}}\frac{n^{-1/p}}{p}\G\left(\frac{1}{p}\right)$$(8)へ適用して\begin{eqnarray}I_p&&=-2\sum_{n=1}^\infty\frac{1}{n}\mathfrak{R}e^{i\frac{\pi}{2p}}\frac{n^{-1/p}}{p}\G\left(\frac{1}{p}\right)\\&&=-\frac{2}{p}\G\left(\frac{1}{p}\right)\cos\frac{\pi}{2p}\sum_{n=1}^\infty\frac{1}{n}n^{-1/p}\end{eqnarray}最終的に次の答えを得ます。
$$\int_{0}^\infty\ln(2-2\cos x^p)dx=-\frac{2}{p}\G\left(\frac{1}{p}\right)\zeta\left(1+\frac{1}{p}\right)\cos\frac{\pi}{2p}$$
フレネル積分に類似したその他の積分はこちら:
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。