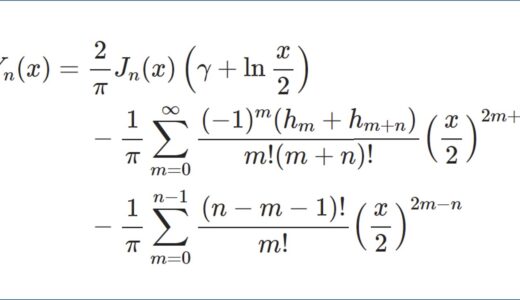Integrals and Miscellaneous 6

$$\sum_{n=1}^\infty\frac{H_n}{n}x^n=\frac{1}{2}\ln^2(1-x)+\mathrm{Li}_2(x)$$The Cauchy product of $-\log(1-x)$ and $\frac{1}{1-x}$ :$$\sum_{n=1}^\infty H_nx^n=-\frac{\log(1-x)}{1-x}$$Integrate from $0$ to $x$,\begin{eqnarray*}\frac{1}{2}\ln^2(1-x)&&=\sum_{n=1}^\infty\frac{H_n}{n+1}x^{n+1}\\&&=\frac{H_1}{2}x^2+\frac{H_2}{3}x^3+\cdots\\&&=\frac{1}{2}\left(H_2-\frac{1}{2}\right)x^2+\frac{1}{3}\left(H_3-\frac{1}{3}\right)+\cdots\\&&=\left(H_1x+\frac{H_2}{2}x^2+\frac{H_3}{3}x^3+\cdots\right)-\left(x+\frac{x^2}{2^2}+\frac{x^3}{3^2}\cdots\right)\\&&=\sum_{n=1}^\infty\frac{H_n}{n}x^n-\sum_{n=1}^\infty\frac{x^n}{n^2}\\&&=\sum_{n=1}^\infty\frac{H_n}{n}x^n-\mathrm{Li}_2(x)\end{eqnarray*}Hence,$$\sum_{n=1}^\infty\frac{H_n}{n}x^n=\frac{1}{2}\ln^2(1-x)+\mathrm{Li}_2(x)$$

$$\sum_{n=1}^\infty\frac{H_n}{2^nn^2}=\zeta(3)-\frac{\pi^2}{12}\ln2$$Define $f(x):=\displaystyle\sum_{n=1}^\infty\frac{H_n}{n^2}x^n$. We can see$$(xf'(x))'=\sum_{n=1}^\infty H_nx^{n-1}$$ it follows from $\sum_{n=1}^\infty H_nx^n=-\frac{\ln(1-x)}{1-x}$ that$$(xf'(x))'=-\frac{\ln(1-x)}{x}-\frac{\ln(1-x)}{1-x}$$Integrating from $0$ to $x$ we get$$f'(x)=\frac{\mathrm{Li}_2(x)}{x}+\frac{\ln^2(1-x)}{2x}$$Integrating again, we obtain$$f(x)=\mathrm{Li}_3(x)-\mathrm{Li}_3(1-x)+\mathrm{Li}_2(1-x)\ln(1-x)+\frac{1}{2}\ln x\ln^2(1-x)+\zeta(3)$$Substituting $x=1/2$ and applying $\mathrm{Li_2}(1/2)=\frac{\pi^2}{12}-\frac{\ln^22}{2}$, finally we have$$\sum_{n=1}^\infty\frac{H_n}{2^nn^2}=\zeta(3)-\frac{\pi^2}{12}\ln2$$

\begin{eqnarray*}\sum_{n=0}^\infty\frac{(2n)!!}{(2n+1)!!(2n+1)}&&=\sum_{n=0}^\infty\frac{1}{2n+1}\int_0^\frac{\pi}{2}\cos^{2n+1}xdx\\&&=\frac{1}{2}\int_0^\frac{\pi}{2}\ln\frac{1+\cos x}{1-\cos x}dx\\&&=-\int_0^\frac{\pi}{2}\ln\tan\frac{x}{2}dx\\&&=2\int_0^\frac{\pi}{2}\sum_{n=0}^\infty\frac{\cos(2n+1)x}{2n+1}dx\quad(*)\\&&=2\sum_{n=0}^\infty\frac{1}{2n+1}\left[\frac{\sin(2n+1)x}{2n+1}\right]_0^\frac{\pi}{2}\\&&=2\sum_{n=0}^\infty\frac{(-1)^n}{(2n+1)^2}\\&&=2\beta(2)\end{eqnarray*}Hence,$$\sum_{n=0}^\infty\frac{(2n)!!}{(2n+1)!!(2n+1)}=2G$$

(*) is proved here:

x^m/(sin x)^nの積分（logsinのフーリエ展開・ディリクレのベータ関数）

$$I(s):=\int_0^\frac{\pi}{2}\arctan(s\sin x)dx\quad ,\;I(0)=0$$\begin{eqnarray*}I'(s)&&=\int_0^\frac{\pi}{2}\frac{\sin x}{1+s^2-s^2\cos^2x}dx\\&&=\frac{1}{s\sqrt{1+s^2}}\ln(s+\sqrt{1+s^2})\quad(\mathrm{By\:substituting}\:\cos x=y)\end{eqnarray*}Integrating it to get $I(s)$,\begin{eqnarray*}I(s)&&=\int_0^s\frac{\ln(x+\sqrt{1+x^2})}{x\sqrt{1+x^2}}dx\\&&=\int_0^{\sinh^{-1}s}\frac{tdt}{\sinh t}\quad(x=\sinh t)\\&&=2\sum_{n=0}^\infty\int_0^{a}te^{-(2n+1)t}dt\quad(a\;\mathrm{denotes}\;\sinh^{-1}s)\\&&=2\sum_{n=0}^\infty\frac{1}{(2n+1)^2}-2a\sum_{n=0}^\infty\frac{(e^{-a})^{2n+1}}{2n+1}-2\sum_{n=0}^\infty\frac{(e^{-a})^{2n+1}}{(2n+1)^2}\\&&=\frac{\pi^2}{4}-a\ln\frac{1+e^{-a}}{1-e^{-a}}-2\left(\sum_{n=0}^\infty\frac{(e^{-a})^{n}}{n^2}-\sum_{n=0}^\infty\frac{(e^{-a})^{2n}}{(2n)^2}\right)\\&&=\frac{\pi^2}{4}-a\ln\frac{1+e^{-a}}{1-e^{-a}}-2\mathrm{Li}_2(e^{-a})+\frac{1}{2}\mathrm{Li}_2(e^{-2a})\\&&=\frac{\pi^2}{4}-a\ln\frac{1+e^{-a}}{1-e^{-a}}-\mathrm{Li}_2(e^{-a})+\mathrm{Li}_2(-e^{-a})\end{eqnarray*}When $s=1$, letting $a=\ln(\sqrt{2}+1)$ we get $I(1)$ , namely,$$\int_0^\frac{\pi}{2}\arctan(\sin x)dx=\frac{\pi^2}{8}-\frac{1}{2}\ln^2(\sqrt{2}-1)$$When $s=2$, using the identity $\mathrm{Li}_2(\phi^{-3})-\mathrm{Li}_2(-\phi^{-3})=\frac{\pi^2}{12}-\frac{3}{2}\ln^2\phi$ ,$$\int_0^\frac{\pi}{2}\arctan(2\sin x)dx=\frac{\pi^2}{6}-\frac{3}{2}\ln^2\phi$$

Detailed proof:

2022年6月6日 arctan(μsin x)とarctan(μcsc x)の積分（二重対数関数と黄金比）

$$I:=\int_0^1\frac{\ln t\ln^2(1-t)}{t}dt$$

The beta function:$$B(x,y)=\int_0^1 t^{x-1}(1-t)^{y-1}dt$$Differentiate twice w.r.t $y$ then once w.r.t $x$.$$\frac{\partial^3B(x,y)}{\partial x\partial^2y}=\int_0^1 t^{x-1}(1-t)^{y-1}\ln t\ln^2(1-t)dt$$Therefore,$$I=\left.\frac{\partial^3B(x,y)}{\partial x\partial^2y}\right|_{x=+0,y=1}$$Differentiate the relationship between the beta and the gamma function,\begin{eqnarray*}\left.\frac{\partial^3B(x,y)}{\partial x\partial^2y}\right|_{y=1}=&&\frac{1}{x}\left[\frac{\psi'(x+1)-\psi'(1)}{x}-\psi''(x+1)\right]\\&&-\left(\frac{\psi(x+1)-\psi(1)}{x}\right)^2+2\psi'(x+1)\frac{\psi(x+1)-\psi(1)}{x}\end{eqnarray*}\begin{eqnarray*}&&\psi(x+1)=\psi(1)+\zeta(2)x+O(x^2)\\&&\psi'(x+1)=\zeta(2)-2\zeta(3)x+3\zeta(4)x^2+O(x^3)\\&&\psi''(x+1)=-2\zeta(3)+6\zeta(4)x+O(x^2)\end{eqnarray*}Using them, we obtain the limit as $x$ goes to $+0$ and hence$$I=-\frac{\pi^4}{180}$$

$$I=\int_0^1\frac{\ln^2t\ln(1-t)}{t}dt$$

Integration by parts in the polylog gives:\begin{eqnarray*}\Li_4(x)&&=\int_0^x\frac{\Li_3(t)}{t}dt\\&&=\ln x\Li_3(x)-\int_0^x\frac{\ln t\Li_2(t)}{t}dt\\&&=\ln x\Li_3(x)-\frac{1}{2}\ln^2x\Li_2(x)-\frac{1}{2}\int_0^x\frac{\ln^2t\ln(1-t)}{t}dt\end{eqnarray*}Substituting $x=1$, we get$$\int_0^1\frac{\ln^2t\ln(1-t)}{t}dt=-2\Li_4(1)=-2\zeta(4)$$Hence,$$\int_0^1\frac{\ln^2t\ln(1-t)}{t}dt=-\frac{\pi^4}{45}$$

\begin{eqnarray}\int_0^x&&\frac{\ln^2t\ln(1-t)}{1-t}dt\\&&=-2\left[\Li_4\left(\frac{-x}{1-x}\right)+\Li_4(x)-\Li_4(1-x)+\zeta(4)\right]\\&&\quad+2\Bigl[\ln(1-x)\Li_3(x)-\ln x\Li_3(1-x)\Bigr]\\&&\quad+2\ln x\ln(1-x)\Li_2(1-x)-\frac{\pi^2}{6}\ln^2(1-x)\\&&\quad+\frac{\ln^2(1-x)}{12}\Bigl[6\ln^2x+4\ln x\ln(1-x)-\ln^2(1-x)\Bigr]\\&&\quad+2\zeta(3)\ln\frac{x}{1-x}\end{eqnarray}

proof here:

2022年6月17日 4次の多重対数関数を応用する積分

$$I:=\int_0^\frac{1}{2}\frac{\ln^2t\ln(1-t)}{1-t}dt$$

Using the formula which we obtained before:\begin{eqnarray}\int_0^x&&\frac{\ln^2t\ln(1-t)}{1-t}dt\\&&=-2\left[\Li_4\left(\frac{-x}{1-x}\right)+\Li_4(x)-\Li_4(1-x)+\zeta(4)\right]\\&&\quad+2\Bigl[\ln(1-x)\Li_3(x)-\ln x\Li_3(1-x)\Bigr]\\&&\quad+2\ln x\ln(1-x)\Li_2(1-x)-\frac{\pi^2}{6}\ln^2(1-x)\\&&\quad+\frac{\ln^2(1-x)}{12}\Bigl[6\ln^2x+4\ln x\ln(1-x)-\ln^2(1-x)\Bigr]\\&&\quad+2\zeta(3)\ln\frac{x}{1-x}\end{eqnarray}Substituting $x=1/2$, we get$$\int_0^\frac{1}{2}\frac{\ln^2t\ln(1-t)}{1-t}dt=-\frac{\pi^4}{360}-\frac{\ln^42}{4}$$

The proof of the formula is here:

4次の多重対数関数を応用する積分

$$I:=\int_0^\frac{1}{2}\frac{\ln^2(1-t)}{t}dt$$

Integrating in $\Li_3(x)$ by parts gives\begin{eqnarray*}\Li_3(x)&&=\int_0^x\frac{\Li_2(t)}{t}dt\\&&=\ln x\Li_2(x)+\frac{1}{2}\ln^2x\ln(1-x)+\frac{1}{2}\int_0^x\frac{\ln^2t}{1-t}dt\end{eqnarray*}Replacing $x$ with $1-x$,we get\begin{eqnarray*}\Li_3(1-x)&&=\ln (1-x)\Li_2(1-x)+\frac{1}{2}\ln x\ln^2(1-x)-\frac{1}{2}\int_1^{x}\frac{\ln^2(1-t)}{t}dt\\&&=\ln (1-x)\Li_2(1-x)+\frac{1}{2}\ln x\ln^2(1-x)\\&&\quad+\frac{1}{2}\int_0^1\frac{\ln^2(1-t)}{t}dt-\frac{1}{2}\int_0^{x}\frac{\ln^2(1-t)}{t}dt\end{eqnarray*}We find $\zeta(3)$ equals to the third term by letting $x=0$ and hence,\begin{eqnarray*}\int_0^x\frac{\ln^2(1-t)}{t}dt&&=-2\Li_3(1-x)+2\ln (1-x)\Li_2(1-x)\\&&\quad+\ln x\ln^2(1-x)+2\zeta(3)\end{eqnarray*}Substituting $x=1/2$, we finally have$$\int_0^\frac{1}{2}\frac{\ln^2(1-t)}{t}dt=\frac{1}{4}\zeta(3)-\frac{1}{3}\ln^32$$

$$I(x):=\int_0^x\frac{\ln^2(1+t)}{t}dt$$Integrating the defining equation of $\Li_3(x)$ by parts gives\begin{eqnarray*}\Li_3(x)&&=\int_0^x\frac{\Li_2(t)}{t}dt\\&&=\ln x\Li_2(x)+\frac{1}{2}\ln^2x\ln(1-x)+\frac{1}{2}\int_0^x\frac{\ln^2t}{1-t}dt\end{eqnarray*}Setting $x=1$, we find $\displaystyle\int_0^1\frac{\ln^2t}{1-t}dt=2\zeta(3)$ . Then replacing $x$ with $1/(1+x)$ above, we get\begin{eqnarray}\Li_3\left(\frac{1}{1+x}\right)&&=-\ln(1+x)\Li_2\left(\frac{1}{1+x}\right)\\&&\quad+\frac{1}{2}\ln^2(1+x)\ln\frac{x}{1+x}+\frac{1}{2}\int_0^\frac{1}{1+x}\frac{\ln^2t}{1-t}dt\tag{1}\end{eqnarray}The integral in the right-hand side is\begin{eqnarray} \int_0^\frac{1}{1+x}\frac{\ln^2t}{1-t}dt&&=\int_0^1\frac{\ln^2t}{1-t}dt+\int_1^\frac{1}{1+x}\frac{\ln^2t}{1-t}dt\\&&=2\zeta(3)-\int_0^x\frac{\ln^2(1+u)}{u(1+u)}du\quad(t=\frac{1}{1+u})\\&&=2\zeta(3)+\frac{1}{3}\ln^3(1+x)-\int_0^x\frac{\ln^2(1+u)}{u}du\tag{2}\end{eqnarray}From (1),(2) we obtain\begin{eqnarray*}\int_0^x\frac{\ln^2(1+t)}{t}dt&&=-2\Li_3\left(\frac{1}{1+x}\right)-2\ln(1+x)\Li_2\left(\frac{1}{1+x}\right)\\&&\quad+\ln x\ln^2(1+x)-\frac{2}{3}\ln^3(1+x)+2\zeta(3)\end{eqnarray*}

$$I:=\int_0^1\frac{\arctan x}{1+x}dx$$Letting $x=\frac{1-t}{1+t}$, we obtain$$I=\int_0^1\frac{\arctan\frac{1-t}{1+t}}{1+t}dt$$Therefore,\begin{eqnarray*}2I&&=\int_0^1\frac{\arctan x+\arctan\frac{1-x}{1+x}}{1+x}dx\\&&=\frac{\pi}{4}\int_0^1\frac{dx}{1+x}\\&&=\frac{\pi}{4}\ln2\end{eqnarray*}Hence,$$\int_0^1\frac{\arctan x}{1+x}dx=\frac{\pi}{8}\ln2$$

Another solution:$$\int_0^1\frac{\arctan x}{1+x}dx\overset{IBP}{=}\frac{\pi}{4}\ln2-\int_0^1\frac{\ln (1+x)}{1+x^2}dx$$$$\int_0^1\frac{\ln (1+x)}{1+x^2}dx=\int_0^1\frac{\ln 2-\ln(1+t)}{1+t^2}dt\quad(x=\frac{1-t}{1+t})$$Hence we get$$\int_0^1\frac{\ln (1+x)}{1+x^2}dx=\frac{\ln2}{2}\int_0^1\frac{1}{1+x^2}dx=\frac{\pi\ln2}{8}$$Therefore,$$\int_0^1\frac{\arctan x}{1+x}dx=\frac{\pi}{4}\ln2-\frac{\pi}{8}\ln2=\frac{\pi}{8}\ln2$$

$$I(x):=\int_0^x\frac{\ln^3(1+u)}{u}du$$Integrating the defining equation of $\Li_4(x)$ by parts gives\begin{eqnarray}\Li_4(x)&&=\ln x\Li_3(x)-\frac{1}{2}\ln^2x\Li_2(x)-\frac{1}{6}\ln^3x\ln(1-x)-\frac{1}{6}\int_0^x\frac{\ln^3t}{1-t}dt\tag{1}\end{eqnarray}Substitution $x=1$ gives\begin{equation}\int_0^1\frac{\ln^3t}{1-t}dt=-6\Li_4(1)=-\frac{\pi^4}{15}\tag{2}\end{equation}and we substitute $x\to\frac{1}{1+x}$ and rewrite the remaining integral in (1) as\begin{eqnarray}\int_0^\frac{1}{1+x}\frac{\ln^3t}{1-t}dt &=& \int_0^1\frac{\ln^3t}{1-t}dt+\int_1^\frac{1}{1+x}\frac{\ln^3t}{1-t}dt\\&=&-\frac{\pi^4}{15}+\int_1^\frac{1}{1+x}\frac{\ln^3t}{1-t}dt\quad(\because(2))\\&=&-\frac{\pi^4}{15}+\int_0^x\frac{\ln^3(1+u)}{u(1+u)}du\quad(t=\frac{1}{1+u})\\&=&-\frac{\pi^4}{15}+\int_0^x\frac{\ln^3(1+u)}{u}du-\int_0^x\frac{\ln^3(1+u)}{1+u}du\\&=&-\frac{\pi^4}{15}+\int_0^x\frac{\ln^3(1+u)}{u}du-\frac{1}{4}\ln^4(1+x)\tag{3}\end{eqnarray}From (1)(3) we have\begin{eqnarray*}\int_0^x\frac{\ln^3(1+u)}{u}du&=& -6\Li_4\left(\frac{1}{1+x}\right)-6\ln(1+x)\Li_3\left(\frac{1}{1+x}\right)\\&&-3\ln^2(1+x)\Li_2\left(\frac{1}{1+x}\right)+\ln x\ln^3(1+x)-\frac{3}{4}\ln^4(1+x)+\frac{\pi^4}{15}\end{eqnarray*}Especially, $x=1$ yields\begin{eqnarray*}\int_0^1\frac{\ln^3(1+u)}{u}du&=& -6\Li_4\left(\frac{1}{2}\right)-\frac{21\ln2}{4}\zeta(3)+\frac{\pi^2}{4}\ln^22-\frac{\ln^42}{4}+\frac{\pi^4}{15}\end{eqnarray*}

$$\int_0^\infty\frac{\cos ax-e^{-ax}}{x(x^4+b^4)}dx=\frac{\pi }{2b^4}e^{-\frac{ab}{\sqrt{2}}}\sin\frac{ab}{\sqrt{2}}$$$$\int_0^\infty\frac{\sin ax}{x(x^4+b^4)}dx=\frac{\pi}{2b^4}\left(1-e^{-\frac{ab}{\sqrt{2}}}\cos\frac{ab}{\sqrt{2}}\right)$$Proof here:

2022年6月19日 複素積分演習 cosx と e^-xの混合（4分円の周回積分）

$$I:=\int_0^1\frac{\ln x\ln^3(1-x)}{x}dx$$\begin{eqnarray*}I&&=-\int_0^1\frac{\ln^3 x\ln(1-x)}{1-x}dt\quad(x\to 1-x)\\&&=\int_0^1\ln^3x\sum_{n=1}^\infty H_nx^ndx\quad(H_n \mathrm{\:denotes \:the \:harmonic \:number})\\&&=\sum_{n=1}^\infty H_n\int_0^1x^n\ln^3 xdx\\&&=6\sum_{n=1}^\infty\frac{H_n}{(n+1)^4}=6\sum_{n=1}^\infty\frac{H_{n-1}}{n^4}\\&&=6\sum_{n=1}^\infty\frac{H_n-\frac{1}{n}}{n^4}\\&&=6\sum_{n=1}^\infty\frac{H_n}{n^4}-6\zeta(5)\end{eqnarray*}We obtained here that$$\sum_{n=1}^\infty\frac{H_n}{n^4}=3\zeta(5)-\zeta(2)\zeta(3)$$Hence,$$\int_0^1\frac{\ln x\ln^3(1-x)}{x}dx=12\zeta(5)-\pi^2\zeta(3)$$

$$I:=\int_0^\frac{\pi}{2}\t^2\ln^2 (2\cos\t) d\t$$We obtained the identity of the reciprocal beta function:$$I(x,y):=\int_0^\frac{\pi}{2}(2\cos\t)^{x-1}\cos y\t d\t=\frac{\pi}{2xB(\frac{x+y+1}{2},\frac{x-y+1}{2})}$$Now we can see $$I=-\left.\frac{\partial^4I(x,y)}{\partial x^2\partial y^2}\right|_{x=1,y=0}$$Differentiating $I(x,y)$ twice w.r.t $y$, substituting $y=0$, we get$$\left.\frac{\partial^2I(x,y)}{\partial y^2}\right|_{y=0}=-\frac{\pi}{4}\frac{\G(x)\psi'(\frac{x+1}{2})}{\G^2(\frac{x+1}{2})}$$Then differentiating twice w.r.t $x$ and letting $x=1$,we have\begin{eqnarray*}\left.\frac{\partial^4I(x,y)}{\partial x^2\partial y^2}\right|_{x=1,y=0}&&=-\frac{\pi}{4}\left(\frac{1}{2}\psi'(1)^2+\frac{1}{4}\psi'''(1)\right)\\&&=-\frac{\pi}{4}\left(\frac{1}{2}\zeta(2)^2+\frac{6}{4}\zeta(4)\right)\\&&=-\frac{11}{1440}\pi^5\end{eqnarray*}Hence,$$\int_0^\frac{\pi}{2}\t^2\ln^2 (2\cos\t) d\t=\frac{11}{1440}\pi^5$$

Proof of the identity:

2022年5月6日 ベータ関数の逆数の積分表示（複素積分演習）