前回の記事：
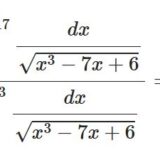ペー関数を使って楕円積分を変換する具体例
これと全く同じ方法で新しい等式をつくります。
\begin{align}\cfrac{\displaystyle\int_1^{49}\frac{dx}{\sqrt{x^3-x}}}{\displaystyle\int_1^2\frac{dx}{\sqrt{x^3-x}}} &=2\tag{1}\\[1em]\cfrac{\displaystyle\int_1^{\frac{289}{49}}\frac{dx}{\sqrt{x^3-x}}}{\displaystyle\int_1^\frac{3}{2}\frac{dx}{\sqrt{x^3-x}}} &=2\tag{2}\\[1em]\cfrac{\displaystyle\int_1^{\frac{529}{49}}\frac{dx}{\sqrt{x^3-x}}}{\displaystyle\int_1^\frac{5}{3}\frac{dx}{\sqrt{x^3-x}}} &=2\tag{3}\\[1em]\end{align}
\begin{align}\cfrac{\displaystyle\int_1^{19}\frac{dx}{\sqrt{16x^3-21x+5}}}{\displaystyle\int_1^{\frac{7}{4}}\frac{dx}{\sqrt{16x^3-21x+5}}}\tag{4}\\[1em]\cfrac{\displaystyle\int_1^{499/121}\frac{dx}{\sqrt{16x^3-21x+5}}}{\displaystyle\int_1^{11/8}\frac{dx}{\sqrt{16x^3-21x+5}}}\tag{5}\\[1em]\cfrac{\displaystyle\int_1^{271}\frac{dx}{\sqrt{16x^3-21x+5}}}{\displaystyle\int_1^{17/8}\frac{dx}{\sqrt{16x^3-21x+5}}}\tag{6}\\[1em]\cfrac{\displaystyle\int_1^{9949/121}\frac{dx}{\sqrt{16x^3-21x+5}}}{\displaystyle\int_1^{2}\frac{dx}{\sqrt{16x^3-21x+5}}}\tag{7}\end{align}
$$I:=\int_{e_1}^a\frac{dx}{\sqrt{4x^3-g_2x-g_3}}$$$$J:=\int_{e_1}^b\frac{dx}{\sqrt{4x^3-g_2x-g_3}}$$とおきます。$e_1<a<b$ なる条件を課します。$$\wp(2I)=\wp(J)$$なる方程式を立てて $2I=J$ となる条件を見つけます。
まず前半３つの式について。$e_1=1$ , $e_2=0$ , $e_3=-1$ のとき、$g_2=4$ , $g_3=0$ であり、\begin{equation}b=\left(\frac{a^2+2a-1}{a^2-2a-1}\right)^2\tag{8}\end{equation}を満たす $a,b$ を適当に探します。
後半の式について。$e_1=1$, $e_2=\frac{1}{4}$ のとき、$g_2=\frac{21}{4}$ , $g_3=-\frac{5}{4}$ であり、\begin{equation}b=\frac{256a^4+704a^3+672a^2-1564a+661}{(16a^2-32a-11)^2}\tag{9}\end{equation}を満たす $a,b$ を適当に探します。
もっと奇麗な組が見つかるといいんですけどね。
Please support me!
記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。
