$\mu>0$ , $-\frac{\pi}{2}\le x\le\frac{\pi}{2}$ とすると\begin{eqnarray}\cos^\mu x=&&\frac{\G(\mu+1)}{2^{\mu-1}\G(\frac{\mu}{2}+1)^2}\\&&\cdot\left[\frac{1}{2}+\frac{\mu}{\mu+2}\cos2x+\frac{\mu(\mu-2)}{(\mu+2)(\mu+4)}\cos4x+\cdots\right]\tag{1}\end{eqnarray}
$\cos^\mu$ のフーリエ展開の式ですが、$\mu$ が整数とは限らないところがポイントです。これを導出しましょう！
$-L\le x\le L$ の範囲における $f(x)$ のフーリエ展開は$$f(x)=\frac{a_0}{2}+\sum_{n=1}^\infty\left[a_n\cos\left(\frac{n\pi x}{L}\right)+b_n\sin\left(\frac{n\pi x}{L}\right)\right]$$
いま $f(x)=\cos^\mu x$ とすると、偶関数なので $b_n=0$ です。また $L=\frac{\pi}{2}$ とすれば $-\frac{\pi}{2}\le x\le\frac{\pi}{2}$ において$$\cos^\mu x=\frac{a_0}{2}+\sum_{n=1}^\infty a_n\cos2n x$$ここで各項の係数は$$a_n=\frac{2}{\pi}\int_{-\frac{\pi}{2}}^\frac{\pi}{2}\cos^\mu \t\cos 2n\t d\t$$で求まります。被積分関数は偶関数なので
\begin{equation}a_n=\frac{4}{\pi}\int_0^\frac{\pi}{2}\cos^\mu \t\cos 2n\t d\t\tag{2}\end{equation}
(2)は次の公式から計算することができます。
$s>0$ のとき\begin{equation}\int_0^\frac{\pi}{2}\cos^{s-1}\t\cos a\t d\t=\frac{\pi}{2^{s}sB(\frac{s+a+1}{2},\frac{s-a+1}{2})}\tag{3}\end{equation}
これの導出については：
実際、Whittaker-Watsonではこのベータ関数に関する等式を示す演習をさせた後で本ページのテーマを問うています。
古いですが有名な書物で、どんどん改訂版が出ています。前半は解析学一般、後半は特殊関数という内容で、網羅的に勉強できます。演習問題に解答がないのが昔ながらのものって感じ。2022/11/6現在、最新版は5th Editionで私も所有していますが、廉価な3rdとかでも十分かと。
A Course of Modern Analysis: fifth Edition
A Course of Modern Analysis: Third Edition
ここで $s-1=\mu$ , $a=2n$ とおけば$$\int_0^\frac{\pi}{2}\cos^\mu\t\cos 2n\t d\t=\frac{\pi}{2^{\mu+1}(\mu+1)B(\frac{\mu}{2}+n+1,\frac{\mu}{2}-n+1)}$$(2)より
\begin{equation}a_n=\frac{1}{2^{\mu-1}(\mu+1)B(\frac{\mu}{2}+n+1,\frac{\mu}{2}-n+1)}\tag{4}\end{equation}
これで展開の係数 $a_n$ が分かりました。あとは整えるだけです。
$B(x,y)=\frac{\G(x)\G(y)}{\G(x+y)}$ を用いて(4)をガンマ関数に書き直します。\begin{eqnarray}a_n&&=\frac{\G(\mu+2)}{2^{\mu-1}(\mu+1)\G(\frac{\mu}{2}+n+1)\G(\frac{\mu}{2}-n+1)}\\&&=\frac{\G(\mu+1)}{2^{\mu-1}\G(\frac{\mu}{2}+n+1)\G(\frac{\mu}{2}-n+1)}\tag{5}\end{eqnarray}$n=0$ とすると
\begin{equation}\frac{a_0}{2}=\frac{1}{2}\frac{\G(\mu+1)}{2^{\mu-1}\G(\frac{\mu}{2}+1)^2}\tag{6}\end{equation}
$n\ge 1$ に対しては$$\G\left(\frac{\mu}{2}+n+1\right)=\left(\frac{\mu}{2}+n\right)\left(\frac{\mu}{2}+n-1\right)\cdots\left(\frac{\mu}{2}+1\right)\cdot\G\left(\frac{\mu}{2}+1\right)$$$$\G\left(\frac{\mu}{2}-n+1\right)=\frac{\G(\frac{\mu}{2}+1)}{(\frac{\mu}{2}-n+1)(\frac{\mu}{2}-n+2)\cdots(\frac{\mu}{2})}$$を(5)に用いて\begin{eqnarray*}a_n&&=\frac{\G(\mu+1)}{2^{\mu-1}}\frac{(\frac{\mu}{2}-n+1)(\frac{\mu}{2}-n+2)\cdots(\frac{\mu}{2})}{\left(\frac{\mu}{2}+n\right)\left(\frac{\mu}{2}+n-1\right)\cdots\left(\frac{\mu}{2}+1\right)\cdot\G\left(\frac{\mu}{2}+1\right)^2}\\&&=\frac{\G(\mu+1)}{2^{\mu-1}\G(\frac{\mu}{2}+1)^2}\frac{\mu(\mu-2)\cdots(\mu-2n+2)}{(\mu+2)(\mu+4)\cdots(\mu+2n)}\end{eqnarray*}
以上より
$n\ge 1$ で\begin{equation}a_n=\frac{\G(\mu+1)}{2^{\mu-1}\G(\frac{\mu}{2}+1)^2}\frac{\mu(\mu-2)\cdots(\mu-2n+2)}{(\mu+2)(\mu+4)\cdots(\mu+2n)}\tag{7}\end{equation}
展開の係数(6)(7)より結局
$\mu>0$ , $-\frac{\pi}{2}\le x\le\frac{\pi}{2}$ とすると\begin{eqnarray}\cos^\mu x=&&\frac{\G(\mu+1)}{2^{\mu-1}\G(\frac{\mu}{2}+1)^2}\\&&\cdot\left[\frac{1}{2}+\frac{\mu}{\mu+2}\cos2x+\frac{\mu(\mu-2)}{(\mu+2)(\mu+4)}\cos4x\cdots\right]\tag{8}\end{eqnarray}
せっかくなのでいくつか代入して確かめましょう。
$\mu=2$ とすると右辺の級数は $\mu-2$ が現れる項で打ち切りとなります。$$\cos^2x=\frac{1}{2}(1+\cos2x)$$$\mu=4$ とすると $\mu-4$ が現れる項で打ち切りとなります。$$\cos^4x=\frac{3}{8}+\frac{1}{2}\cos2x+\frac{1}{8}\cos 4x$$このように $\mu$ が偶数であれば有限和となることが分かります。
一方 $\mu$ が奇数のときは打ち切られず無限級数です。$\mu=1$ なら$$\cos x=\frac{4}{\pi}\left(\frac{1}{2}+\frac{1}{3}\cos2x-\frac{1}{15}\cos4x+\frac{1}{35}\cos6x-\cdots\right)$$と続いていきます。
この公式は $\mu$ が非整数でも大丈夫なので、$\mu=1/2$ としてみると$$\sqrt{\cos x}=\frac{4\sqrt{2}}{\pi^{\frac{3}{2}}}\G\left(\frac{3}{4}\right)^2\left[\frac{1}{2}+\frac{1}{5}\cos2x-\frac{1}{15}\cos4x+\frac{7}{195}\cos6x-\cdots\right]$$計算が合っていればこうなります。
$\cos 2nx$ の級数で表せることで次のような問題を考えることができます。
$$\int_0^\frac{\pi}{2}\sqrt{\cos x}dx=\sqrt{\frac{2}{\pi}}\G\left(\frac{3}{4}\right)^2$$
この積分はベータ関数を直接使うなどの方法がありますが、先ほどの$$\sqrt{\cos x}=\frac{4\sqrt{2}}{\pi^{\frac{3}{2}}}\G\left(\frac{3}{4}\right)^2\left[\frac{1}{2}+\frac{1}{5}\cos2x-\frac{1}{15}\cos4x+\frac{7}{195}\cos6x-\cdots\right]$$を使いましょう。項別積分すると $\sin 2nx$ が現れ、$n=0$ のみの項が残されます。$$\int_0^\frac{\pi}{2}\sqrt{\cos x}dx=\frac{4\sqrt{2}}{\pi^{\frac{3}{2}}}\G\left(\frac{3}{4}\right)^2\cdot\frac{\pi}{4}$$よって上式を得ます。
はるか以前に書いた記事：
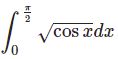$\int\sqrt{\cos x}dx$とガンマ関数・ベータ関数 $$\int_0^\frac{\pi}{4}\sqrt{\cos x}dx\approx\sqrt{\frac{2}{\pi}}\G\left(\frac{3}{4}\right)^2\left(\frac{1}{2}+\frac{44}{117\pi}\right)$$
先ほどと積分範囲が違います。今回は$n=0,1,3,5\cdots$ の項が残りますが、途中までで止めます。$$\int_0^\frac{\pi}{4}\sqrt{\cos x}dx\approx\frac{4\sqrt{2}}{\pi^{\frac{3}{2}}}\G\left(\frac{3}{4}\right)^2\left[\frac{x}{2}+\frac{\sin2x}{10}+\frac{7}{1170}\sin6x\right]_0^\frac{\pi}{4}$$これを整理すると上式を得ます。別に大した近似式ではありませんね・・・。
ベータ関数を基本から見たい場合は：
その他、ベータ関数の記事は：
$\int\sqrt[n]{\tan x}dx$ とベータ関数
Please support me!
記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。
