Integrals and Miscellaneous 20

$f(z):=(1-z^3)^{-1/2}$ , $C$ is the contour which consists of two lines and two arcs. One of the lines is indented at $z=1$ by an arc of radius $1/R$. The radius of the other arc is $R$.

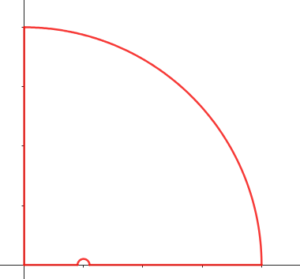
From the Cauthy's theorem we find $\oint_C f(z)dz=0$. The integral round the arcs tend to zero.\begin{eqnarray*}\oint f(z)dz &=&\int_0^1(1-x^3)^{-\frac{1}{2}}dx+\int_1^\infty\left\{(x-1)e^{-\pi i}\right\}^{-\frac{1}{2}}(1+x+x^2)^{-\frac{1}{2}}dx+i\int_\infty^0(1+ix^3)^{-\frac{1}{2}}dx\\&=&\int_0^1(1-x^3)^{-\frac{1}{2}}dx+i\int_1^\infty(x^3-1)^{-\frac{1}{2}}dx\\&&\quad-i\int_0^\infty(1+ix^3)^{-\frac{1}{2}}dx\\&=&\int_0^1(1-x^3)^{-\frac{1}{2}}dx+i\int_1^\infty(x^3-1)^{-\frac{1}{2}}dx\\&&\quad-ie^{-\frac{\pi}{6}i}\int_0^\infty(1+y^3)^{-\frac{1}{2}}dx\end{eqnarray*}Hence,\begin{eqnarray*}\int_0^1(1-x^3)^{-\frac{1}{2}}dx&=&\frac{1}{2}\int_0^\infty(1+x^3)^{-\frac{1}{2}}dx=\frac{1}{2}\int_{-\infty}^0(1-x^3)^{-\frac{1}{2}}dx\\\int_1^\infty(x^3-1)^{-\frac{1}{2}}dx&=&\frac{\sqrt{3}}{2}\int_0^\infty(1+x^3)^{-\frac{1}{2}}dx\end{eqnarray*}Therefore,\begin{eqnarray*}\int_{-\infty}^1(1-x^3)^{-\frac{1}{2}}dx&=&\frac{3}{2}\int_0^\infty(1+x^3)^{-\frac{1}{2}}dx\\\int_1^\infty(x^3-1)^{-\frac{1}{2}}dx&=&\frac{\sqrt{3}}{2}\int_0^\infty(1+x^3)^{-\frac{1}{2}}dx\end{eqnarray*}$$\therefore\quad\int_{-\infty}^1(1-x^3)^{-\frac{1}{2}}dx=\sqrt{3}\int_1^\infty(x^3-1)^{-\frac{1}{2}}dx$$

$$\int_0^1\int_0^1\frac{dxdy}{1+ixy}=G-i\frac{\pi^2}{48}$$PROOF:
Substituting $y=u/x$ gives\begin{align}LHS &= \int_0^1\frac{dx}{x}\int_0^x\frac{du}{1+iu} \\&=\int_0^1\frac{\arctan x}{x}dx-\frac{i}{2}\int_0^1\frac{\ln(1+x^2)}{x}dx\end{align}We obtained $$\int_0^1\frac{\arctan x}{x}dx=G$$ in "2022/4/3" and \begin{align} \int_0^1\frac{\ln(1+x^2)}{x}dx &=-\sum_{n=1}^\infty\frac{(-1)^n}{n}\int_0^1 x^{2n-1}dx\\&=-\frac{1}{2}\sum_{n=1}^\infty\frac{(-1)^n}{n^2}\\&=\frac{1}{4}\zeta(2)\end{align}

※そもそも最初から級数にすればよかった。$$\int_0^1\int_0^1\frac{dxdy}{1+ixy}=\sum_{n=1}^\infty\int_0^1\int_0^1(-ixy)^{n-1}dxdy$$

$$\int_0^1\int_0^1\frac{(-\ln xy)^a}{1-xy}(1-x)dxdy=\G(a+2)\left\{\zeta(a+2)-\frac{1}{a+1}\right\}$$PROOF.
Substituting $y=u/x$ yields\begin{align} LHS &= \int_0^1dx\int_0^xdu \frac{(-\ln u)^a}{1-u}\frac{1-x}{x} \\&= \int_0^1du\int_u^1dx\frac{(-\ln u)^a}{1-u}\frac{1-x}{x}\\ &= \int_0^1\frac{(-\ln u)^a}{1-u}(-\ln u+u-1)du \\&=\int_0^\infty \left(\frac{t^{a+1}}{e^t-1}-t^ze^{-t}\right)dt\quad(u=e^{-t})\\ &= \G(a+2)\left\{\zeta(a+2)-\frac{1}{a+1}\right\}\end{align}where we used$$\zeta(s)=\frac{1}{\G(s)}\int_0^\infty\frac{x^{s-1}}{e^{x}-1}dx$$ obtained here.

$a\to -1$ yields $$\int_0^1\int_0^1\frac{1}{(1-xy)\ln xy}(1-x)dxdy=-\g$$ from$$\displaystyle\lim_{s\to 1}\left(\zeta(s,a)-\frac{1}{s-1}\right)=-\psi(a)$$ we found here.

REFERENCE:
Chapman, R., A proof of Hadjicostas's conjecture.(2004)

$\Phi(z,s,a)$ denotes Lerch transcendent.$$\dd{\Phi}{s}(-1,-1,1)=\ln\frac{A^3}{2^{1/3}e^{1/4}}$$PROOF.
\begin{align}LHS &= \left.\frac{d}{ds}\left(1-\frac{1}{2^{s-1}}\right)\zeta(s)\right|_{s=-1}\\&= -3\zeta'(-1)+4\zeta(-1)\ln 2\\&=-\frac{\ln 2}{3}-\frac{1}{4}+3\ln A\end{align}

REFERENCE:
Guillera, J., Sondow, J. Double integrals and infinite products for some classical constants via analytic continuations of Lerch’s transcendent. Ramanujan J 16, 247–270 (2008).

$$I_n:=\int_0^1\left(1-\sqrt{x}\right)^ndx=\frac{2}{(n+1)(n+2)}$$where we substitute $y=x^2$ and use the beta function.

ex)$$\int_0^1\left(1-\sqrt{x}\right)^{19}dx=\frac{1}{210}$$

REFERENCE:

P.J.Nahin(2015)は面白い積分テクニックがたくさん載った人気書籍です！

Inside Interesting Integrals【楽天】

Inside Interesting Integrals【amazon】

$$y'=x+y^2$$

１階非線型微分方程式の例

By termwise integration we obtain$$(m-1)\int_0^1\sum_{n=1}^\infty x^{m^n-1}dx=1$$

\begin{align}\frac{d}{dt}\left\{\Li_2\left(\frac{2t}{1+t^2}\right)\right\}&=-\frac{(1-t^2)\ln\frac{(1-t)^2}{1+t^2}}{t(1+t^2)}\\&=\frac{4t\ln(1-t)}{1+t^2}-\frac{2t\ln(1+t^2)}{1+t^2}-\frac{2\ln(1-t)}{t}+\frac{\ln(1+t^2)}{t}\end{align}$0$ から $x$ まで積分して$(x\le 1)$\begin{align}\Li_2\left(\frac{2x}{1+x^2}\right)&=4\int_0^x\frac{t\ln(1-t)}{1+t^2}dt-\underbrace{2\int_0^x\frac{t\ln(1+t^2)}{1+t^2}dt}_{t^2=u}\\&\quad -2\int_0^x\frac{\ln(1-t)}{t}dt+\underbrace{\int_0^x\frac{\ln(1+t^2)}{t}dt}_{-t^2=u}\\&=4\int_0^x\frac{t\ln(1-t)}{1+t^2}dt-\frac{1}{2}\ln^2(1+x^2)+2\Li_2(x)-\frac{1}{2}\Li_2(-x^2)\end{align}よって$$\int_0^x\frac{t\ln(1-t)}{1+t^2}dt=\frac{1}{4}\Li_2\left(\frac{2x}{1+x^2}\right)+\frac{1}{8}\ln^2(1+x^2)-\frac{1}{2}\Li_2(x)+\frac{1}{8}\Li_2(-x^2)$$特に $x=1$ では$$\int_0^1\frac{t\ln(1-t)}{1+t^2}dt=\frac{1}{8}\ln^22-\frac{5}{16}\zeta(2)$$

参考文献：Cornel Ioan Vălean, "More (Almost) Impossible Integrals, Sums, and Series" ,　楽天はこちら

$$\int_0^\pi \t^2\ln^3\sin\t d\t=-\left[\frac{3}{2}\pi\zeta(5)+\frac{13}{120}\pi^5\ln2+\frac{5}{8}\pi^3\zeta(3)+\frac{3}{2}\pi\zeta(3)\ln^22+\frac{1}{3}\pi^3\ln^32\right]$$PROOF.
From here we define\begin{align}I(s,a)&:=\int_0^\pi\sin^{s-1}\t\cos a\t d \t=\frac{\pi\cos\frac{\pi a}{2}}{2^{s-1}sB(\frac{s+a+1}{2},\frac{s-a+1}{2})}\\&\Longrightarrow\frac{\partial^2}{\partial a^2}\left(\left.\frac{\partial^3I}{\partial s^3}\right|_{s=1}\right)_{a=0}=-\int_0^\pi \t^2\ln^3\sin\t d\t\end{align}The third derivative of $I$ with respect to $s$ is\begin{align}\frac{\partial^3I}{\partial s^3}&=I(s,a)\left[f(s,a)^3+3f(s,a)g(s,a)+h(s,a)\right]\\\left.\frac{\partial^3I}{\partial s^3}\right|_{s=1}&=\frac{\sin\pi a}{a}\left[\a^3+3\a\b+\d\right]\end{align}where\begin{align}f(s,a)&=\psi(s)-\ln2-\frac{1}{2}\psi\left(\frac{s+a+1}{2}\right)-\frac{1}{2}\psi\left(\frac{s-a+1}{2}\right)\\g(s,a)&=\psi'(s)-\frac{1}{4}\psi'\left(\frac{s+a+1}{2}\right)-\frac{1}{4}\psi'\left(\frac{s-a+1}{2}\right)\\h(s,a)&=\psi''(s)-\frac{1}{8}\psi''\left(\frac{s+a+1}{2}\right)-\frac{1}{8}\psi''\left(\frac{s-a+1}{2}\right)\\\a(a)&=f(1,a)\\\b(a)&=g(1,a)\\\d(a)&=h(1,a)\end{align}Differentiating twice with respect to $a$ gives\begin{align}\frac{\partial^2}{\partial a^2}\left(\left.\frac{\partial^3I}{\partial s^3}\right|_{s=1}\right) &=\underbrace{\frac{(2-\pi^2a^2)\sin\pi a-2\pi a\cos\pi a}{a^3}}_{\to -\frac{\pi^3}{3}\:(a\to 0)}(\a^3+3\a\b+\d)\\&\quad+2\underbrace{\frac{\pi a\cos\pi a-\sin\pi a}{a^2}}_{\to 0\:(a\to 0)}(3\a^2\a'+3\a'\b+3\a\b'+\d')\\&\quad+\frac{\sin\pi a}{a}(3\a^2\a''+6\a\a'^2+3\a''\b+6\a'\b'+3\a\b''+\d'')\end{align}Then we put $a=0$ to have the result above, with the help of\begin{align}\a(0) &=-\ln2,\quad \b(0)=\frac{1}{2}\zeta(2),\quad \d(0)=-\frac{3}{2}\zeta(3)\\\a'(0)&=\b'(0)=\d'(0)=0\\\a''(0) &=\frac{1}{2}\zeta(3),\quad \b''(0)=-\frac{3}{4}\zeta(4),\quad \d''(0)=\frac{3}{2}\zeta(5)\end{align}

$$\cfrac{\displaystyle\int_2^{17}\cfrac{dx}{\sqrt{x^3-7x+6}}}{\displaystyle\int_2^{3}\cfrac{dx}{\sqrt{x^3-7x+6}}}=2$$PROOF.
Setting $$x=2\frac{t^4+2t^3+14t^2-62t+61}{(t^2-4t-1)^2}$$yields\begin{align}\int_2^{17}\cfrac{dx}{\sqrt{x^3-7x+6}}&=-\int_2^3\sqrt{\frac{(t^2-4t-1)^6}{100(t^3-7t+6)(t^2-2t+5)^2(t^2+6t-11)^2}}\\&\quad\quad\cdot\frac{20(t^2-2t+5)(t^2+6t-11)}{(t^2-4t-1)^3}dt\\&=2\int_2^{3}\cfrac{dt}{\sqrt{t^3-7t+6}}\end{align}