この積分はフレネル積分とよばれており、複素解析を用いることで求めることができる。コーシーの積分定理を使うなどの複素積分の練習としてもうってつけである。
2つの定積分$$I=\int^\infty_0\cos (x^2)dx$$$$J=\int^\infty_0\sin (x^2)dx$$ の値はいくらか．
これはフレネル積分といわれるものの上端を無限大としたものです。複素解析の手法で計算することができます。
まず$$\oint_C e^{iz^2}dz$$なる複素積分を考えます。ここで閉曲線 $C$ は図のような半径 $R$ の扇形です（半径が1になっていますが目盛りは無視して下さい）。
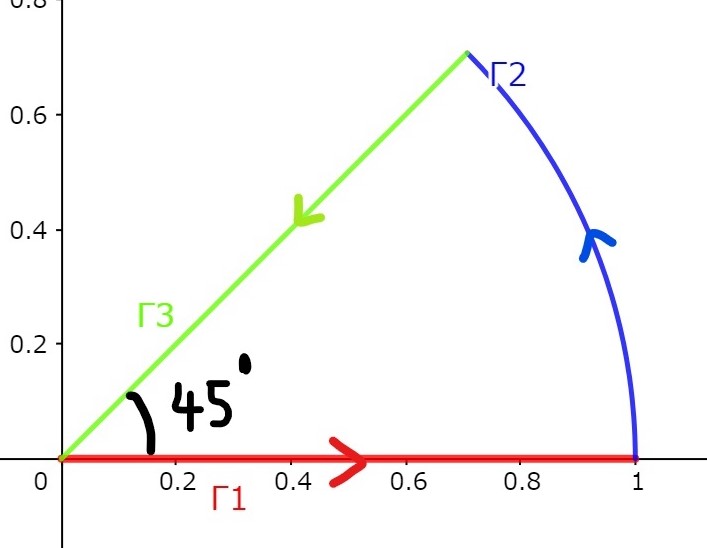
被積分関数は閉曲線内で極をもたないためコーシーの積分定理より、この周回積分は $0$ となります。$$\oint_C e^{iz^2}dz=0$$周回積分を３つに分けて$$0=\oint_Ce^{iz^2}dz=\int^R_0e^{ix^2}dx+\int_{\Gamma_2}e^{iz^2}dz+\int_{\Gamma_3}e^{iz^2}dz$$右辺第1項は$\Gamma_1$に関する積分のことです。以下、問題形式で進めていきます。
$\Gamma_2$の線積分において，$z=Re^{i\theta}$ と置換し，$R\to\infty$ としたときの積分値を計算せよ．
置換してみると $e$ の $e$ 乗が出てくるので、そこは三角関数に直してやります。\begin{eqnarray*}\int_{\Gamma_2}e^{iz^2}dz &=& iR\int^{\frac{\pi}{4}}_0e^{i\theta}e^{iR^2(\cos2\theta+i\sin2\theta)}d\theta\\&=& iR\int^{\frac{\pi}{4}}_0e^{i\theta}e^{R^2(i\cos2\theta-\sin2\theta)}d\theta\end{eqnarray*}さて、この結果の絶対値をとって評価すると\begin{eqnarray*}\left| iR\int^{\frac{\pi}{4}}_0e^{i\theta}e^{R^2(i\cos2\theta-\sin2\theta)}d\theta \right| &=& R\left| \int^{\frac{\pi}{4}}_0e^{i\theta}e^{iR^2\cos2\theta}e^{-R^2\sin2\theta}d\theta \right|\\ &\leq & R\int^{\frac{\pi}{4}}_0\left| e^{i\theta}e^{iR^2\cos2\theta}e^{-R^2\sin2\theta}\right| d\theta\\ &=& R \int^{\frac{\pi}{4}}_0\left| e^{-R^2\sin2\theta}\right| d\theta\xrightarrow[R\to\infty]{}0\end{eqnarray*}よって求める積分値は$0$となります。
$\Gamma_3$の線積分において，$z=e^{i\frac{\pi}{4}}x$ と置換し，$R\to\infty$ としたときの積分値を計算せよ．
置換したときに$x$がどのような範囲になるか注意します。$z^2=e^{i\frac{\pi}{2}}x^2=ix^2$ より\begin{eqnarray*}\int_{\Gamma_3}e^{iz^2}dz &=& \int^0_Re^{-x^2}\cdot e^{\frac{\pi}{4}i}dx\ &\xrightarrow[R\to\infty]{}& -e^{\frac{\pi}{4}i}\int^\infty_0e^{-x^2}dx\\ &=& -e^{\frac{\pi}{4}i}\cdot \frac{\sqrt{\pi}}{2}\end{eqnarray*}これで$\Gamma_3$ の積分が終わりました。
仕上げになります。周回積分の３分割を再度示すと$$0=\oint_Ce^{iz^2}dz=\int^R_0e^{ix^2}dx+\int_{\Gamma_2}e^{iz^2}dz+\int_{\Gamma_3}e^{iz^2}dz$$
$R\to\infty$ とし、$\Gamma_2$ と $\Gamma_3$ の積分値を代入すると$$0=\int^\infty_0e^{ix^2}dx+0-e^{\frac{\pi}{4}i}\cdot \frac{\sqrt{\pi}}{2}$$すなわち$$\int^\infty_0e^{ix^2}dx=\sqrt{\frac{\pi}{8}}(1+i)$$これの実部と虚部を比べると下の結論を得ます。
$$\int^\infty_0\cos (x^2)dx=\sqrt{\frac{\pi}{8}}$$$$\int^\infty_0\sin (x^2)dx=\sqrt{\frac{\pi}{8}}$$
これでおしまいです。
今回は三角関数の引数が2乗になっているケースを考察しました。これを応用して、3乗・4乗・5乗・・・そして$n$乗もやってみました！
【複素解析】cos(x^3),sin(x^3)の積分(扇形周回積分とガンマ関数)
【複素解析】cos(x^n),sin(x^n) の定積分（フレネル積分を一般化）
Please support me!
記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。
