Previous posts:
Integrals and Miscellaneous 18
Integrals and Miscellaneous 17
Integrals and Miscellaneous 16
Integrals and Miscellaneous 15
Integrals and Miscellaneous 14
Integrals and Miscellaneous 13
Integrals and Miscellaneous 12
Integrals and Miscellaneous 11
Integrals and Miscellaneous 10
$$\sqrt[3]{2+11i}+\sqrt[3]{2-11i}=4$$
Can we test the convergence of infinite products with the convergence of series ?$$P:=\prod_{n=1}^\infty (1+z_n)\quad ,\quad S:=\sum_{n=1}^\infty z_n$$then\begin{eqnarray*}P:\mathrm{absolutely\: convergent}&\Longleftrightarrow& S:\mathrm{absolutely\: convergent}\\P:\mathrm{conditionally\: convergent}&\nLeftrightarrow& S:\mathrm{conditionally\: convergent}\\P:\mathrm{divergent}&\nLeftrightarrow& S:\mathrm{divergent}\end{eqnarray*}
From @SrinivasR1729
$$S:=\sum_{n=0}^\infty\frac{(8n+1)!!}{(8n+2)!!(2n+1)(8n+1)}=\frac{2}{3}\left(\sqrt{2}-\sqrt{\sqrt{2}-1}\right)$$PROOF.\begin{eqnarray*}S &=& \frac{1}{2}\sum_{n=0}^\infty \frac{(\frac{1}{8})_n(\frac{3}{8})_n(\frac{5}{8})_n(\frac{7}{8})_n}{(\frac{3}{4})_n(\frac{5}{4})_n(\frac{3}{2})_n n!} \\&=&\frac{1}{2}{}_4F_3\left[\begin{matrix}\frac{1}{8},\frac{3}{8},\frac{5}{8},\frac{7}{8}\\\frac{3}{4},\frac{5}{4},\frac{3}{2}\end{matrix};1\right]\end{eqnarray*}Exton[1] deduced (and Brychkov[2] corrected) that$${}_4F_3\left[\begin{matrix}\frac{a+1}{2},\frac{a}{2}+1,\frac{b+1}{2},\frac{b}{2}+1\\\frac{a-b}{2}+1,\frac{a-b+3}{2},\frac{3}{2}\end{matrix};1\right]=\frac{1}{2ab}\left(\frac{\G(2+a-b)\G(1-2b)}{\G(1-b)\G(1+a-2b)}-\frac{\G(2+a-b)\G(1+\frac{a}{2}}{\G(1+a)\G(1+\frac{a}{2}-b)}\right)$$where $\mathfrak{R}b<\frac{1}{2}$. Substituting $a=-\frac{3}{4}$ , $b=-\frac{1}{4}$ yields$${}_4F_3\left[\begin{matrix}\frac{1}{8},\frac{3}{8},\frac{5}{8},\frac{7}{8}\\\frac{3}{4},\frac{5}{4},\frac{3}{2}\end{matrix};1\right]=\frac{4}{3}\left(\sqrt{2}-\sqrt{\sqrt{2}-1}\right)$$Hence,$$\sum_{n=0}^\infty\frac{(8n+1)!!}{(8n+2)!!(2n+1)(8n+1)}=\frac{2}{3}\left(\sqrt{2}-\sqrt{\sqrt{2}-1}\right)$$
[1] H.Exton(1997), Some new summation formulae for the generalised hypergeometric function of higher order
[2] Yury Brychkov, Handbook of Special Functions: Derivatives, Integrals, Series and Other Formulas
From @6ahRJ6PeIkQWmsk$$I:=\int_0^\infty\frac{\sin x\ln x}{x}dx=-\frac{\g\pi}{2}$$PROOF.$$f(z):=\frac{e^{iz}\ln z}{z}$$We consider the $z$-plane whose negative imaginary axis is the brunch cut ($-\frac{\pi}{2}<\arg z<\frac{3}{2}\pi$).
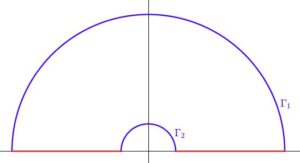
There is no singularity in the above contour then\begin{eqnarray*}0 &=& \int_\infty^\epsilon\frac{e^{-ix}(\ln x+i\pi)}{-x}(-dx)+ \int_\pi^0 e^{i\epsilon e^{i\t}}(\ln\epsilon+i\t) id\t \\&&+\int_\epsilon^\infty\frac{e^{ix}\ln x}{x}dx+\int_0^\pi e^{iRe^{i\t}}(\ln R+i\t )id\t\\&=& 2i\: I-i\pi\int_\epsilon^\infty\frac{e^{-ix}}{x}dx -i\int_0^\pi e^{i\epsilon e^{i\t}}(\ln\epsilon+i\t) d\t +i\int_0^\pi e^{iRe^{i\t}}(\ln R+i\t )d\t\\&=& 2i\: I-i\pi\left(-\mathrm{Ci}(\epsilon)-i\frac{\pi}{2}\right) -i\pi\ln\epsilon+\frac{\pi^2}{2} +i\int_0^\pi e^{iRe^{i\t}}(\ln R+i\t )d\t\\&=&2i\: I+i\pi\mathrm{Ci}(\epsilon)-i\pi\ln\epsilon+i\int_0^\pi e^{iRe^{i\t}}(\ln R+i\t )d\t\end{eqnarray*}The last term is\begin{eqnarray*}\left|\int_0^\pi e^{iRe^{i\t}}(\ln R+i\t )d\t\right| &\le&\int_0^\pi e^{-R\sin\t}(\ln R+\t)d\t \le(\ln R+\pi)\int_0^\pi e^{-R\sin\t}d\t \\&=& \frac{\ln R+\pi}{2}\int_0^\frac{\pi}{2} e^{-R\sin\t}d\t \le\frac{\ln R+\pi}{2}\int_0^\frac{\pi}{2} e^{-\frac{2R}{\pi}\t}d\t \\&=&\frac{\ln R+\pi}{2}\frac{\pi}{2R}(1-e^{-R}) \rightarrow 0\end{eqnarray*}From $\mathrm{Ci}(x)=\g+\ln x +O(x^2)$ it follows that$$\int_0^\infty\frac{\sin x\ln x}{x}dx=-\frac{\g\pi}{2}$$REFERENCE:
Abramowitz, M., Stegun, I. A. (1964). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover. 【楽天はココ】
From @nasya_tw $$I:=\int_0^{3^{-1/3}}\frac{dx}{(1-x^6)^\frac{2}{3}}=\frac{\G^3(\frac{1}{3})}{2^\frac{7}{3}\sqrt{3}\pi}$$PROOF.\begin{eqnarray*}I &=& \int_0^{3^{-1/3}}\sum_{n=0}^\infty\frac{(\frac{2}{3})_n}{n!}x^{6n}dx\\&=&\frac{1}{3^{1/3}}\sum_{n=0}^\infty \frac{(\frac{2}{3})_n}{n!(6n+1)9^n}\\&=&\frac{1}{3^{1/3}} F\left[\begin{matrix}\frac{2}{3},\frac{1}{6}\\\frac{7}{6}\end{matrix};\frac{1}{9}\right]\end{eqnarray*}Recall the formula$$F\left[\begin{matrix}2s,\frac{1}{2}-s\\s+\frac{5}{6}\end{matrix};\frac{1}{9}\right]=\frac{3^{s}\G(s+\frac{5}{6})\G(\frac{2}{3})}{4^{s}\G(s+\frac{2}{3})\G(\frac{5}{6})}$$ which we deduced here. Setting $s=1/3$ yields$$I=\frac{\G^3(\frac{1}{3})}{2^\frac{7}{3}\sqrt{3}\pi}$$
\begin{eqnarray}\sum_{n=1}^\infty\frac{H_n^2}{n(n+1)}x^n &=& \Li_3(x)-\frac{2\Li_3(1-x)}{x}+\left(\frac{1}{x}-1\right)\ln(1-x)\Li_2(x)+\left(\frac{1}{x}-1\right)\frac{\ln^3(1-x)}{3}\\&&+\frac{2}{x}\ln(1-x)\Li_2(1-x)+\frac{\ln x\ln^2(1-x)}{x}+\frac{2\zeta(3)}{x}\end{eqnarray}$$\sum_{n=1}^\infty\frac{H_n^2}{n(n+1)2^n}=\frac{11}{8}\zeta(3)-\frac{\pi^2}{6}\ln 2-\frac{\ln^32}{3}$$$$\sum_{n=1}^\infty\frac{H_n^2}{n(n+1)}=3\zeta(3)$$
【8】整関数とワイエルシュトラスの因数分解定理①(基本乗積・種数)
$$f(z)=z^m e^{g(z)}\prod_{n=1}^\infty \left(1-\frac{z}{\lambda_n}\right)e^{\frac{z}{\lambda_n}+\frac{z^2}{2\lambda_n^{~2}}+\cdots\frac{z^{k_n}}{k_n\lambda_n^{~k_n}}}$$
$$\sum_{n=1}^\infty\frac{(a)_n}{n!}H_nx^n=-(1-x)^{-a}\ln\frac{1-x}{x}+\{\psi(a)+\g\}(1-x)^{-a}+\frac{1}{a}F\left[\begin{matrix}1,a\\1+a\end{matrix};1-x\right]$$$$\therefore\quad \sum_{n=0}^\infty\frac{(\frac{1}{2})_n}{n!}H_nx^n=\frac{2}{\sqrt{1-x}}\ln\frac{1+\sqrt{1-x}}{2\sqrt{1-x}}$$$$\sum_{n=0}^\infty\frac{(\frac{1}{2})_n}{n!}(2H_{2n}-H_n)x^{n}=-\frac{\ln(1-x)}{\sqrt{1-x}}$$
$$f(z)=g(z)\left(\frac{z}{R}\right)^m\prod_{n=1}^\infty \frac{|a_n|}{a_n}\frac{R(z-a_n)}{\bar{a_n}z-R^2}$$
$$\int_a^{a+1}\ln\G(x)dx=a\ln a-a+\frac{\ln2\pi}{2}$$
Brafman's generating functions$${}_2F_1\left[\begin{matrix}c,1-c\\1\end{matrix};\frac{1-t-\rho}{2}\right]{}_2F_1\left[\begin{matrix}c,1-c\\1\end{matrix};\frac{1+t-\rho}{2}\right]=\sum_{n=0}^\infty\frac{(c)_n(1-c)_nP_n(x)}{n!^2}t^n$$where $\rho=(1-2xt+t^2)^{1/2}$.
[1] Brafman, F. (1951). Generating functions of Jacobi and related polynomials. Proceedings of the American Mathematical Society, 2(6), 942–949.
[2] Rainville, E.D. (1960) Special Functions. The Macmillan Company, New York.
Machin's formula$$\frac{\pi}{4}=4\arctan\left(\frac{1}{5}\right)-\arctan\left(\frac{1}{239}\right)$$Euler's formula$$\frac{\pi}{4}=\arctan\left(\frac{1}{2}\right)+\arctan\left(\frac{1}{3}\right)$$Hermann's formula$$\frac{\pi}{4}=2\arctan\left(\frac{1}{2}\right)-\arctan\left(\frac{1}{7}\right)$$Hutton's formula$$\frac{\pi}{4}=2\arctan\left(\frac{1}{3}\right)+\arctan\left(\frac{1}{7}\right)$$Euler's formula$$\pi=20\arctan\left(\frac{1}{7}\right)+8\arctan\left(\frac{3}{79}\right)$$Dase's formula(?)$$\frac{\pi}{4}=\arctan\left(\frac{1}{2}\right)+\arctan\left(\frac{1}{5}\right)+\arctan\left(\frac{1}{8}\right)$$Ferguson's formula(?)$$\frac{\pi}{4}=3\arctan\left(\frac{1}{4}\right)+\arctan\left(\frac{1}{20}\right)+\arctan\left(\frac{1}{1985}\right)$$Shanks-Wrench(?)$$\pi=24\arctan\left(\frac{1}{8}\right)+8\arctan\left(\frac{1}{57}\right)+4\arctan\left(\frac{1}{239}\right)$$
[1] Borwein & Borwein, Pi and the AGM, 340-345p
Next:
Integrals and Miscellaneous 20
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。





