「ガンマ関数の基礎」シリーズ第8回。これまでガンマ関数の微分を扱ったことがありましたが、そのときに現れた「ディガンマ関数」に焦点を当て、詳しくみていきます。ガンマ関数 $\G(z)$が「積」のイメージだとすると、ディガンマ関数 $\psi(z)$ は「和」のイメージです。
ガンマ関数については「相反公式」「倍数公式」などの関係式を導いたほか、微分したり級数表示したり特殊値を求めたりしました。今回からしばらくはディガンマ関数について同様のことをやります。
本記事とはあまり関係ありませんが、前回の記事:
ディガンマ関数を用いた過去記事はこちら(読まなくても今回の記事は理解できます):
もくじ
ディガンマの漸化式
ディガンマ関数 $\psi(z)$ はガンマ関数の対数微分として定義されます。
\begin{equation}\psi(z)\equiv\frac{\G'(z)}{\G(z)}\tag{1}\end{equation}
ガンマ関数の漸化式 $\G(z+1)=z\G(z)$ の対数微分をとることで、ディガンマ関数の重要な漸化式を得ます。ただし $z\neq 0,-1,-2\cdots$ です。
\begin{equation}\psi(z+1)=\psi(z)+\frac{1}{z}\tag{2}\end{equation}
漸化式が得られるのはありがたいですが、それなら「初項」みたいなものも欲しいですね。次に $\psi(1)$ を考えましょう。
オイラー・マスケローニ定数と $\psi(1)$
ガンマ関数に関するガウスの公式$$\frac{1}{\G(z)}=\displaystyle\lim_{n\to\infty}\frac{\prod_{k=0}^n(z+k)}{n!n^z}$$の両辺の対数をとって微分すると$$-\frac{\G'(z)}{\G(z)}=\displaystyle\lim_{n\to\infty}\left[\frac{1}{z}+\frac{1}{z+1}+\cdots+\frac{1}{z+n}-\log n\right]$$よって(1)より
\begin{equation}\psi(z)=-\displaystyle\lim_{n\to\infty}\left[\frac{1}{z}+\frac{1}{z+1}+\cdots+\frac{1}{z+n}-\log n\right]\tag{3}\end{equation}
ガンマ関数が無限乗積の形で表されたのに対し、こちらは無限和となっていますね。ここで $z=1$ とすると$$\psi(1)=-\displaystyle\lim_{n\to\infty}\left[1+\frac{1}{2}+\cdots+\frac{1}{1+n}-\log n\right]$$$$\therefore\quad\psi(1)=-\displaystyle\lim_{n\to\infty}\left[\left(\sum_{k=1}^n\frac{1}{k}-\log n\right)+\left(\frac{1}{n+1}\right)\right]$$リミットの中の第1項は収束して「オイラー・マスケローニ定数」とよばれます。
\begin{equation}\gamma\equiv\displaystyle\lim_{n\to\infty}\left(\sum_{k=1}^n\frac{1}{k}-\log n\right)\approx 0.577\tag{4}\end{equation}
第2項 $\frac{1}{n+1}$ もゼロに収束しますから$$\psi(1)=-\g$$と求まります。新しい定数を導入しただけなので「求まった」といえるかは分かりませんが,ガンマ関数に関する話ではこの定数が頻出します。$\pi$ と同様に当たり前のように使っていきましょう。
なお、数列が収束して値をとることの証明は以下の記事の「追記」を見てください:
自然数における $\psi(z)$ の値
以上から $\psi(z)$ の式をまとめると
$$\psi(1)=-\g$$$$\psi(z+1)=\psi(z)+\frac{1}{z}$$
これより$$\begin{cases}\psi(1)&=&-\g\\\psi(2)&=&1-\g\\\psi(3)&=&\dfrac{3}{2}-\g\\&\vdots&\\\\\psi(n)&=&-\g+h_{n-1}\end{cases}$$ただし $h_n$ は「調和数」で$$h_n\equiv\sum_{k=1}^{n}\frac{1}{k}\;,\; h_0=1$$と定義されます。
\begin{equation}\psi(n)=-\g+h_{n-1}\quad(n\in\NN)\tag{5}\end{equation}
本記事では、下記の本を参考にしています。2021年8月現在、第30刷。かなりの廉価ながら特殊関数に関する公式が網羅されています。参照用にするもよし、公式の証明にトライするもよし。

【Amazon】特殊函数 (岩波 数学公式 3)
(2)や(3)から分かるように $\psi(z)$ は $z=0,-1,-2\cdots$ で発散し、値をもちません。$\psi(z)$ は $z=0,-1,-2\cdots$ で1位の極をもつのです。それを示します。
\begin{eqnarray*}\displaystyle\lim_{z\to 0}z\psi(z)&=&\displaystyle\lim_{z\to 0}z\left(\psi(z+1)-\frac{1}{z}\right)\\&=&\displaystyle\lim_{z\to 0}\left(z\psi(z+1)-1\right)\\&=&-1\end{eqnarray*}
\begin{eqnarray*}\displaystyle\lim_{z\to -1}(z+1)\psi(z)&=&\displaystyle\lim_{z\to -1}(z+1)\left(\psi(z+1)-\frac{1}{z}\right)\\&=&\displaystyle\lim_{z\to -1}\left((z+1)\psi(z+1)-\frac{z+1}{z}\right)\\&=&\displaystyle\lim_{z\to 0}\left(z\psi(z)-\frac{z}{z-1}\right)\\&=&-1\end{eqnarray*}よって $z=0,-1$ で1位の極をもち、その留数 $a_{-1}=-1$ です。一般の自然数 $n$ についても\begin{eqnarray*}\displaystyle\lim_{z\to -n}(z+n)\psi(z)&=&\displaystyle\lim_{z\to -n}(z+n)\left(\psi(z+1)-\frac{1}{z}\right)\\&=&\displaystyle\lim_{z\to -n}\left((z+n)\psi(z+1)-\frac{z+n}{z}\right)\\&=&\displaystyle\lim_{z\to -n}(z+n)\psi(z+1)\\&=&\displaystyle\lim_{z\to -n}(z+n)\psi(z+2)\\&\vdots&\\&=&\displaystyle\lim_{z\to -n}(z+n)\psi(z+n)\\&=&-1\end{eqnarray*}やはり1位の極で留数 $-1$ となりました。
$\psi(z)$ は $z=0,-1,-2\cdots$ で1位の極をもち、それぞれの点での留数は $-1$ である。
(3)式を再掲します。
\begin{equation}\psi(z)=-\displaystyle\lim_{n\to\infty}\left[\frac{1}{z}+\frac{1}{z+1}+\cdots+\frac{1}{z+n}-\log n\right]\tag{6}\end{equation}
これを変形します。\begin{eqnarray*}\psi(z)&=&\displaystyle\lim_{n\to\infty}\left[\log n-\sum_{k=0}^n\frac{1}{z+k}\right]\\&=&-\g+\displaystyle\lim_{n\to\infty}\left[\log n+\g-\sum_{k=0}^n\frac{1}{z+k}\right]\\&=&-\g-\sum_{n=0}^\infty\left(\frac{1}{z+n}-\frac{1}{n+1}\right)\end{eqnarray*}したがって次の表示を得ます。
\begin{equation}\psi(z)=-\g-\sum_{n=0}^\infty\left(\frac{1}{z+n}-\frac{1}{n+1}\right)\tag{7}\end{equation}
(6)と比べるとかなり見やすくなったのではないでしょうか。ディガンマ関数にはほかにも、ゼータ関数を使った級数表示など面白い公式があります。参考記事:
【γ9】ディガンマ関数の相反公式・倍数公式と特殊値・ゼータ関数(ガンマ関数の基礎シリーズ9)
$z$ が自然数のときのディガンマ関数の値は分かりましたが、非整数ではどうでしょうか。例えば(7)から\begin{eqnarray*}\psi\left(\frac{1}{2}\right)&=&-\g-\sum_{n=0}^\infty\left(\frac{1}{\frac{1}{2}+n}-\frac{1}{n+1}\right)\\&=&-\g-2\sum_{n=0}^\infty\left(\frac{1}{2n+1}-\frac{1}{2n+2}\right)\\&=&-\g-2\left(1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\cdots\right)\\&=&-\g-2\log 2\end{eqnarray*}のように求めることができます。すると漸化式$$\psi(z+1)=\psi(z)+\frac{1}{z}$$から半整数の値がことごとく分かります。$$\begin{cases}\psi\left(\dfrac{3}{2}\right)&=&-\g-2\log 2+2\\\psi\left(\dfrac{5}{2}\right)&=&-\g-2\log 2+\frac{8}{3}\end{cases}$$より一般的には、自然数 $n$ に対して以下の式が成立します。
\begin{equation}\psi\left(\frac{1}{2}\pm n\right)=-\g-2\log2+2\sum_{k=1}^n\frac{1}{2k-1}\tag{8}\end{equation}
$z=1/3$ などについても考察済みなので、次回以降の記事で書いていきます。
ちなみに $\psi(z)$ はgeogebraに実装済みの関数で、「psi(x)」と入力すれば下図のようになります。
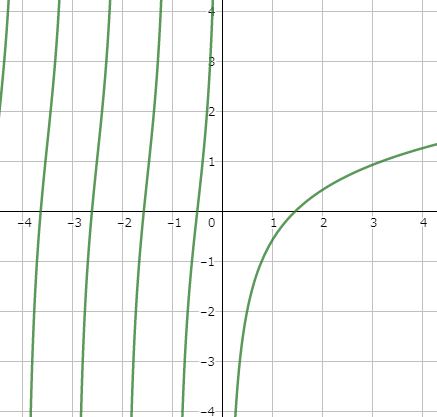
$$\displaystyle\lim_{x\to -n}\frac{\psi(x)}{\G(x)} \quad(n\in\ZZ^+)$$
$\G(x)$ と $\psi(x)$ は ともに $x=0,-1,-2\cdots$ で1位の極をもちますので、意味のある値が得られそうな気がしますね。そこで\begin{eqnarray*}\displaystyle\lim_{x\to 0}\frac{\psi(x)}{\G(x)}&=&\displaystyle\lim_{x\to 0}\frac{x\psi(x)}{x\G(x)}\\&=&\displaystyle\lim_{x\to 0}\frac{x[\psi(x+1)-\frac{1}{x}]}{\G(x+1)}\\&=&\displaystyle\lim_{x\to 0}\frac{x\psi(x+1)-1}{\G(x+1)}\end{eqnarray*}\begin{equation}\therefore\quad\displaystyle\lim_{x\to 0}\frac{\psi(x)}{\G(x)}=-1\tag{A}\end{equation}さらに負整数については $n\in\NN$ として\begin{eqnarray*}\displaystyle\lim_{x\to -n}\frac{\psi(x)}{\G(x)}&=&\displaystyle\lim_{x\to 0}\frac{\psi(x-n)}{\G(x-n)}\\&=&\displaystyle\lim_{x\to 0}\frac{(x-n)\psi(x-n)}{\G(x-n+1)}\\&=&\displaystyle\lim_{x\to 0}\frac{(x-n)[\psi(x-n+1)-\frac{1}{x-n}]}{\G(x-n+1)}\\&=&\displaystyle\lim_{x\to 0}\frac{(x-n)\psi(x-n+1)-1}{\G(x-n+1)}\\&=&\displaystyle\lim_{x\to 0}\left[(x-n)\frac{\psi(x-n+1)}{\G(x-n+1)}-\frac{1}{\G(x-n+1)}\right]\\&=&\displaystyle\lim_{x\to 0}(x-n)\frac{\psi(x-n+1)}{\G(x-n+1)}\\&=&\displaystyle\lim_{x\to -(n-1)}(x-1)\frac{\psi(x)}{\G(x)}\\&=&-n\displaystyle\lim_{x\to -(n-1)}\frac{\psi(x)}{\G(x)}\end{eqnarray*}繰り返して最後に(A)を利用すれば$$\therefore\quad\displaystyle\lim_{x\to -n}\frac{\psi(x)}{\G(x)}=n!(-1)^{n-1}\quad(n\in\ZZ^+)$$
次回:
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。


