前回:
の続きです。
3つのヤコビの楕円関数の定義域を、周期性や加法定理に注目して複素数全体にまで拡張します。さらに半角の公式や倍角の公式を導出し、三角関数や双曲線関数との類似性を確認します。
前回導出したように、3つのヤコビの楕円関数に関する加法定理は
\begin{eqnarray}\mathrm{sn}(u+v)&=&\frac{\sn u\:\cn v\:\dn v+\sn v\:\cn u\:\dn u}{1-k^2\mathrm{sn}^2u\:\mathrm{sn}^2v}\tag{1a}\\\mathrm{cn}(u+v)&=&\frac{\cn u\:\cn v-\sn u\:\sn v\:\dn u\:\dn v}{1-k^2\mathrm{sn}^2u\:\mathrm{sn}^2v}\tag{1b}\\\mathrm{dn}(u+v)&=&\frac{\dn u\:\dn v-k^2\sn u\:\sn v\:\cn u\:\cn v}{1-k^2\mathrm{sn}^2u\:\mathrm{sn}^2v}\tag{1c}\end{eqnarray}
$\sn u$ は奇関数、$\cn u$ , $\dn u$ は偶関数です。
第1種不完全楕円積分の逆関数として $\sn u$ を定義したため、3つの関数の定義域は $u\in [-K,K]$ なのでした。しかし $\sn$ は $\sin$ に、$\cn$は $\cos$ に似ており、定義域を周期的に広げられそうに見えるという話もしました。
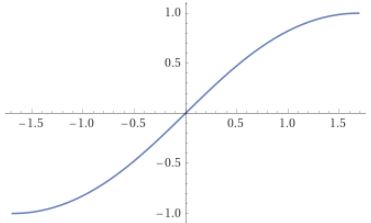
実際に加法定理によって、定義域を実数全体へ拡張しましょう。命題21と定理27より$$\mathrm{sn}(u\pm K) = \pm\frac{\cn u}{\dn u}$$これによって $\sn u$ の定義域を $[-2K,2K]$ へ拡張できます。また明らかに $\sn 2K=0$ であり、これを定理27へ用いると$$\mathrm{sn}(u\pm 2K) =-\sn u $$よって $u$ に $u\pm 2K$ を代入すると$$\mathrm{sn}(u\pm 4K)=\sn u$$すなわち周期 $4K$ の関数として実数全体に拡張できることになります。
$k=0$ の場合 $K(0)=\frac{\pi}{2}$ であり、$\mathrm{sn}(u,0)=\sin u$ なのでした。上記の周期性は $\sin u$ の周期性と辻褄が合います。
このように進めると、次のようにまとまります。
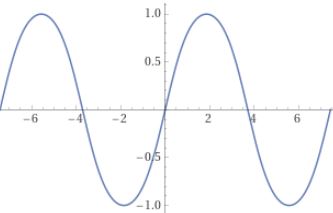
\begin{align}\mathrm{sn}(u\pm K) &= \pm\frac{\cn u}{\dn u} & \mathrm{cn}(u\pm K) &=\mp k'\frac{\sn u}{\dn u} & \mathrm{dn}(u\pm K) &= \frac{k'}{\dn u}\\\mathrm{sn}(u\pm 2K) &= -\sn u & \mathrm{cn}(u\pm 2K) &=-\cn u & \mathrm{dn}(u\pm 2K) &= \dn u\\\mathrm{sn}(u\pm 4K) &= \sn u & \mathrm{cn}(u\pm 4K) &=\cn u & &\end{align}
\begin{align}\sn 0 &= 0 & \cn 0 &=1 & \dn 0 &= 1\\\sn K &= 1 & \cn K &=0 & \dn K &= k'\\\sn 2K &= 0 & \cn 2K &=-1 & \dn 2K &= 1\\\sn 3K &= -1 & \cn 3K &=0 & \dn 3K &= k'\\\sn 4K &= 0 & \cn 4K &=1 & \dn 4K &= 1\end{align}
$\sn u$ , $\cn u$ は周期 $4K$ であり、$\dn u$ の周期は $2K$ です。なお複素数へ拡張した場合、それぞれもう1つ周期をもちますが、それは今後の記事で紹介する予定です。
加法定理から直ちに導かれるとはいえ、倍角の公式を書いておいて損はないでしょう。
\begin{align}\sn 2u&=\frac{2\sn u\:\cn u\:\dn u}{1-k^2\mathrm{sn}^4u}\\\cn 2u &=\frac{1-2\mathrm{sn}^2 u+k^2\mathrm{sn}^4u}{1-k^2\mathrm{sn}^4u}\\\dn 2u&=\frac{1-2k^2\mathrm{sn}^2u+k^2\mathrm{sn}^4u}{1-k^2\mathrm{sn}^4u}\end{align}
定理30より$$\frac{1-\cn 2u}{2}=\frac{\mathrm{sn}^2u\:\mathrm{dn}^2u}{1-k^2\mathrm{sn}^4u}\;,\quad\frac{1+\dn 2u}{2}=\frac{\mathrm{dn}^2u}{1-k^2\mathrm{sn}^4u}$$辺辺割ると$$\mathrm{sn}^2u=\frac{1-\cn2u}{1+\dn2u}$$なる半角公式を得ます。これと、$$\mathrm{cn^2}u=1-\mathrm{sn}^2u\;,\quad\mathrm{dn^2}u=1-k^2\mathrm{sn}^2u$$を用いると、残り2つの半角公式も導けます。結果、
\begin{align}\mathrm{sn}^2u &= \frac{1-\cn2u}{1+\dn2u}\\\mathrm{cn}^2u &= \frac{\cn2u+\dn2u}{1+\dn2u}\\\mathrm{dn}^2u &= \frac{k'^{~2}+\dn2u+k^2\cn2u}{1+\dn2u}\end{align}
定理31と命題29から1/8周期($\dn u$ については1/4周期)の値を得ます。
$$\sn\frac{K}{2}=\frac{1}{\sqrt{1+k'}}\;,\;\;\cn\frac{K}{2}=\sqrt{\frac{k'}{1+k'}}\;,\;\; \dn\frac{K}{2}=\sqrt{k'}$$
命題23や命題24、そして微分を繰り返すことによりマクローリン展開を得ます。
\begin{align}\sn u &=u-\frac{1+k^2}{6}u^3+\frac{1+14k^2+k^4}{120}u^5-\cdots\\\cn u &= 1-\frac{1}{2}u^2+\frac{1+4k^2}{24}u^4-\cdots\\\dn u &=1-\frac{k^2}{2}u^2+\frac{k^2(4+k^2)}{24}u^4-\cdots\end{align}
Schett[4]には15次までの展開式があります。ネット無料で閲覧可。
純虚数への拡張
ヤコビの楕円関数が、三角関数や双曲線関数に似たものというならば、定義域を複素数に拡張してもその性質が保たれるのではないかと予想されます。
まず $\sn u$ の定義\begin{equation}u=\int_0^{\sn u}\frac{dt}{\sqrt{(1-t^2)(1-k^2t^2)}}\tag{2}\end{equation}で $u$ に $iu$ を代入すると\begin{equation}iu=\int_0^{\sn iu}\frac{dt}{\sqrt{(1-t^2)(1-k^2t^2)}}\tag{3}\end{equation}一方(2)で $x=\sn u$ とおくと$$u=\int_0^{x}\frac{dt}{\sqrt{(1-t^2)(1-k^2t^2)}}$$$x$ が純虚数の場合、$x=iy$ とおくと$$u=\int_0^{iy}\frac{dt}{\sqrt{(1-t^2)(1-k^2t^2)}}$$$t=is$ として$$u=i\int_0^{y}\frac{ds}{\sqrt{(1+s^2)(1+k^2s^2)}}$$$s=\tan\t$ として$$u=i\int_0^{\arctan y}\frac{d\t}{\sqrt{\cos^2\t+k^2\sin^2\t}}$$$$\therefore\quad iu=-\int_0^{\arctan y}\frac{d\t}{\sqrt{1-k'^2\sin^2\t}}$$$\sin\t=w$ と置換すると\begin{align}iu&=-\int_0^{\frac{y}{\sqrt{1+y^2}}}\frac{dw}{\sqrt{(1-w^2)(1-k'^{~2}w^2)}}\\&=\int_0^{\frac{-y}{\sqrt{1+y^2}}}\frac{dw}{\sqrt{(1-w^2)(1-k'^{~2}w^2)}}\\&=\int_0^{\frac{ix}{\sqrt{1-x^2}}}\frac{dw}{\sqrt{(1-w^2)(1-k'^{~2}w^2)}}\end{align}(3)と見比べることで$$\mathrm{sn}(iu,k')=\frac{ix}{\sqrt{1-x^2}}$$この $\sn$における母数は $k$ でなくて $k'$ であることを明示しています。$x=\sn u$ でしたから\begin{equation}\mathrm{sn}(iu,k')=i\frac{\mathrm{sn}(u,k)}{\mathrm{cn}(u,k)}\tag{4}\end{equation}右辺は $u\in\RR$ まで拡張済みですので、(4)は $\sn u$ の $u$ が純虚数の場合まで拡張できたことを示します。定理28より$$\frac{\mathrm{sn}(u+2K,k)}{\mathrm{cn}(u+2K,k)}=\frac{\mathrm{sn}(u,k)}{\mathrm{cn}(u,k)}$$ですから、(4)は周期 $2K$ を持ちます。
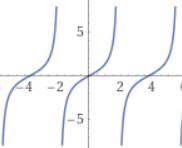
まるで $\tan u$ に瓜二つです。なお(4)のように、ヤコビの楕円関数の比が現れる場合、分子の頭文字と分母の頭文字を順にとって\begin{equation}\mathrm{sn}(iu,k')=i\:\mathrm{sc}(u,k)\tag{5}\end{equation}と書くこともあります。
残りの楕円関数は\begin{align}\cn u &:=\sqrt{1-\mathrm{sn}^2u}\tag{6a}\\\dn u &:=\sqrt{1-k^2\mathrm{sn}^2u}\tag{6b}\end{align}と(4)によって拡張します。なお(6a)(6b)において、複素数の範囲では根号は2価関数ですが、命題29と整合性がとれるように、$\cn 0=1$, $\dn0=1$ となるほうの値を選びます。\begin{align}\mathrm{cn}(iu,k')&=\sqrt{1-\mathrm{sn}^2(iu,k')}\\&=\sqrt{1+\frac{\mathrm{sn}^2(u,k)}{\mathrm{cn}^2(u,k)}}\\&=\frac{1}{\sqrt{\mathrm{cn}^2(u,k)}}\end{align}$u=0$ を代入したときに最左辺は $1$ ですから符号は+を選び\begin{equation}\mathrm{cn}(iu,k')=\frac{1}{\mathrm{cn}(u,k)}\tag{7}\end{equation}なお(7)のようにヤコビの楕円関数の逆数が現れる場合、その2文字を逆転して $\mathrm{nc}$ と書くこともあります。つまり\begin{equation}\mathrm{cn}(iu,k')=\mathrm{nc}(u,k)\tag{8}\end{equation}
最後に(6b)より\begin{align}\mathrm{dn}(iu,k')&=\sqrt{1-k'^2\mathrm{sn}^2(iu,k')}\\&=\sqrt{1+(1-k^2)\frac{\mathrm{sn}^2(u,k)}{\mathrm{cn}^2(u,k)}}\\&=\sqrt{\frac{\mathrm{dn}^2(u,k)}{\mathrm{cn}^2(u,k)}}\end{align}よって\begin{equation}\mathrm{dn}(iu,k')=\frac{\mathrm{dn}(u,k)}{\mathrm{cn}(u,k)}\tag{9}\end{equation}あるいは\begin{equation}\mathrm{dn}(iu,k')=\mathrm{dc}(u,k)\tag{10}\end{equation}とも書いてよいです。
結果をまとめると、$k'$ を $k$ とおきなおせば
\begin{align}\mathrm{sn}(iu,k)&=i\:\mathrm{sc}(u,k')\tag{a}\\\mathrm{cn}(iu,k)&=\mathrm{nc}(u,k')\tag{b}\\\mathrm{dn}(iu,k)&=\mathrm{dc}(u,k')\tag{c}\end{align}
簡単な値の確認
一応、定理34に簡単な母数を代入して確認しておきましょう。命題22から\begin{eqnarray*}\sn(u,0) &=& \sin u \quad ,\;\sn(u,1) =\tanh u\\\cn(u,0) &=& \cos u \quad ,\;\cn(u,1) =\mathrm{sech}\: u\\\dn(u,0) &=& \;\:1 \quad \quad,\;\dn(u,1) =\mathrm{sech}\: u\end{eqnarray*}であることに注意しておきます。
$k=0$ とすると、$k'=1$ なので定理34より\begin{align}\mathrm{sn}(iu,0)&=i\sinh u\tag{11a}\\\mathrm{cn}(iu,0)&=\cosh u\tag{11b}\\\mathrm{dn}(iu,0)&=1\tag{11c}\end{align}となりますが、これらの3式は、$$\mathrm{sn}(u,0)=\sin u\;,\quad\mathrm{cn}(u,0)=\cos u\;,\quad\mathrm{dn}(u,0)=1$$で $u$ に $iu$ を代入したものと一致しています。
また $k=1$ とすると定理34から\begin{align}\mathrm{sn}(iu,1)&=i\tan u\tag{12a}\\\mathrm{cn}(iu,1)&=\sec u\tag{12b}\\\mathrm{dn}(iu,1)&=\sec u\tag{12c}\end{align}と求まります。これらは$$\mathrm{sn}(u,1)=\tanh u\;,\quad\mathrm{cn}(u,1)=\mathrm{sech} u\;,\quad\mathrm{dn}(u,1)=\mathrm{sech} u$$で $u$ に $iu$ を代入したものと一致しています。
一般の複素数への拡張
前回記事の加法定理に定理34を用いることで、引数 $u+iv$ の関数形を導出できます。非常に簡単な計算なので結果のみ。簡単のため、$\mathrm{sn}(u,k)=\sn u$ , $\mathrm{sn}(u,k')=\mathrm{sn}'u$ のように、補母数のほうにダッシュを附すことにします(微分のダッシュではない!)。
\begin{align}\mathrm{sn}(u+iv) &= \frac{\sn u\:\mathrm{dn}'v+i\:\cn u\:\dn u\:\mathrm{sn}'v\:\mathrm{cn}'v}{\mathrm{cn}'^2v+k^2\mathrm{sn}^2u\:\mathrm{sn}'^2v}\\ \mathrm{cn}(u+iv) &= \frac{\cn u\:\mathrm{cn}'v-i\:\sn u\:\dn u\:\mathrm{sn}'v\:\mathrm{dn}'v}{\mathrm{cn}'^2v+k^2\mathrm{sn}^2u\:\mathrm{sn}'^2v}\\\mathrm{dn}(u+iv) &= \frac{\dn u\:\mathrm{cn}'v\:\mathrm{dn}'v-ik^2\sn u\:\cn u\:\mathrm{sn}'v}{\mathrm{cn}'^2v+k^2\mathrm{sn}^2u\:\mathrm{sn}'^2v}\end{align}
次回は、定理35で複素数に拡張されたヤコビの楕円関数についてもう少し深掘りしていきましょう。
楕円積分・楕円関数のことが平易に書かれています。

第5版です。いわずと知れた名著。ヤコビの楕円関数に1章を割いています。

楕円積分に関する定理がいろいろあります。興味深い式が多く導出されており、一見の価値あり。

Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。
