楕円関数の基礎を学習しましょう。楕円関数を学ぶたいていの場合、「二重周期をもつ関数」という一般論からスタートしますが、楕円積分の記事の続きとして構成するため、「ヤコビの楕円関数」という特別なものから導入します。ヤコビの楕円関数は、三角関数と類似の性質をもつので親しみやすいです。
前回の記事はこちら:
楕円積分がみたす微分方程式とルジャンドルの関係式・singular value
ここで学んだように第1種不完全楕円積分は\begin{eqnarray}F(x,k)&:=&\int_0^{x}\frac{dz}{\sqrt{(1-z^2)(1-k^2z^2)}}\tag{1a}\\F(\t\: ;k) &:=& \int_0^\t\frac{d\phi}{\sqrt{1-k^2\sin^2\phi}}\tag{1b}\end{eqnarray}ただし $0\le k<1$ としておきます。(1a)で $x=\sin\t$ としたものが(1b)であり、両者はほぼ同じものです。$$F(\t;k)=F(\sin\t,k)$$
あとで使う文字の便宜上、$F$ ではなく $u$ と書くことにして\begin{equation}u(x)=u(x,k):=\int_0^{x}\frac{dz}{\sqrt{(1-z^2)(1-k^2z^2)}}\tag{2}\end{equation}$k$ が固定されていることが多いので、引数 $k$ を省く場合があるよ、ということです。
$k=0$ の場合は$$u(x,0)=\int_0^{x}\frac{dz}{\sqrt{1-z^2}}$$\begin{equation}\therefore\quad u(x,0)=\arcsin x\tag{3}\end{equation}$k=1$ の場合は$$u(x,1)=\int_0^{x}\frac{dz}{1-z^2}$$\begin{equation}\therefore\quad u(x,1)=\frac{1}{2}\ln\frac{1+x}{1-x}=\mathrm{artanh}\:x\tag{4}\end{equation}となります。また(2)において $x=1$ とすれば第1種完全楕円積分となります。すなわち\begin{equation}u(1,k)=K(k)\tag{5}\end{equation}
これで準備は終わりました。では楕円関数の話に入りましょう。$-1\le x\le 1$ で定義される関数\begin{equation}u(x)=u(x,k):=\int_0^{x}\frac{dz}{\sqrt{(1-z^2)(1-k^2z^2)}}\tag{6}\end{equation}を考えます。$k$ を固定すると(2)は $x$ の関数 $u(x)$ の定義式となっています。これの逆関数 $x(u)$ を $\sn u$ と定義するのです。$k$ を明示するなら $\sn u=\sn(u,k)$ と書くことにします。(6)を踏まえて\begin{equation}u=\int_0^{\sn u}\frac{dz}{\sqrt{(1-z^2)(1-k^2z^2)}}\;,\quad -1\le \sn u\le 1\tag{7}\end{equation}とできます。
何やら得体のしれない感じがします。そこでとりあえず(6)をプロットすると
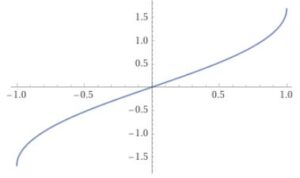
(5)より $u(1)=K$ , $u(-1)=-K$ であることに注意します($K(k)$ の引数 $k$ は省略している!)。グラフでは $k=1/2$ としていますので、$K\approx1.69$ です。この逆関数が $\sn u$ なので、$y=x$ に関して対称にひっくり返せば $\sn u$ のグラフとなります。
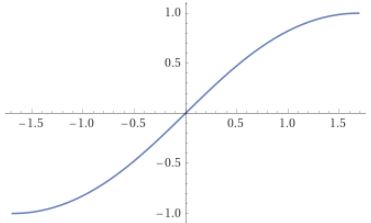
したがって(7)は、母数 $k$ に応じて定まる"定数" $K$ を用いて\begin{equation}u=\int_0^{\sn u}\frac{dz}{\sqrt{(1-z^2)(1-k^2z^2)}}\;,\quad -K\le u\le K\tag{8}\end{equation}$K$ は本来第1種完全楕円積分($k$ の関数)ですが、$k$ が定まれば定数と見てよいです。$K(k)$ の定義より明らかに\begin{equation}K(0)=\frac{\pi}{2}\quad,\quad K(1)=+\infty\tag{9}\end{equation}です。
図(2)を見ると、$\sn u$ は $\sin u$ と似ていることが分かります。実際(3)で $x=\sn u$ より\begin{equation}\sn(u,0)=\sin u\quad(u\in[-\frac{\pi}{2},\frac{\pi}{2}])\tag{10}\end{equation}ついでに(4)でも同様に\begin{equation}\sn(u,1)=\tanh u\quad(u\in\RR)\tag{11}\end{equation}いま図(2)や式(8)では定義域が($\sin$ でいうところの)半周期分になっていますが、これを延長して波がずっと続くように定義域は拡張されます。この拡張は、のちに加法定理の話をするときに正当化する予定です。
$$\sn\bigl(F(\t\:;k),k\bigr)=\sin\t$$および$$F\bigl(\arcsin(\sn(u,k))\:;k\bigr)=u$$を示せ。
$u(\sin\t,k)=F(\t\:; k)$となることを用いれば直ちに従います。
ここではほぼ使いませんが、$F(\t;k)$ の $\t$ に関する逆関数を振幅関数 $\mathrm{am}(u,k)$ と定義します。つまり$$u(\t,k):= \int_0^\t\frac{d\phi}{\sqrt{1-k^2\sin^2\phi}}$$と $u$ を定めて$$\mathrm{am}(u,k)=\t\;,\quad F\bigl(\mathrm{am}(u,k),k)=u$$また第1種完全楕円積分の定義から$$\mathrm{am} K=\frac{\pi}{2}$$
$\sn$ と合わせて合計3つの関数を次のように定義します。
$u\in[-K,K]$ ,\begin{eqnarray}u&=&\int_0^{\sn(u,k)}\frac{dt}{\sqrt{(1-t^2)(1-k^2t^2)}}\tag{12a}\\u&=&\int_{\cn(u,k)}^1\frac{dt}{\sqrt{(1-t^2)(k'^2+k^2t^2)}}\tag{12b}\\u&=&\int_{\dn(u,k)}^1\frac{dt}{\sqrt{(1-t^2)(t^2-k'^2)}}\tag{12c}\end{eqnarray}
つまりそれぞれ\begin{eqnarray}u(x)&=&\int_0^x\frac{dt}{\sqrt{(1-t^2)(1-k^2t^2)}}\tag{13a}\\u(x)&=&\int_x^1\frac{dt}{\sqrt{(1-t^2)(k'^2+k^2t^2)}}\tag{13b}\\u(x)&=&\int_x^1\frac{dt}{\sqrt{(1-t^2)(t^2-k'^2)}}\tag{13c}\end{eqnarray}の逆関数というわけです。この$\sn,\cn,\dn$ をまとめてヤコビの楕円関数とよびます。読み方は知りませんが、私は心の中で $\sn u$, $\cn u$, $\dn u$ を「スンユー、クンユー、ドゥンユー」と発音しています。
ヤコビの楕円関数を、テータ関数によって定義することもあります。本記事ではテータ関数は未習という前提なので、別のアプローチをとります。
(12a)で $s=\sqrt{1-t^2}$ と置換すると$$u=\int_{\sqrt{1-\mathrm{sn}^2(u,k)}}^1\frac{ds}{\sqrt{(1-s^2)(k'^2+k^2s^2)}}$$また、(12a)で $s=\sqrt{1-k^2t^2}$ と置換すると$$u=\int_{\sqrt{1-k^2\mathrm{sn}^2(u,k)}}^1\frac{ds}{\sqrt{(1-s^2)(s^2-k'^2)}}$$したがって
\begin{eqnarray}\mathrm{sn}^2u+\mathrm{cn}^2u&=&1\tag{14a}\\k^2\mathrm{sn}^2u+\mathrm{dn}^2u&=&1\tag{14b}\end{eqnarray}
なる関係があります。なお、定義19の定義域および導出の過程から分かるように、$-K\le u\le K$ においては $\cn u\ge0$ , $\dn u\ge 0$ です。なので $\sn u$ から定理20を使って $\cn u,\dn u$ を求める場合、それらの符号は正として定まるわけです。\begin{equation}\cn u=\sqrt{1-\sn^2u}\;,\quad \dn u=\sqrt{1-k^2\sn^2u}\tag{14c}\end{equation}$\sn u$ が奇関数であるのに対し、これら2つは偶関数となっています。(14c)を $\cn u$, $\dn u$ の定義として採用してもよいです。
$k$ を固定します。$\sn 0=0$ , $\sn(\pm K)=\pm 1$ を思い出せば定理20より
\begin{eqnarray*}\sn(0) &=& 0 \quad ,\sn(\pm K) =\pm 1\\\cn(0) &=& 1 \quad ,\cn(\pm K) =0\\\dn(0) &=& 1 \quad ,\dn(\pm K) =k'\end{eqnarray*}1行目は複号同順である。
一方 $k$ への依存性としては、(10)(11)と定理20により
\begin{eqnarray*}\sn(u,0) &=& \sin u \quad ,\;\sn(u,1) =\tanh u\\\cn(u,0) &=& \cos u \quad ,\;\cn(u,1) =\mathrm{sech}\: u\\\dn(u,0) &=& \;\:1 \quad \quad,\;\dn(u,1) =\mathrm{sech}\: u\end{eqnarray*}定義域は(9)参照。
特に $k=0$ ではサイン・コサインが現れています。そういう意味では、ヤコビの楕円関数は三角関数の一般化の1つといえそうです。
新しい関数を導入したのですから、その微分を試みるのは自然なことでしょう。
(12a)を $u$ で微分すると\begin{eqnarray*}1&=&\frac{1}{\sqrt{(1-\mathrm{sn}^2u)(1-k^2\mathrm{sn}^2u)}}\frac{d\:\sn u}{du}\\&=&\frac{1}{\sn u\dn u}\frac{d\:\sn u}{du}\end{eqnarray*}(12b)を $u$ で微分すると\begin{eqnarray*}1 &=&\frac{-1}{\sqrt{(1-\mathrm{cn}^2u)(1-k^2+k^2\mathrm{cn}^2u)}}\frac{d\:\cn u}{du}\\&=& \frac{-1}{\sn u\dn u}\frac{d\:\cn u}{du}\end{eqnarray*}これらから $\sn'u$ と $\cn'u$ が求まります。そして(14b)を微分すれば $\dn'u$ も求まります。結果は
\begin{eqnarray*}\frac{d\:\sn u}{du}&=&\cn u\:\dn u\\\frac{d\:\cn u}{du}&=&-\sn u\:\dn u\\\frac{d\:\dn u}{du}&=&-k^2\sn u\:\cn u\end{eqnarray*}
$k=0$ としたとき、命題22と合わせると単なる三角関数の微分公式であることが分かります。
命題23を再度微分したくなってきますね。(14a)(14b)も用いてうまく変形しながらやってみると
\begin{eqnarray*}\frac{d^2\sn u}{du^2}&=&2k^2\mathrm{sn}^3u-(1+k^2)\sn u\\\frac{d^2\cn u}{du^2}&=&-2k^2\mathrm{cn}^3u+(2k^2-1)\cn u\\\frac{d^2\dn u}{du^2}&=&-2\mathrm{dn}^3u+(2-k^2)\dn u\end{eqnarray*}
ちょっとした計算練習になるので、ぜひ確かめてみてください。
$$\int_0^K \mathrm{dn}^2u du=E$$を示せ。$\sin\t=\sn u$ の置換をするとよい。
命題24はそもそも3つの楕円関数が満たす2階非線型微分方程式の形になっています。例えば1行目なら$$y''+(1+k^2)y-2k^2y^3=0$$これに $y'$ をかけて積分する、または命題23の1行目を2乗することにより$$(y')^2=(1-y^2)(1-k^2y^2)$$もまた $\sn u$ を解とする微分方程式です。まとめると
$y=\sn u$ を解に持つ方程式は\begin{eqnarray*}y''+(1+k^2)y-2k^2y^3=0\\(y')^2=(1-y^2)(1-k^2y^2)\end{eqnarray*}$y=\cn u$ を解に持つ方程式は\begin{eqnarray*}y''+(1-2k^2)y+2k^2y^3=0\\(y')^2=(1-y^2)(k'^2+k^2y^2)\end{eqnarray*}$y=\dn u$ を解に持つ方程式は\begin{eqnarray*}y''-(2-k^2)y+2y^3=0\\(y')^2=(1-y^2)(y^2-k'^2)\end{eqnarray*}
それぞれの2行目の方程式は、定義19の被積分関数の形に由来することが分かります。
$\sn u$ は $k$ の値によって多少の形は変わるものの、命題22より三角関数あるいは双曲線関数の親戚のような感があります。なのでヤコビの楕円関数にも加法定理のようなものがあるのではないかと考えられます。
$u+v$ を定数 $\a$ とすると\begin{equation}\dot{v}=-1\tag{15}\end{equation}ただし本記事では $u$ による微分をドットで表現しています。簡単のため $s_1:=\sn u$ , $s_2:=\sn v=\sn(\a-u)$ とおきます。定理25と(15)から\begin{eqnarray}\dot{s_1}^2 &=& (1-s_1^{~2})(1-k^2s_1^{~2})\tag{16a}\\\dot{s_2}^2 &=& (1-s_2^{~2})(1-k^2s_2^{~2})\tag{16b}\\\ddot{s_1} &=& -(1+k^2)s_1+2k^2s_1^{~3}\tag{16c}\\\ddot{s_2} &=& -(1+k^2)s_2+2k^2s_2^{~3}\tag{16d}\end{eqnarray}この4つを使って次の式を作れます:$$\frac{\ddot{s_1}s_2-\ddot{s_2}s_1}{\dot{s_1}^2s_2^{~2}-\dot{s_2}^2s_1^{~2}}=\frac{-2k^2s_1s_2}{1-k^2s_1^{~2}s_2^{~2}}$$↑は左辺の分母・分子を別々にやってから約分すると簡単に得られます。で、これを少し変形すると$$\frac{\ddot{s_1}s_2-\ddot{s_2}s_1}{\dot{s_1}s_2-\dot{s_2}s_1}=\frac{-2k^2s_1s_2(\dot{s_1}s_2+\dot{s_2}s_1)}{1-k^2s_1^{~2}s_2^{~2}}$$なかなか気づかないですが、左辺の分子と右辺の分子は次のように書き改められます。$$\frac{\frac{d}{du}(\dot{s_1}s_2-\dot{s_2}s_1)}{\dot{s_1}s_2-\dot{s_2}s_1}=\frac{\frac{d}{du}(1-k^2s_1^{~2}s_2^{~2})}{1-k^2s_1^{~2}s_2^{~2}}$$$u$ で積分すると対数となり、$$\frac{\dot{s_1}s_2-\dot{s_2}s_1}{1-k^2s_1^{~2}s_2^{~2}}=C$$$C$ は定数です。
さて、これを定義に戻って書き直すと$$\frac{\dot{\mathrm{sn}}u\:\sn v-\dot{\mathrm{sn}}v\:\sn u}{1-k^2\mathrm{sn}^2u\:\mathrm{sn}^2v}=C$$命題23より $\sn$ の微分は分かっているので、(15)に注意しつつ$$\frac{\cn u\:\dn u\:\sn v+\cn v\:\dn v\:\sn u}{1-k^2\mathrm{sn}^2u\:\mathrm{sn}^2v}=C$$$u=0$ とおくと $v=\a$ なので $C=\sn\a$ となります。すなわち$$\sn\a=\frac{\cn u\:\dn u\:\sn(\a-u)+\cn(\a-u)\:\dn(\a-u)\:\sn u}{1-k^2\mathrm{sn}^2u\:\mathrm{sn}^2(\a-u)}$$再度 $\a=u+v$ として加法定理を得ます:\begin{equation}\mathrm{sn}(u+v)=\frac{\sn u\:\cn v\:\dn v+\sn v\:\cn u\:\dn u}{1-k^2\mathrm{sn}^2u\:\mathrm{sn}^2v}\tag{17}\end{equation}(17)と定理20から $\cn$ と $\dn$ の加法定理も得られます。\begin{eqnarray*}(1-k^2\mathrm{sn}^2u\mathrm{sn}^2v)\mathrm{cn}^2(u+v) &=& (1-k^2\mathrm{sn}^2u\mathrm{sn}^2v)(1-\mathrm{sn}^2(u+v))\\&=& 1-2k^2\mathrm{sn}^2u\mathrm{sn}^2v+k^4\mathrm{sn}^4u\mathrm{sn}^4v-2\mathrm{sn} u\mathrm{sn} v\mathrm{cn} u\mathrm{cn} v\mathrm{dn} u \mathrm{dn} v\\&&\quad-\sn^2u\cn^2v\dn^2v-\sn^2v\cn^2u\dn^2u\\&=&1-2k^2\mathrm{sn}^2u\mathrm{sn}^2v+k^4\mathrm{sn}^4u\mathrm{sn}^4v-2\mathrm{sn} u\mathrm{sn} v\mathrm{cn} u\mathrm{cn} v\mathrm{dn} u \mathrm{dn} v\\&&\quad-\mathrm{sn}^2u(1-\mathrm{sn}^2v)(1-k^2\mathrm{sn}^2v)-\mathrm{sn}^2v(1-\mathrm{sn}^2u)(1-k^2\mathrm{sn}^2u)\end{eqnarray*}最終行は全部展開します。\begin{eqnarray*} &=& 1+k^4\mathrm{sn}^4u\mathrm{sn}^4v-2\mathrm{sn} u\mathrm{sn} v\mathrm{cn} u\mathrm{cn} v\mathrm{dn} u \mathrm{dn} v\\&&\quad-\mathrm{sn}^2u(1-\mathrm{sn}^2v+k^2\sn^2u\sn^2v)-\mathrm{sn}^2v(1-\mathrm{sn}^2u+k^2\sn^2u\sn^2v)\\&=&(1-\mathrm{sn}^2u)(1-\mathrm{sn}^2v)+k^4\mathrm{sn}^4u\mathrm{sn}^4v-2\mathrm{sn} u\mathrm{sn} v\mathrm{cn} u\mathrm{cn} v\mathrm{dn} u \mathrm{dn} v\\&&\quad-k^2\mathrm{sn}^4u\mathrm{sn}^2v-k^2\mathrm{sn}^2u\mathrm{sn}^4v+\mathrm{sn}^2u\mathrm{sn}^2v\\&=&\mathrm{cn}^2u\mathrm{cn}^2v-2\mathrm{sn} u\mathrm{sn} v\mathrm{cn} u\mathrm{cn} v\mathrm{dn} u \mathrm{dn} v\\&&\quad +\mathrm{sn}^2u\mathrm{sn}^2v(1-k^2\mathrm{sn}^2u)(1-k^2\mathrm{sn}^2v)\\&=&\mathrm{cn}^2u\mathrm{cn}^2v-2\mathrm{sn} u\mathrm{sn} v\mathrm{cn} u\mathrm{cn} v\mathrm{dn} u \mathrm{dn} v +\mathrm{sn}^2u\mathrm{sn}^2v\mathrm{dn}^2u\mathrm{dn}^2v\\&=&(\cn u\:\cn v-\sn u\:\sn v\:\dn u\:\dn v)^2\end{eqnarray*}二乗を外すときは $v=0$ とするなどして正しい符号をとります。以上から\begin{equation}\mathrm{cn}(u+v)=\frac{\cn u\:\cn v-\sn u\:\sn v\:\dn u\:\dn v}{1-k^2\mathrm{sn}^2u\:\mathrm{sn}^2v}\tag{18}\end{equation}$\dn$ も同様にして加法定理が得られます。\begin{equation}\mathrm{dn}(u+v)=\frac{\dn u\:\dn v-k^2\sn u\:\sn v\:\cn u\:\cn v}{1-k^2\mathrm{sn}^2u\:\mathrm{sn}^2v}\tag{19}\end{equation}
次回は:
ヤコビの楕円関数2(定義域の拡張・半角公式・倍角公式・展開)
楕円積分・楕円関数のことが平易に書かれています。本記事の構成は本書に沿っています。

第5版です。いわずと知れた名著。ヤコビの楕円関数に1章を割いています。

楕円積分に関する定理がいろいろあります。興味深い式が多く導出されており、一見の価値あり。

Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。

