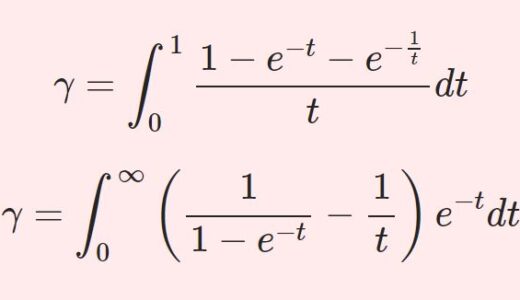「ガンマ関数の基礎」シリーズ第13回です。前回は:
$$\G(z)=\frac{2a^ze^a}{\sin\pi z}\int_0^\infty e^{-ax^2}(1+x^2)^{z-\frac{1}{2}}\cos[2ax+(2z-1)\arctan x]dx$$
Whittaker-Watsonのガンマ関数の例題に載っていた表示です。何に使えるのかは分かりませんが、導出すること自体は面白そうなので取り組んでみました。
古いですが有名な書物で、どんどん改訂版が出ています。前半は解析学一般、後半は特殊関数という内容で、網羅的に勉強できます。演習問題に解答がないのが昔ながらのものって感じ。2022/11/6現在、最新版は5th Editionで私も所有していますが、廉価な3rdとかでも十分かと。

A Course of Modern Analysis: fifth Edition

A Course of Modern Analysis: Third Edition
しかし自力ではなかなか導き出すことができませんでした。そこでこの公式が最初に出てきた原論文に当たりました。それは「Acta Mathematica」という雑誌の第1巻(1882年)。Bourguet(ブルゲ)という人が書いた"Sur quelques intégrales définies"と題する論文です。

フランス語?なので全然読めませんが、数式を追うだけなら何とかなります。積分路をどうするかが分かれば、あとは加法定理だとか和積の公式だとか、三角関数の計算練習みたいなものです。
スタートとなるのは過去記事でも紹介した「ハンケルの積分表示」です。
\begin{equation}\G(z)=-\frac{1}{2i\sin\pi z}\int_C e^{-t}(-t)^{z-1}dt\quad(z\notin\ZZ)\tag{1}\end{equation}

経路 $C$ を簡単に説明します。$t=re^{i\t}$ $(0<\t<2\pi)$ とすると、まず $r=\infty, \theta=+0$ から原点へやってきて、原点を1周して最後は $r=\infty,\t=2\pi-0$ となるような曲線です。これを満たしていれば形が変化してもよく、例えば(1)を導出する際には下のような経路を使いました。

このあたりの話については下の記事を参照:
この事実を使ってブルゲの表示を導きましょう。
積分路の設定
(1)の積分において$$-t=2a\frac{\cos\t+i\sin\t}{1+\cos\t}\quad(-\pi<\t<\pi)$$とします。$t$ ではなく $-t$ で置いていることに注意してください。偏角 $\t$ を変化させると下図のような放物線を描きます($-t$ の複素平面)。

$x=\dfrac{2a\cos\t}{1+\cos\t}$ , $y=\dfrac{2a\sin\t}{1+\cos\t}$ とおくと$$\cos\t=\frac{\frac{x}{2a}}{1-\frac{x}{2a}}\;,\;\sin\t=\frac{\frac{y}{2a}}{1-\frac{x}{2a}}$$2乗して辺々足すと$1$であることから$$4a^2-4ax=y^2$$となり、原点を焦点とする放物線であることが分かる。
値の計算
微小要素は$$dt=2a\frac{\sin\t-i(1+\cos\t)}{(1+\cos\t)^2}d\t$$よってゴリゴリ計算していくと\begin{eqnarray*}&&\int_C e^{-t}(-t)^{z-1}dt\\&=&\int_{-\pi}^\pi\left(2a\frac{\cos\t+i\sin\t}{1+\cos\t}\right)^{z-1}e^{2a\frac{\cos\t+i\sin\t}{1+\cos\t}}2a\frac{\sin\t-i(1+\cos\t)}{(1+\cos\t)^2}d\t\\&=&2^za^z\int_{-\pi}^\pi\frac{(\cos\t+i\sin\t)^{z-1}}{(1+\cos\t)^{z+1}}e^{2a\frac{\cos\t+i\sin\t}{1+\cos\t}}[\sin\t-i(1+\cos\t)]d\t\\&=&2^za^z\int_{-\pi}^\pi\frac{[\cos(z-1)\t+i\sin(z-1)\t][\sin\t-i(1+\cos\t)]}{(1+\cos\t)^{z+1}}e^{2a\frac{\cos\t+i\sin\t}{1+\cos\t}}d\t\\&=&2^za^z\int_{-\pi}^\pi\frac{\sin z\t+\sin(z-1)\t-i(\cos z\t+\cos(z-1)\t)}{(1+\cos\t)^{z+1}}e^{2a\frac{\cos\t+i\sin\t}{1+\cos\t}}d\t\\&=&2^za^z\int_{-\pi}^\pi\frac{2\sin\frac{2z-1}{2}\t\cos\frac{\t}{2}-2i\cos\frac{2z-1}{2}\t\cos\frac{\t}{2}}{2^{z+1}\cos^{2z+2}\frac{\t}{2}}e^{2a\frac{\cos\t+i\sin\t}{1+\cos\t}}d\t\\&=&a^z\int_{-\pi}^\pi\frac{\sin\frac{2z-1}{2}\t-i\cos\frac{2z-1}{2}\t}{\cos^{2z+1}\frac{\t}{2}}e^{2a\frac{\cos\t+i\sin\t}{1+\cos\t}}d\t\\&=&a^z\int_{-\pi}^\pi\frac{\sin\frac{2z-1}{2}\t-i\cos\frac{2z-1}{2}\t}{\cos^{2z+1}\frac{\t}{2}}e^{2a(1-\frac{1}{1+\cos\t}+\frac{i\sin\t}{1+\cos\t})}d\t\\&=&a^ze^a\int_{-\pi}^\pi\frac{\sin\frac{2z-1}{2}\t-i\cos\frac{2z-1}{2}\t}{\cos^{2z+1}\frac{\t}{2}}e^{-a\tan^2\frac{\t}{2}}e^{i2a\tan\frac{\t}{2}}d\t\\&=&a^ze^a\int_{-\pi}^\pi\frac{(\sin\frac{2z-1}{2}\t-i\cos\frac{2z-1}{2}\t)(\cos2a\tan\frac{\t}{2}+i\sin2a\tan\frac{\t}{2})}{\cos^{2z+1}\frac{\t}{2}}e^{-a\tan^2\frac{\t}{2}}d\t\\&=&a^ze^a\int_{-\pi}^\pi\frac{\sin(\frac{2z-1}{2}\t+2a\tan\frac{\t}{2})-i\cos(\frac{2z-1}{2}\t+2a\tan\frac{\t}{2})}{\cos^{2z+1}\frac{\t}{2}}e^{-a\tan^2\frac{\t}{2}}d\t\end{eqnarray*}分子第1項は奇関数、分子第2項は偶関数なので$$=-2ia^ze^a\int_0^\pi\frac{\cos(\frac{2z-1}{2}\t+2a\tan\frac{\t}{2})}{\cos^{2z+1}\frac{\t}{2}}e^{-a\tan^2\frac{\t}{2}}d\t$$$x=\tan\frac{\t}{2}$ とおくと $d\t=2\cos^2\frac{\t}{2}dx$ ですから$$=-4ia^ze^a\int_0^\infty\cos[(2z-1)\arctan x+2ax](1+x^2)^{z-\frac{1}{2}}e^{-ax^2}dx$$これと$$\G(z)=-\frac{1}{2i\sin\pi z}\int_C e^{-t}(-t)^{z-1}dt$$を合わせることで結論を得ます。
\begin{equation}\G(z)=\frac{2a^ze^a}{\sin\pi z}\int_0^\infty e^{-ax^2}(1+x^2)^{z-\frac{1}{2}}\cos[2ax+(2z-1)\arctan x]dx\tag{2}\end{equation}
冒頭で紹介したブルゲの論文では $a=1/2$ としたときの同じ表示を導出していますので、ここで示した公式はその一般化といえます。三角関数の計算がごちゃごちゃしましたが、たどり着くと達成感があるものです。
$$\int_0^\infty\frac{e^{-x^2}\cos(2x-4\arctan x)}{(1+x^2)^2}dx=\frac{2\sqrt{\pi}}{3e}$$
(2)で $a=1$ , $z=-3/2$ とすると導出できます。Wolframで計算すると両辺ともに約0.4347で一致しています。
ここ数回でガンマ関数や対数ガンマ関数の積分表示を見てきました。次回からはディガンマ関数の積分表示をガンガン導出していきましょう!
次回:
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。