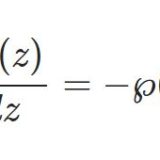前4回はこちら:
ワイエルシュトラスのペー関数の話の続きです。$$\O_{m,n}:=m\o_1+n\o_2$$とおくとワイエルシュトラスのペー関数は\begin{equation}\wp(z):=\frac{1}{z^2}+\sum_{m,n}'\left[\frac{1}{(z-\O_{m,n})^2}-\frac{1}{\O_{m,n}^{~2}}\right]\tag{0a}\end{equation}と定義されます。ここで $\sum'$ は $m,n$ がともにゼロとなる場合を除き全整数にわたって和をとるものです。またよくあらわれる等式として\begin{equation}\wp'(z)^2-4\wp(z)^3+g_2\wp(z)+g_3=0\tag{0b}\end{equation}さらに楕円積分の逆関数としても表せます:\begin{equation}z=\int_{\wp(z)}^\infty(4t^3-g_2t-g_3)^{-\frac{1}{2}}dt\tag{0c}\end{equation}
もくじ
周期 $\o_1,\o_2$ に対して $\o_1+\o_2+\o_3=0$ となる $\o_3$ を定義しておきます。
前回導出したことを再掲します。
ペー関数 $\wp(z)$ の導関数の零点における値を$$\wp\left(\frac{\o_1}{2}\right):=e_1\;,\quad\wp\left(\frac{\o_2}{2}\right):=e_2\;,\quad\wp\left(\frac{\o_3}{2}\right):=e_3$$とおくと $e_1$,$e_2$,$e_3$ は互いに異なり、3次方程式$$4t^3-g_2t-g_3=0$$の3解となる。そのため解と係数の関係\begin{align}e_1+e_2+e_3 &=0\\e_1e_2+e_2e_3+e_3e_1&=-\frac{g_2}{4}\\e_1e_2e_3&=\frac{g_3}{4}\end{align}を満たす。
$g_2,g_3\in\RR$ のとき$$g_2^{~3}-27g_3^{~2}>0$$であれば、定理1の $e_1,e_2,e_3$ は相異なる実数である。
なお $\Delta :=g_2^{~3}-27g_3^{~2}$ をモジュラー判別式とよぶ。
$g_2,g_3\in\RR$ かつ $e_1,e_2,e_3\in\RR$ とする。$e_1>e_2>e_3$ と定めれば\begin{align}\frac{\o_1}{2}&=\int_{e_1}^{+\infty}(4t^3-g_2t-g_3)^{-\frac{1}{2}}dt\\\frac{\o_3}{2}&=-i\int_{-\infty}^{e_3}(-4t^3+g_2t+g_3)^{-\frac{1}{2}}dt\end{align}として周期が求まる。
ペー関数を定義するときには、2つの周期 $\o_1,\o_2$ から決定する場合と2つの不変量 $g_2,g_3$ から決定する場合があるのでした。ということは $\o_1,\o_2$ から $g_2,g_3$ が求まるであろうし、その逆もしかりです。
今回は、定理3によって不変量から周期を求めてみようと思います。
$\wp(z)$ のパラメータとして周期や不変量を明示する場合には$$\wp\left(z\left|\begin{matrix}\o_1\\\o_2\end{matrix}\right.\right)$$とか$$\wp(z;g_2,g_3)$$のように書きます。
ペー関数の周期 $\o_1,\o_2$ が決まっていれば不変量も決まります。\begin{align}g_2(\o_1,\o_2)&=60G_4(\o_1,\o_2)=60\sum_{m,n}'\frac{1}{(m\o_1+n\o_2)^4}\tag{0d}\\ g_3(\o_1,\o_2)&=140G_6(\o_1,\o_2)=140\sum_{m,n}'\frac{1}{(m\o_1+n\o_2)^6}\tag{0e}\end{align}のように書くことができます。$G_k$ をアイゼンシュタイン級数というのでした。
逆に $g_2,g_3$ が決まっているとき $\o_1,\o_2$ は求まるのでしょうか。実際に求める方法を特殊なケースに限り後述するものの、一般には難しいです。ここまでの話をふまえて言えることを述べておきます。
$g_2,g_3$ はそもそもペー関数を級数展開したときの、それぞれ2次、4次の係数として現れるのでした。6次以降の係数もすべて $g_2,g_3$ で表すことができるので $g_2,g_3$ はペー関数をただ1つに決定します。
ではそのように決まった $\wp(z;g_2,g_3)$ に対応する周期 $\o_1,\o_2$ は求まるのか。つまり$$\wp(z;g_2,g_3)=\wp\left(z\left|\begin{matrix}\o_1\\\o_2\end{matrix}\right.\right)$$となる $\o_1,\o_2$ は求まるのか?ということです。それは定理3を使えば(もし計算ができるなら)可能です。
ただし気をつけるべきは、周期の取り方は1通りではないということです。ペー関数の定義(0a)あるいは不変量の定義(0d)(0e)から分かるように、例えば $\o_1$ を $-\o_1$ としてもペー関数は変わりません。また $\o_2$ を $\o_3$ に変えても不変です。$0$,$\o_1$,$\o_1+\o_2$,$\o_2$ でつくられる平行四辺形を単位格子とよびます。この格子の頂点を複素平面にたくさん描きだしてみます。すると $0$,$\o_1$,$\o_1+\o_3$,$\o_3$(ただし $\o_3=-\o_1-\o_2$)なる平行四辺形も単位格子となっています。この新しい単位格子はちゃんと全平面を埋め尽くし、もとの格子の頂点をすべて頂点としてもちます。つまり$$\wp\left(z\left|\begin{matrix}\o_1\\\o_2\end{matrix}\right.\right)=\wp\left(z\left|\begin{matrix}-\o_1\\\o_2\end{matrix}\right.\right)=\wp\left(z\left|\begin{matrix}\o_1\\\o_3\end{matrix}\right.\right)$$ということがとりあえず分かります。
より一般に$$\begin{pmatrix}\o_1'\\\o_2'\end{pmatrix}=\begin{pmatrix}a & b\\c & d\end{pmatrix}\begin{pmatrix}\o_1\\\o_2\end{pmatrix}\quad a,b,c,d\in\ZZ$$なる変換で\begin{equation}\begin{vmatrix}a & b\\c & d\end{vmatrix}=\pm 1\tag{0f}\end{equation}を満たす場合$$\wp\left(z\left|\begin{matrix}\o_1'\\\o_2'\end{matrix}\right.\right)=\wp\left(z\left|\begin{matrix}\o_1\\\o_2\end{matrix}\right.\right)$$となります[2]。
不変量が $g_2=1$ , $g_3=0$ のときを考えます。このとき定理1の3次方程式は\begin{equation}4t^3-t=0\tag{1}\end{equation}であり、解は $t=0$ , $\pm 1/2$ です。定理3に合わせて\begin{equation}e_1=\frac{1}{2}\;,\quad e_2=0\;,\quad e_3=-\frac{1}{2}\tag{2}\end{equation}とおきます。
周期の計算
定理3より\begin{equation}\frac{\o_1}{2}=\int_{\frac{1}{2}}^{+\infty}(4t^3-t)^{-\frac{1}{2}}dt\tag{3}\end{equation}$2t=u$ と置換して$$=\frac{1}{\sqrt{2}}\int_1^{+\infty}\frac{du}{\sqrt{u^3-u}}$$$u=1/y$ と置換して$$=\frac{1}{\sqrt{2}}\int_0^1\frac{dy}{\sqrt{y(1-y^2)}}$$ベータ関数が現れそうです。それを目指して $y^2=x$ と置換しましょう。$$=\frac{1}{2\sqrt{2}}\int_0^1 x^{-\frac{3}{4}}(1-x)^{-\frac{1}{2}}dx$$ベータ関数の定義およびガンマ関数との関係から$$=\frac{1}{2\sqrt{2}}\frac{\sqrt{\pi}\G(\frac{1}{4})}{\G(\frac{3}{4})}$$相反公式により\begin{equation}\o_1=\frac{\G(\frac{1}{4})^2}{2\sqrt{\pi}}\tag{4}\end{equation}
次に\begin{equation}\frac{\o_3}{2}=-i\int_{-\infty}^{-\frac{1}{2}}(-4t^3+t)^{-\frac{1}{2}}dt\tag{5}\end{equation}では $2t=-u$ と置換すればあとは同様の計算で\begin{equation}\o_3=-i\frac{\G(\frac{1}{4})^2}{2\sqrt{\pi}}\tag{6}\end{equation}これに対応するペー関数の2つの周期 $(\o_1,\o_2)$ を(4)(6)として構いませんので
$g_2=1$ , $g_3=0$ のとき、対応するペー関数の周期は\begin{equation}\begin{pmatrix}\o_1\\\o_2\end{pmatrix}=\frac{\G\left(\frac{1}{4}\right)^2}{2\sqrt{\pi}}\begin{pmatrix}1\\i\end{pmatrix}\tag{7}\end{equation}
となります。ただし(6)の負号は外しました。
アイゼンシュタイン級数の値
(7)より、逆にこの周期が与えられれば不変量が定まるので次のように書けます。\begin{align}g_2\left(\frac{\G\left(\frac{1}{4}\right)^2}{2\sqrt{\pi}},i\frac{\G\left(\frac{1}{4}\right)^2}{2\sqrt{\pi}}\right)&=1\tag{8a}\\ g_3\left(\frac{\G\left(\frac{1}{4}\right)^2}{2\sqrt{\pi}},i\frac{\G\left(\frac{1}{4}\right)^2}{2\sqrt{\pi}}\right)&=0\tag{8b}\end{align}(0d)(0e)より\begin{align}g_2(\lambda\o_1,\lambda\o_2) &=\lambda^{-4}g_2(\o_1,\o_2)\tag{9a}\\g_3(\lambda\o_1,\lambda\o_2) &=\lambda^{-6}g_2(\o_1,\o_2)\tag{9b}\end{align}であり、$\lambda=\frac{\G\left(\frac{1}{4}\right)^2}{2\sqrt{\pi}}$ とおけば
\begin{equation}g_2(1,i)=\frac{\G(\frac{1}{4})^8}{16\pi^2}\;,\quad g_3(1,i)=0\tag{10}\end{equation}
これと(0d)(0e)からアイゼンシュタイン級数 $G_4$ , $G_6$ も求まります。$G_8,G_{10},\cdots$ も $G_4$ , $G_6$ で表せるのでした。詳細は\begin{align}G_4 &=\frac{1}{60}g_2\\G_6 &=\frac{1}{140}g_3\\G_8 &=\frac{3}{7}G_4^{~2}\\G_{10} &=\frac{15}{11}G_4G_6\\G_{12}&=\frac{18}{143}G_4^{~3}+\frac{25}{143}G_6^{~2}\\G_{14}&=\frac{30}{143}G_4^{~2}G_6\\&\vdots\end{align}のようになります。以上をまとめると
$\wp(z)$ の周期が $1$ , $i$ のとき、不変量は$$g_2(1,i)=\frac{\G(\frac{1}{4})^8}{16\pi^2}\;,\quad g_3(1,i)=0$$あらわれるアイゼンシュタイン級数は\begin{align}G_4(1,i) &=\sum_{m,n}'\frac{1}{(m+ni)^{4}}=\frac{\G(\frac{1}{4})^8}{960\pi^2}\\G_6(1,i) &=\sum_{m,n}'\frac{1}{(m+ni)^{6}}=0\\G_8(1,i) &=\sum_{m,n}'\frac{1}{(m+ni)^{8}}=\frac{\G(\frac{1}{4})^{16}}{2150400\pi^4}\\G_{10}(1,i) &=\sum_{m,n}'\frac{1}{(m+ni)^{10}}=0\\G_{12} (1,i)&=\sum_{m,n}'\frac{1}{(m+ni)^{12}}=\frac{\G(\frac{1}{4})^{24}}{7028736000\pi^6}\\G_{14}(1,i)&=\sum_{m,n}'\frac{1}{(m+ni)^{14}}=0\end{align}
オマケ:定義域が実数のときのペー関数のようす
$\o_1=1$ , $\o_2=i$ とします。定理4の不変量より3次方程式は$$4t^3-\frac{\G(\frac{1}{4})^8}{16\pi^2}t=0$$であるから$$e_1=\a\;,\quad e_2=0\;,\quad e_3=-\a$$と書けます。ただし$$\a:=\frac{\G(\frac{1}{4})^4}{8\pi}=\frac{\sqrt{g_2}}{2}$$よって$$\wp\left(\frac{1}{2}\right)=\a\;,\;\wp\left(\frac{i}{2}\right)=-\a\;,\;\wp\left(\frac{1+i}{2}\right)=0$$いま $z$ を実数 $x\in(0,1)$ に限定します。$\wp'(z)=0$ となるのは $z\equiv \frac{1}{2},\frac{i}{2},-\frac{1+i}{2}$ なる点ですが、いまの定義域では $x=\frac{1}{2}$ のみです。$$\wp(x)=\frac{1}{x^2}+O(x^2)\;,\;\wp'(x)=-\frac{2}{x^3}+O(x)$$なので$$\lim_{x\to+0}\wp(x)=+\infty\;,\quad\lim_{x\to+0}\wp'(x)=-\infty$$です。一方$$\lim_{x\to -0}\wp(x)=+\infty\;,\quad\lim_{x\to -0}\wp'(x)=+\infty$$ですが、これは周期性より$$\lim_{x\to 1-0}\wp(x)=+\infty\;,\quad\lim_{x\to 1-0}\wp'(x)=+\infty$$を導きます。これらから増減表を書くと
| $x$ | $0$ | $\frac{1}{2}$ | $1$ | ||
| $\wp'(x)$ | $-\infty$ | $-$ | $0$ | $+$ | $+\infty$ |
| $\wp(x)$ | $+\infty$ | $\searrow$ | $\a$ | $\nearrow$ | $+\infty$ |
よって $\wp(x)>\a>0$ です。また(0b)を微分して得られる$$\wp''(x)=6\wp(x)^2-2\a^2>4\a^2>0$$より下に凸であり変曲点はありません。
増減表およびこちらの系4から$$\wp\left(\frac{1}{4}\right)=\wp\left(\frac{3}{4}\right)=(\sqrt{2}+1)\frac{\G(\frac{1}{4})^4}{8\pi}$$さらに\begin{align}\wp'\left(\frac{1}{4}\right)^2&=4\wp\left(\frac{1}{4}\right)\left(\wp\left(\frac{1}{4}\right)-\a\right)\left(\wp\left(\frac{1}{4}\right)+\a\right)\\&=8(\sqrt{2}+1)^2\a^3\end{align}$x=3/4$ についても同様にして、その結果$$\wp'\left(\frac{1}{4}\right)=-\frac{(\sqrt{2}+1)\G(\frac{1}{4})^6}{8\pi^{3/2}}\;,\;\wp'\left(\frac{3}{4}\right)=\frac{(\sqrt{2}+1)\G(\frac{1}{4})^6}{8\pi^{3/2}}$$このようにして、何とかペー関数のようすを少しは調べることができました。
次に、不変量が $g_2=0$ , $g_3=1$ のときを考えます。このとき定理1の3次方程式は\begin{equation}4t^3-1=0\tag{11}\end{equation}であり、解は $t=\a$ , $\a e^{\frac{2}{3}\pi i}$ , $\a e^{-\frac{2}{3}\pi i}$ です。ただし $\a=2^{-\frac{2}{3}}$ です。\begin{equation}e_1=\a\;,\quad e_2=\a e^{\frac{2}{3}\pi i}\;,\quad e_3=\a e^{-\frac{2}{3}\pi i}\tag{12}\end{equation}とおきます。
周期の計算
条件が合わないので定理3を直接使うことはできませんが、定理3のもとである(0c)\begin{equation}z=\int_{\wp(z)}^\infty(4t^3-g_2t-g_3)^{-\frac{1}{2}}dt\tag{13}\end{equation}を計算すればOKです。
(12)の3点を複素平面に描いてみると、実軸上の $e_1$ から $+\infty$ に至る経路には特異点はありませんので \begin{equation}\frac{\o_1}{2}=\int_{\a}^{+\infty}(4t^3-1)^{-\frac{1}{2}}dt\tag{14}\end{equation}となり、定理3と同じ式です。$t=\a u$ と置換すると$$=\a\int_1^{+\infty}\frac{du}{\sqrt{u^3-1}}$$$u=1/y$ と置換して$$=\a\int_0^1\frac{dy}{\sqrt{y(1-y^3)}}$$$y^3=x$ とおくと$$=\frac{\a}{3}\int_0^1x^{-\frac{5}{6}}(1-x)^{-\frac{1}{2}}dx=\frac{\a}{3}B\left(\frac{1}{6},\frac{1}{2}\right)$$ガンマ関数を用いることで\begin{equation}\o_1=\frac{\G(\frac{1}{3})^3}{2\pi}\tag{15}\end{equation}
次に $e_2$ についての(13)は\begin{equation}\frac{\o_2}{2}=\int_{\a e^{\frac{2}{3}\pi i}}^{\infty}(4t^3-1)^{-\frac{1}{2}}dt\tag{16}\end{equation}であり、積分経路を $t=re^{\frac{2}{3}\pi i}$ で $r\in [\a,+\infty)$ なる直線に設定します。このとき $t=\a e^{\frac{2}{3}\pi i}u$ と置換して$$\frac{\o_2}{2}=\a e^{\frac{2}{3}\pi i}\int_1^{+\infty}\frac{du}{\sqrt{u^3-1}}=e^{\frac{2}{3}\pi i}\frac{\o_1}{2}$$したがって
$g_2=0$ , $g_3=1$ のとき、対応するペー関数の周期は\begin{equation}\begin{pmatrix}\o_1\\\o_2\end{pmatrix}=\frac{\G(\frac{1}{3})^3}{2\pi}\begin{pmatrix}1\\e^{\frac{2}{3}\pi i}\end{pmatrix}\tag{17}\end{equation}
wolframの「WeierstrassHalfPeriods」で計算すると(17)の $e^{\frac{2}{3}\pi i}$ のところが $e^{\frac{1}{3}\pi i}$ と出ますが、$1+e^{\frac{2}{3}\pi i}=e^{\frac{1}{3}\pi i}$ なので周期の任意性の範囲であり問題ありません。
アイゼンシュタイン級数の値
(17)より次のように書けます。\begin{align}g_2\left(\frac{\G(\frac{1}{3})^3}{2\pi},e^{\frac{2}{3}\pi i}\frac{\G(\frac{1}{3})^3}{2\pi}\right)&=0\tag{18a}\\ g_3\left(\frac{\G(\frac{1}{3})^3}{2\pi},e^{\frac{2}{3}\pi i}\frac{\G(\frac{1}{3})^3}{2\pi}\right)&=1\tag{18b}\end{align}あとは(10)を導出したときと同様に
\begin{equation}g_2(1,\o)=0\;,\quad g_3(1,\o)=\frac{\G(\frac{1}{3})^{18}}{64\pi^6}\tag{19}\end{equation}ただし $\o=e^{\frac{2}{3}\pi i}$ .
定理4と同様にアイゼンシュタイン級数も求めると
$\wp(z)$ の周期が $1$ , $\o$ のとき($\o:=e^{\frac{2}{3}\pi i}$)、不変量は$$g_2(1,\o)=0\;,\quad g_3(1,\o)=\frac{\G(\frac{1}{3})^{18}}{64\pi^6}$$あらわれるアイゼンシュタイン級数は\begin{align}G_4(1,\o) &=\sum_{m,n}'\frac{1}{(m+n\o)^{4}}=0\\G_6(1,\o) &=\sum_{m,n}'\frac{1}{(m+n\o)^{6}}=\frac{\G(\frac{1}{3})^{18}}{8960\pi^6}\\G_8(1,\o) &=\sum_{m,n}'\frac{1}{(m+n\o)^{8}}=0\\G_{10}(1,\o) &=\sum_{m,n}'\frac{1}{(m+n\o)^{10}}=0\\G_{12} (1,\o)&=\sum_{m,n}'\frac{1}{(m+n\o)^{12}}=\frac{\G(\frac{1}{3})^{36}}{459210752\pi^{12}}\\G_{14}(1,\o)&=\sum_{m,n}'\frac{1}{(m+n\o)^{14}}=0\end{align}
次回は:
第5版です。いわずと知れた名著。楕円関数にかなりのページを割いています。

Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。