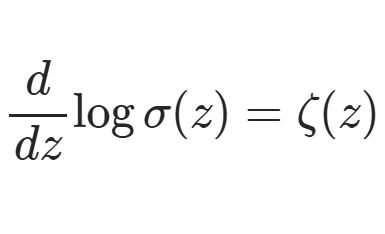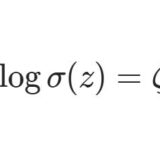ワイエルシュトラスのペー関数６～擬周期性をもつゼータ関数

前回はこちら：

ワイエルシュトラスのペー関数５~周期・不変量・アイゼンシュタイン級数の計算

ワイエルシュトラスのゼータ関数

ワイエルシュトラスのペー関数 $\wp(z)$ は基本周期 $\o_1,\o_2$ をもつ楕円関数で、$z\equiv 0$ すなわち原点および原点と合同な点 $m\o_1+n\o_2$ で2位の極をもつのでした（格子点）。こちらの系５より楕円関数はセル内部に重複を込めて2つ以上の極をもちます。特に $\wp(z)$ はセル内部に $z\equiv0$ を2位の極としてもち、他に極をもたないという楕円関数としては非常にシンプルな性質をもっているのです。

今回は「楕円関数ではないけど、格子点にのみ1位の極をもつような関数」をつくりたい。2位ではなく1位です。そのような楕円関数はありえませんが、楕円関数に類似する性質を保持しつつこのような関数（楕円関数もどき？）をつくるということです。

ペー関数 $\wp(z)$ を積分すると2位の極が1位になるでしょう。そこで\begin{equation}\frac{d\zeta(z)}{dz}=-\wp(z)\;,\;\; \lim_{z\to0 }\left(\zeta(z)-\frac{1}{z}\right)=0\tag{1}\end{equation}なる関数 $\zeta$ を定義します。これをワイエルシュトラスのゼータ関数といいます。$\wp$ の積分によってゼータ関数を定義するため、積分定数が現れますから初期条件を附しています。

なお、有名なリーマンゼータ関数とは関係がありません。

ただちに$$\frac{d\zeta}{dz}+\frac{1}{z^2}=-\left(\wp(z)-\frac{1}{z^2}\right)$$を得てこれを積分します。$$\int_0^z\left(\frac{d\zeta}{dz}+\frac{1}{z^2}\right)dz=-\int_0^z\left(\wp(z)-\frac{1}{z^2}\right)dz$$左辺は(1)の初期条件よりすぐに計算できて$$\zeta(z)-\frac{1}{z}=-\int_0^z\left(\wp(z)-\frac{1}{z^2}\right)dz$$ペー関数の定義は\begin{equation}\wp(z):=\frac{1}{z^2}+\sum_{m,n}'\left[\frac{1}{(z-\O_{m,n})^2}-\frac{1}{\O_{m,n}^{~2}}\right]\tag{2}\end{equation}(ただし$\O_{m,n}:=m\o_1+n\o_2$)でした。これより $\wp(z)-\frac{1}{z^2}$ は関数項級数となっていることが分かりますが、初回の議論でこれが一様収束することが示されました。よって項別積分可能です。\begin{align}\zeta(z)-\frac{1}{z}&=-\int_0^z\sum_{m,n}'\left[\frac{1}{(z-\O_{m,n})^2}-\frac{1}{\O_{m,n}^{~2}}\right]dz\\&=\sum_{m,n}'\int_0^z\left[\frac{-1}{(z-\O_{m,n})^2}+\frac{1}{\O_{m,n}^{~2}}\right]dz\\&=\sum_{m,n}'\left[\frac{1}{z-\O_{m,n}}+\frac{z}{\O_{m,n}^{~2}}\right]_0^z\\&=\sum_{m,n}'\left(\frac{1}{z-\O_{m,n}}+\frac{1}{\O_{m,n}}+\frac{z}{\O_{m,n}^{~2}}\right)\end{align}これをゼータ関数の定義としてもよいです。まとめると

ゼータ関数の極と留数

ゼータ関数は関数項級数を使って定義されています。この級数は $|\O_{mn}|$ が大きければ\begin{align}\left|\frac{1}{z-\O_{m,n}}+\frac{1}{\O_{m,n}}+\frac{z}{\O_{m,n}^{~2}}\right|&=\frac{1}{|\O_{m,n}|}\left|-\left(1-\frac{z}{\O_{m,n}}\right)^{-1}+1+\frac{z}{\O_{m,n}}\right|\\&=\frac{1}{|\O_{m,n}|}O\left(\frac{1}{|\O_{m,n}|^2}\right)\\&=O\left(\frac{1}{|\O_{m,n}|^3}\right)\end{align}初回の議論でこのオーダーのものは特異点を除いて一様収束します。

定義式より特異点は $z=\O_{m,n}$ すなわち $z\equiv 0$ (mod $\o_1,\o_2$) であり、すべて1位の極です。-1次の項 $\frac{1}{z-\O_{m,n}}$ の係数が1であることから、留数はすべて $1$ です。

ゼータ関数の奇関数性

定義１より$$\zeta(-z)=-\frac{1}{z}-\sum_{m,n}'\left(\frac{1}{z+\O_{m,n}}-\frac{1}{\O_{m,n}}+\frac{z}{\O_{m,n}^{~2}}\right)$$$m,n$ を $-m,-n$ としても全体の和は変わりませんので$$=-\frac{1}{z}-\sum_{m,n}'\left(\frac{1}{z-\O_{m,n}}+\frac{1}{\O_{m,n}}+\frac{z}{\O_{m,n}^{~2}}\right)$$したがって

後者については $\zeta'(z)=-\wp(z)$ で $\wp(z)$ が偶関数ですから当然です。

ゼータ関数の擬周期性

$\zeta(z)$ は全平面で極を除き解析的です（有理型関数）。この点は楕円関数と同様の性質です。しかしどのように同一な平行四辺形を並べても、すべての平行四辺形の内部で留数の和が０になることはありません（定理２）。これは楕円関数の性質とは異なります（こちらの定理3）。したがって $\zeta(z)$ は楕円関数ではありません。

しかし周期性こそ崩れたものの、それに近い何らかの法則性は保持されていないでしょうか？

ペー関数の周期性より$$\wp(z+\o_1)=\wp(z)$$すなわち$$\frac{d\zeta(z+\o_1)}{dz}=\frac{d\zeta(z)}{dz}$$つまり定数 $\eta_1$ を用いて$$\zeta(z+\o_1)=\zeta(z)+\eta_1$$と書かれるわけです。$z$ は任意ですから、$\zeta(z)$ は周期性こそもたないけれども１周期ごとに定数が足される性質をもっています。なので「擬周期性(quasi-periodicity)をもつ」ということがあります。

$z=-\o_1/2$ とすると$$\zeta\left(\frac{\o_1}{2}\right)=\zeta\left(-\frac{\o_1}{2}\right)+\eta_1$$であり奇関数性から$$\eta_1=2\zeta\left(\frac{\o_1}{2}\right)$$と求まります。

$\o_2$ についても同様で、現れる定数を $\eta_2$ と書きます。$$\zeta(z+\o_2)=\zeta(z)+\eta_2$$

さらに $\o_3:=-\o_1-\o_2$ についても全く同様にできて定数を $\eta_3$ と書きます。$$\zeta(z+\o_3)=\zeta(z)+\eta_3$$ただし$$\zeta(z+\o_3)=\zeta(z-\o_1-\o_2)=\zeta(z)-\eta_1-\eta_2$$なので $\eta_1+\eta_2+\eta_3=0$ が成立します。

まとめると、

$\o_3$ と $\eta_3$ は独立したものではありませんので不要かもしれませんが、役に立つことがあれば。

ゼータ関数の級数展開

ペー関数の級数展開$$\wp(z)=\frac{1}{z^2}+\sum_{k=1}^\infty(2k+1)G_{2k+2}z^{2k}$$ただし$$G_{2k}:=\sum_{m,n}'\frac{1}{\O_{m,n}^{~2k}}=\sum_{m,n}'\frac{1}{(m\o_1+n\o_2)^{2k}}$$をアイゼンシュタイン級数といいます。そして不変量は$$g_2:=60G_4\;,\quad g_3:=140G_6$$で定義されるのでした。

ペー関数を積分して

ゼータ関数の同次性

ペー関数を周期によって定義する場合と不変量によって定義する場合があるのでした。こちらで見たように\begin{equation}\wp\left(z\left|\begin{matrix}\o_1\\\o_2\end{matrix}\right.\right)\tag{3}\end{equation}とか\begin{equation}\wp(z;g_2,g_3)\tag{4}\end{equation}のように書いてそれを明示しました。

ゼータ関数はペー関数の積分です。なのでペー関数の周期 $\o_1,\o_2$ はそのままゼータ関数の擬周期へ引き継がれます。不変量についても同様です。なのでゼータ関数でも\begin{equation}\zeta\left(z\left|\begin{matrix}\o_1\\\o_2\end{matrix}\right.\right)\tag{5}\end{equation}とか\begin{equation}\zeta(z;g_2,g_3)\tag{6}\end{equation}のように書くことにします。

さて、まず周期によるときには定義１より\begin{align}\zeta\left(\lambda z\left|\begin{matrix}\lambda\o_1\\\lambda\o_2\end{matrix}\right.\right)&=\frac{1}{\lambda z}+\sum_{m,n}'\left(\frac{1}{\lambda z-\lambda\O_{m,n}}+\frac{1}{\lambda\O_{m,n}}+\frac{\lambda z}{\lambda^2\O_{m,n}^{~2}}\right)\\&=\lambda^{-1}\zeta\left(z\left|\begin{matrix}\o_1\\\o_2\end{matrix}\right.\right)\end{align}

一方こちらで得た$$\wp(\lambda z;\lambda^{-4}g_2,\lambda^{-6}g_3)=\lambda^{-2}\wp(z;g_2,g_3)$$を積分することで別の同次性が導けます。

ルジャンドルの関係式

セルを一周する経路を $C$ とします。つまり $z_0$ , $z_0+\o_1$ , $z_0+\o_1+\o_2$ , $z_0+\o_2$ なる基本平行四辺形を周回するということです($z_0$ は平行四辺形の周上に極が来ないように適当にとった点)。

定理２より $\zeta(z)$ は $z\equiv 0$ に1位の極をもちますから、$C$ の内部にも1位の極が1つあります。そしてその留数は $1$ です。よって\begin{equation}\oint_C\zeta(z)dz=2\pi i\tag{7}\end{equation}一方、\begin{align}\oint_C\zeta(z)dz &= \int_{z_0}^{z_0+\o_1}+\int_{z_0+\o_1}^{z_0+\o_1+\o_2}+\int_{z_0+\o_1+\o_2}^{z_0+\o_2}+\int_{z_0+\o_2}^{z_0}\\&=\int_{z_0}^{z_0+\o_1}\zeta(z)dz+\int_{z_0}^{z_0+\o_2}\zeta(z+\o_1)dz+\int^{z_0}_{z_0+\o_1}\zeta(z+\o_2)dz+\int^{z_0}_{z_0+\o_2}\zeta(z)dz\end{align}定理４により$$=\int_{z_0}^{z_0+\o_1}\zeta(z)dz+\int_{z_0}^{z_0+\o_2}(\zeta(z)+\eta_1)dz+\int^{z_0}_{z_0+\o_1}(\zeta(z)+\eta_2)dz+\int^{z_0}_{z_0+\o_2}\zeta(z)dz$$いろいろ打ち消しあって最終的に$$=\eta_1\o_2-\eta_2\o_1$$(7)より$$\eta_1\o_2-\eta_2\o_1=2\pi i$$$\o_1+\o_2+\o_3=0$ および $\eta_1+\eta_2+\eta_3=0$ によって $\o_1$ , $\eta_1$ を消去すると$$\eta_2\o_3-\eta_3\o_2=2\pi i$$となり、さらに $\o_2$ , $\eta_2$ を消去して$$\eta_3\o_1-\eta_1\o_3=2\pi i$$

ゼータ関数の擬加法定理

\begin{equation}f(z):=\frac{\wp'(z)-\wp'(w)}{\wp(z)-\wp(w)}\tag{8}\end{equation}を $z$ の関数とみます。$f(z)$ の極を調べてみましょう。

$\wp(z)$ とその導関数の $z=0$ まわりの展開式は\begin{equation}\wp(z)=\frac{1}{z^2}+O(z^2)\tag{9}\end{equation}\begin{equation}\wp'(z)=-\frac{2}{z^3}+O(z)\tag{10}\end{equation}であることをおさえておきましょう。詳細はこちら。

(9)より $z$ に関する楕円関数 $\wp(z)-\wp(w)$ は $z\equiv 0$ に2位の極をもち、$z\equiv\pm w$ が明らかに零点です。極と零点の個数は等しいので、この零点は1位です。

したがって$\frac{1}{\wp(z)-\wp(w)}$ は $z\equiv\pm w$ に1位の極をもち、$z\equiv 0$ に2位の零点をもちます。

(10)より $\wp'(z)$ は $z\equiv 0$ に3位の極をもちます（1位の零点を３個もつが今は無関係）。したがって楕円関数$$g(z):=\frac{\wp'(z)}{\wp(z)-\wp(w)}$$は $z\equiv 0$ , $\pm w$ の3点に1位の極をもちます。

$g(z)$ を極のまわりに展開します。それぞれの-1次の係数を求めます。\begin{align}\lim_{z\to 0}zg(z) &=\lim_{z\to 0}z\frac{-\frac{2}{z^3}+O(z)}{\frac{1}{z^2}+O(1)}\\&=-2\end{align}$$\lim_{z\to w}(z-w)g(z)=\frac{\wp'(w)}{\wp'(w)}=1$$同様に$$\lim_{z\to -w}(z+w)g(z)=1$$以上よりそれぞれの極まわりの展開式は\begin{align}g(z) &= -\frac{2}{z}+O(1)\tag{11a}\\g(z) &= \frac{1}{z-w}+O(1)\tag{11b}\\g(z)&= \frac{1}{z+w}+O(1)\tag{11c}\end{align}

次に$$h(z):=\frac{\wp'(w)}{\wp(z)-\wp(w)}$$についても極を調べます。$h(z)$ は $z\equiv\pm w$ に1位の極をもちます。$g(z)$ と違って $0$ では正則です。同様にして\begin{align}h(z) &=\frac{1}{z-w}+O(1)\tag{12b}\\h(z)&= -\frac{1}{z+w}+O(1)\tag{12c}\end{align}定義より $f=g-h$ です。よって(11)(12)から $f(z)$ は $z\equiv 0$ , $-w$ に1位の極をもち\begin{align}f(z) &=-\frac{2}{z}+O(1)\tag{13a}\\f(z)&= \frac{2}{z+w}+O(1)\tag{13c}\end{align}定義(8)に立ち返り\begin{equation}\frac{1}{2}\frac{\wp'(z)-\wp'(w)}{\wp(z)-\wp(w)}=\begin{cases}-\dfrac{1}{z}+O(1)\\\dfrac{1}{z+w}+O(1)\end{cases}\tag{14}\end{equation}

ところで $\zeta(z)$ は $z\equiv 0$ に1位の極で留数 $1$ ですから$$\zeta(z)=\frac{1}{z}+O(1)$$と書けます。この事実と(14)を合わせると\begin{equation}F(z):=\frac{1}{2}\frac{\wp'(z)-\wp'(w)}{\wp(z)-\wp(w)}+\zeta(z)-\zeta(z+w)\tag{15}\end{equation}は極をもたないことになります。

さて $F(z)$ は楕円関数でしょうか？周期性を見てみましょう。\begin{align}F(z+\o_1) &=\frac{1}{2}\frac{\wp'(z)-\wp'(w)}{\wp(z)-\wp(w)}+\zeta(z+\o_1)-\zeta(z+\o_1+w)\\&=\frac{1}{2}\frac{\wp'(z)-\wp'(w)}{\wp(z)-\wp(w)}+\zeta(z)+\eta_1-\zeta(z+w)-\eta_1\\&=F(z)\end{align}$\o_2$ についても同様です。つまり $F(z)$ は二重周期をもつ有理型関数なので楕円関数です。

結局 $F(z)$ は極をもたない楕円関数であり、定数関数と結論付けられます。ただしこの定数は $w$ による可能性がありますので$$F(z)=c(w)$$と書けます。ここまでの議論を $z$ と $w$ を取り替えて行うことにより$$F(w)=c(z)$$が成立します。\begin{align}\frac{1}{2}\frac{\wp'(z)-\wp'(w)}{\wp(z)-\wp(w)}+\zeta(z)-\zeta(z+w)&=c(w)\\\frac{1}{2}\frac{\wp'(z)-\wp'(w)}{\wp(z)-\wp(w)}+\zeta(w)-\zeta(z+w)&=c(z)\end{align}ここで $c'(w):=c(w)+\zeta(w)$ と置きなおすと\begin{align}\frac{1}{2}\frac{\wp'(z)-\wp'(w)}{\wp(z)-\wp(w)}+\zeta(z)+\zeta(w)-\zeta(z+w)&=c'(w)\\\frac{1}{2}\frac{\wp'(z)-\wp'(w)}{\wp(z)-\wp(w)}+\zeta(z)+\zeta(w)-\zeta(z+w)&=c'(z)\end{align}この2式の左辺は同じなので $c'$ は $z$ にも $w$ にもよらない定数でなければなりません。$$\frac{1}{2}\frac{\wp'(z)-\wp'(w)}{\wp(z)-\wp(w)}+\zeta(z)+\zeta(w)-\zeta(z+w)=c'$$$z\to -z$ , $w\to -w$ として $c'=0$ と求まります。

以上から

両辺を2乗して左辺には加法定理を適用します。\begin{equation}\wp(z+w)+\wp(z)+\wp(w)=\left[\zeta(z+w)-\zeta(z)-\zeta(w)\right]^2\tag{17}\end{equation}ここで $\a+\b+\g=0$ として\begin{equation}\wp(\a)+\wp(\b)+\wp(\g)=\left[\zeta(\a)+\zeta(\b)+\zeta(\g)\right]^2\tag{18}\end{equation}とも書けます。最後に左辺をゼータ関数で表して

ゼータの微分が混じっており $\zeta$ のみで代数的に表せないことから、れっきとした加法定理とはよべず擬加法定理と名付けています。

参考文献

[1] Whittaker, E. T., & Watson, G. N. (2021). A course of modern analysis. Cambridge University Press.

第５版です。いわずと知れた名著。楕円関数にかなりのページを割いています。

[2] Georgios Pastras (2017), Four Lectures on Weierstrass Elliptic Function and Applications in Classical and Quantum Mechanics ,2024/12/28アクセス

[3] 緒方 秀教. 楕円関数論(10) Weierstrassの楕円関数(2). (2025/1/11アクセス)

応援のおねがい

Please support me!

まめしば

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。

ご支援いただいた方は、こちらで確認できます。

◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。

◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。

OFUSEで応援を送る

◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。