「ゼータ関数の基礎」シリーズ第8回です。前回は:
もくじ
任意の複素数 $s$ に対し$$\zeta(s)\G\left(\frac{s}{2}\right)\pi^{-\frac{s}{2}}-\frac{1}{s(s-1)}=\int_1^\infty(x^{\frac{1-s}{2}}+x^{\frac{s}{2}})\vartheta(x)\frac{dx}{x}$$ただし $\vartheta(x)$ を次のように定義する。$$\vartheta(x)\equiv\sum_{n=1}^\infty e^{-n^2\pi x}$$
今日はこれを導出しましょう。左辺も右辺もあらゆる $s$ において解析的であり、$s$ と $1-s$ が対称であることが分かる等式です。$s$ の実部を $1/2$ とすることでリーマン予想と関係があるのかもしれませんが、踏み込むほどの知識はありません。
左辺が対称であることは過去記事参照
ガンマ関数の定義から$$\G\left(\frac{s}{2}\right)=\int_0^\infty t^{\frac{s}{2}-1}e^{-t}dt$$自然数 $n$ に対して $t=n^2\pi x$ と置換すると$$\G\left(\frac{s}{2}\right)=n^s\pi^{\frac{s}{2}}\int_0^\infty x^{\frac{s}{2}-1}e^{-n^2\pi x}dx$$$$\therefore\quad \G\left(\frac{s}{2}\right) n^{-s}\pi^{-\frac{s}{2}}=\int_0^\infty x^{\frac{s}{2}-1}e^{-n^2\pi x}dx$$
$n=1$ から $N$ まで和をとります。$$\G\left(\frac{s}{2}\right)\pi^{-\frac{s}{2}}\sum_{n=1}^N \frac{1}{n^s}=\int_0^\infty x^{\frac{s}{2}-1}\left(\sum_{n=1}^Ne^{-n^2\pi x}\right)dx$$よって $N\to\infty$ の極限で次の式が成立します。
\begin{equation}\G\left(\frac{s}{2}\right)\zeta(s)\pi^{-\frac{s}{2}}=\displaystyle\lim_{N\to\infty}\int_0^\infty x^{\frac{s}{2}-1}\left(\sum_{n=1}^Ne^{-n^2\pi x}\right)dx\tag{1}\end{equation}
$\sigma\equiv\mathfrak{R}s>2$ とします。
$x\ge 0$ で定義される(1)の被積分関数列を$$f_N(x)\equiv x^{\frac{s}{2}-1}\sum_{n=1}^Ne^{-n^2\pi x}$$とおきます。この関数列は次のように評価できます。\begin{eqnarray*}|f_N(x)|&&\le x^{\frac{\sigma}{2}-1}\sum_{n=1}^N e^{-n^2\pi x}\\&&\le x^{\frac{\sigma}{2}-1}\sum_{n=1}^N e^{-n\pi x}\\&&= x^{\frac{\sigma}{2}-1}\frac{e^{-\pi x}(1-e^{-N\pi x})}{1-e^{-\pi x}}\\&&\le x^{\frac{\sigma}{2}-1}\frac{e^{-\pi x}}{1-e^{-\pi x}}\\&&=\frac{x^{\frac{\sigma}{2}-1}}{e^{\pi x}-1}\equiv g(x)\end{eqnarray*}
よって $|f_N(x)|\le g(x)$ と押さえることができます。ここでゼータ関数の積分表示を用いて$$\int_0^\infty g(x)dx=\int_0^\infty\frac{x^{\frac{\sigma}{2}-1}}{e^{\pi x}-1}dx=\frac{\G(\frac{\sigma}{2})}{\pi^{\frac{\sigma}{2}}}\zeta\left(\frac{\sigma}{2}\right)<+\infty$$よってLebesgueの優収束定理より、(1)の右辺で積分と極限の入れ替えが可能となります。$$\G\left(\frac{s}{2}\right)\zeta(s)\pi^{-\frac{s}{2}}=\int_0^\infty x^{\frac{s}{2}-1}\left(\sum_{n=1}^\infty e^{-n^2\pi x}\right)dx$$
したがって$$\vartheta(x)\equiv\sum_{n=1}^\infty e^{-n^2\pi x}$$と定義すれば
\begin{equation}\G\left(\frac{s}{2}\right)\zeta(s)\pi^{-\frac{s}{2}}=\int_0^\infty x^{\frac{s}{2}-1}\vartheta(x)dx\quad(\sigma>2)\tag{2}\end{equation}
優収束定理については外部の記事を参考にしました:
関数$\psi(x)$と複素積分の定義
$x>0$ で関数 $\psi(x)$ を\begin{equation}\psi(x)\equiv\sum_{n=-\infty}^\infty e^{-n^2\pi x}\tag{3}\end{equation}と定義します(ディガンマ関数も同じ記号だが無関係)。$\vartheta(x)$ の定義と見比べると\begin{equation}\psi(x)=2\vartheta(x)+1\tag{4}\end{equation}なる関係があります。
ここから少し長くなりますが$$\psi(x)=\frac{1}{\sqrt{x}}\psi\left(\frac{1}{x}\right)$$であることを示します。
ここで $\displaystyle\sum_{n=-\infty}^\infty$ は $\displaystyle\lim_{N\to\infty}\sum_{n=-N}^N$ を表します。
次の積分を考えます。$$\oint_{C_N}\frac{e^{-z^2\pi x}}{e^{2\pi iz}-1}dz$$被積分関数は $z=0,\pm1,\pm2\cdots$ に1位の極(pole)をもちます。経路 $C_N$ は下図のように $\pm(N+\frac{1}{2})\pm i$ を頂点とする長方形です。
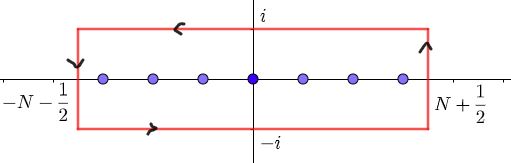
留数計算
留数定理により周回積分の値は\begin{eqnarray*}\oint_{C_N}\frac{e^{-z^2\pi x}}{e^{2\pi iz}-1}dz&&=2\pi i\sum_{n=-N}^N\mathrm{Res}_{z=n}\frac{e^{-z^2\pi x}}{e^{2\pi iz}-1}\\&&=2\pi i\sum_{n=-N}^N\displaystyle\lim_{z\to n}\frac{e^{-z^2\pi x}}{e^{2\pi iz}-1}(z-n)\\&&=2\pi i\sum_{n=-N}^N\displaystyle\lim_{z\to n}\frac{z-n}{e^{2\pi iz}-e^{2\pi i n}}e^{-z^2\pi x}\\&&=\sum_{n=-N}^N e^{-n^2\pi x}\end{eqnarray*}よって $N\to\infty$ としたときの経路を $C$ とすれば
\begin{equation}\psi(x)=\oint_{C}\frac{e^{-z^2\pi x}}{e^{2\pi iz}-1}dz\tag{5}\end{equation}
なる等式が成り立つことになります。
経路を分ける
(5)より$$\psi(x)=\left(\int_{-\infty-i}^{\infty-i}+\int^{\infty+i}_{\infty-i}+\int^{-\infty+i}_{\infty+i}+\int^{-\infty-i}_{-\infty+i}\right)\frac{e^{-z^2\pi x}}{e^{2\pi iz}-1}dz$$
第2項の積分は\begin{eqnarray*}\left|\int^{N+\frac{1}{2}+i}_{N+\frac{1}{2}-i}\frac{e^{-z^2\pi x}}{e^{2\pi iz}-1}dz\right|&&=\left|\int^1_{-1}\frac{e^{-\pi x(N+\frac{1}{2}+it)^2}}{e^{2\pi i(N+\frac{1}{2}+it)}-1}dt\right|\\&&\le\int^1_{-1}\frac{e^{-\pi x(N+\frac{1}{2})^2}e^{\pi xt^2}}{|e^{\pi i}e^{-2\pi t}-1|}dt\\&&\le e^{-\pi x(N+\frac{1}{2})^2}\int^1_{-1}\frac{e^{\pi xt^2}}{1+e^{-2\pi t}}dt\\&&\le e^{-\pi x(N+\frac{1}{2})^2}e^{\pi x}\int^1_{-1}\frac{1}{1+e^{-2\pi t}}dt\\&&\le e^{-\pi x(N+\frac{1}{2})^2}e^{\pi x}\frac{2}{1+e^{-2\pi}}\\&&\xrightarrow[N\to\infty]{}0\end{eqnarray*}
同様に第4項の積分も$$\int^{-N-\frac{1}{2}+i}_{-N-\frac{1}{2}+i}\frac{e^{-z^2\pi x}}{e^{2\pi iz}-1}dz\longrightarrow0$$
したがって
\begin{equation}\psi(x)=\int_{-\infty-i}^{\infty-i}\frac{e^{-z^2\pi x}}{e^{2\pi iz}-1}dz-\int_{-\infty+i}^{\infty+i}\frac{e^{-z^2\pi x}}{e^{2\pi iz}-1}dz\tag{6}\end{equation}
積分の実行
(6)の第1項の積分は\begin{eqnarray*}\int_{-\infty-i}^{\infty-i}\frac{e^{-z^2\pi x}}{e^{2\pi iz}-1}dz&&=\int_{-\infty-i}^{\infty-i}\frac{e^{-z^2\pi x}e^{-2\pi iz}}{1-e^{-2\pi iz}}dz\\&&=\int_{-\infty-i}^{\infty-i}\sum_{n=1}^\infty e^{-2\pi inz-z^2\pi x}dz\end{eqnarray*}指数を平方完成します。\begin{eqnarray*}&&=\sum_{n=1}^\infty e^{-\frac{n^2\pi}{x}}\int_{-\infty-i}^{\infty-i}e^{-\pi x(z+ni/x)^2}dz\\&&=\sum_{n=1}^\infty e^{-\frac{n^2\pi}{x}}\int_{-\infty}^{\infty}e^{-\pi x(z+i(\frac{n}{x}-1))^2}dz\end{eqnarray*}この積分はガウス積分の複素数への拡張に相当します。実軸を含む横長の長方形を考えることで、実数のガウス積分と同じ結果が出ることが証明できます(ここでは省略)。\begin{eqnarray}&&=\sum_{n=1}^\infty e^{-\frac{n^2\pi}{x}}\int_{-\infty}^{\infty}e^{-\pi xz^2}dz\\&&=\frac{1}{\sqrt{x}}\sum_{n=1}^\infty e^{-\frac{n^2\pi}{x}}\\&&=\frac{1}{\sqrt{x}}\sum_{n=-\infty}^{-1} e^{-\frac{n^2\pi}{x}}\tag{7}\end{eqnarray}これが1つめの積分になります。
(6)の第2項の積分も同様にしますが、先ほどは公比 $e^{-2\pi iz}$ で展開したところを次は $e^{2\pi iz}$ で展開します。 \begin{eqnarray}-\int_{-\infty+i}^{\infty+i}\frac{e^{-z^2\pi x}}{e^{2\pi iz}-1}dz&&=\int_{-\infty+i}^{\infty+i}\sum_{n=0}^\infty e^{2\pi inz-z^2\pi x}dz\\&&=\sum_{n=0}^\infty e^{-\frac{n^2\pi}{x}}\int_{-\infty+i}^{\infty+i} e^{-\pi x(z-ni/x)^2}dz\\&&=\frac{1}{\sqrt{x}}\sum_{n=0}^\infty e^{-\frac{n^2\pi}{x}}\tag{8}\end{eqnarray}
(7)(8)を足すと$$\int_{-\infty-i}^{\infty-i}\frac{e^{-z^2\pi x}}{e^{2\pi iz}-1}dz-\int_{-\infty+i}^{\infty+i}\frac{e^{-z^2\pi x}}{e^{2\pi iz}-1}dz=\frac{1}{\sqrt{x}}\sum_{n=-\infty}^{\infty} e^{-\frac{n^2\pi}{x}}$$$\psi(x)$ の定義(3)から$$\int_{-\infty-i}^{\infty-i}\frac{e^{-z^2\pi x}}{e^{2\pi iz}-1}dz-\int_{-\infty+i}^{\infty+i}\frac{e^{-z^2\pi x}}{e^{2\pi iz}-1}dz=\frac{1}{\sqrt{x}}\psi\left(\frac{1}{x}\right)$$
よって(6)と合わせて
\begin{equation}\psi(x)=\frac{1}{\sqrt{x}}\psi\left(\frac{1}{x}\right)\quad(x>0)\tag{9}\end{equation}
複素数版のガウス積分については外部記事を参照:
$x=0$と$\infty$について
(4)を再掲します。$$\psi(x)=2\vartheta(x)+1$$これと(9)より$$\sqrt{x}\vartheta(x)=\vartheta\left(\frac{1}{x}\right)+\frac{1}{2}-\frac{\sqrt{x}}{2}$$一方$$\vartheta(x)\le\sum_{n=1}^\infty e^{-n\pi x}\xrightarrow[]{x\to\infty}0$$となるので$$\displaystyle\lim_{x\to0}\sqrt{x}\vartheta(x)=\frac{1}{2}$$
(2)に戻りましょう。\begin{equation}\G\left(\frac{s}{2}\right)\zeta(s)\pi^{-\frac{s}{2}}=\int_0^\infty x^{\frac{s}{2}-1}\vartheta(x)dx\quad(\sigma>2)\tag{2}\end{equation}(9)を使って変形します。\begin{eqnarray*}\G&&\left(\frac{s}{2}\right)\zeta(s)\pi^{-\frac{s}{2}}\\&&=\int_0^\infty x^{\frac{s}{2}-1}\vartheta(x)dx\\&&=\int_0^1 x^{\frac{s}{2}-1}\vartheta(x)dx+\int_1^\infty x^{\frac{s}{2}-1}\vartheta(x)dx\\&&=\int_0^1 x^{\frac{s}{2}-1}\left(-\frac{1}{2}+\frac{1}{2\sqrt{x}}+\frac{1}{\sqrt{x}}\vartheta\left(\frac{1}{x}\right)\right)dx+\int_1^\infty x^{\frac{s}{2}-1}\vartheta(x)dx\\&&=\left[-\frac{x^{s/2}}{s}+\frac{x^{\frac{s-1}{2}}}{s-1}\right]_0^1+\int_0^1x^{\frac{s}{2}-1}\frac{1}{\sqrt{x}}\vartheta\left(\frac{1}{x}\right)dx+\int_1^\infty x^{\frac{s}{2}-1}\vartheta(x)dx\\&&=-\frac{1}{s}+\frac{1}{s-1}+\int_0^1x^{\frac{s-3}{2}}\vartheta\left(\frac{1}{x}\right)dx+\int_1^\infty x^{\frac{s}{2}-1}\vartheta(x)dx\end{eqnarray*}1つ目の積分で $x$ を $1/x$ に置換します。\begin{eqnarray*}\G&&\left(\frac{s}{2}\right)\zeta(s)\pi^{-\frac{s}{2}}\\&&=-\frac{1}{s}+\frac{1}{s-1}+\int_1^\infty x^{-\frac{s-3}{2}}\vartheta(x)\frac{dx}{x^2}+\int_1^\infty x^{\frac{s}{2}-1}\vartheta(x)dx\\&&=-\frac{1}{s}+\frac{1}{s-1}+\int_1^\infty x^{-\frac{s+1}{2}}\vartheta(x)dx+\int_1^\infty x^{\frac{s}{2}-1}\vartheta(x)dx\\&&=-\frac{1}{s}+\frac{1}{s-1}+\int_1^\infty (x^{-\frac{s+1}{2}}+x^{\frac{s}{2}-1})\vartheta(x)dx\\&&=-\frac{1}{s}+\frac{1}{s-1}+\int_1^\infty (x^{\frac{1-s}{2}}+x^{\frac{s}{2}})\vartheta(x)\frac{dx}{x}\end{eqnarray*}
移項しましょう。すると目標としていた等式を得ます。
\begin{equation}\zeta(s)\G\left(\frac{s}{2}\right)\pi^{-\frac{s}{2}}-\frac{1}{s(s-1)}=\int_1^\infty(x^{\frac{1-s}{2}}+x^{\frac{s}{2}})\vartheta(x)\frac{dx}{x}\tag{10}\end{equation}
$\sigma>2$ を仮定してここまできましたが、等式(10)はあらゆる $s$ で成立します。右辺と左辺に分けて考えましょう(わざわざ移項したのはそのため)。
右辺はあらゆるsで値をとる
(10)の右辺$$\int_1^\infty(x^{\frac{1-s}{2}}+x^{\frac{s}{2}})\vartheta(x)\frac{dx}{x}$$はすべての $s$ で収束することを示します。まず\begin{eqnarray*}\vartheta(x)&&=\sum_{n=1}^\infty e^{-n^2\pi x}\\&&\le\sum_{n=0}^\infty e^{-(n+1)\pi x}\\&&=\frac{e^{-\pi x}}{1-e^{-\pi x}}\\&&\le\frac{e^{-\pi x}}{1-e^{-\pi}}\quad(\because x\ge 1)\end{eqnarray*}よって $x$ によらない定数 $K$ によって$$\vartheta(x)\le Ke^{-\pi x}$$と押さえることができます。
これを用いて積分を評価しましょう。\begin{eqnarray*}\left|\int_1^\infty(x^{\frac{1-s}{2}}+x^{\frac{s}{2}})\vartheta(x)\frac{dx}{x}\right|&&\le\int_1^\infty(x^{\frac{1-\sigma}{2}}+x^{\frac{\sigma}{2}})\vartheta(x)\frac{dx}{x}\\&&\le K\int_1^\infty(x^{\frac{1-\sigma}{2}}+x^{\frac{\sigma}{2}})e^{-\pi x}\frac{dx}{x}\\&&=K\int_1^\infty(x^{-\frac{1+\sigma}{2}}+x^{\frac{\sigma-2}{2}})e^{-\pi x}dx\end{eqnarray*}$x\ge1$ であるため、$$x^{-\frac{1+\sigma}{2}}+x^{\frac{\sigma-2}{2}}\le 2x^p\quad,\quad p=\lceil\max\left(-\frac{1+\sigma}{2},\frac{\sigma-2}{2}\right)\rceil$$なる自然数 $p$ をとれます。
また $x^p\le p!e^x$ ですから\begin{eqnarray*}\left|\int_1^\infty(x^{\frac{1-s}{2}}+x^{\frac{s}{2}})\vartheta(x)\frac{dx}{x}\right|&&\le K\int_1^\infty(x^{-\frac{1+\sigma}{2}}+x^{\frac{\sigma-2}{2}})e^{-\pi x}dx\\&&\le K\int_1^\infty 2x^p e^{-\pi x}dx\\&&\le 2K\cdot p!\int_1^\infty e^{-(\pi-1) x}dx\\&&<+\infty\end{eqnarray*}よってあらゆる $s$ に対して積分は収束し値をとります!
左辺はあらゆるsで値をとる
(10)の左辺はどうでしょうか。$$\zeta(s)\G\left(\frac{s}{2}\right)\pi^{-\frac{s}{2}}-\frac{1}{s(s-1)}$$問題となる点を挙げておきます。まず分数があるので明らかに $s=0,1$ が怪しい。$\zeta(s)$ は $s=1$ に極を、$\G(s/2)$ は$s=0,-2,-4\cdots$ に極をもつので、それらも怪しいです。
したがって調べるべきは $s=0,1,-2m$ です($m\in\NN$)。結論をいうとこれはすべて極限をとれば定義できる除去可能特異点(removable singularity)です。
s=0を調べる
$s\to0$ の極限を考えます。$\zeta(0)=-1/2$ に留意します。\begin{eqnarray*}\displaystyle\lim_{s\to0}&&\left[\zeta(s)\G\left(\frac{s}{2}\right)\pi^{-\frac{s}{2}}-\frac{1}{s(s-1)}\right]\\&&=\displaystyle\lim_{s\to0}\left[-\frac{1}{2}\G\left(\frac{s}{2}\right)+\frac{1}{s}\right]+1\\&&=\displaystyle\lim_{s\to0}\left[-\frac{1}{s}\G\left(\frac{s}{2}+1\right)+\frac{1}{s}\right]+1\\&&=-\frac{1}{2}\displaystyle\lim_{s\to0}\left[\frac{\G\left(\frac{s}{2}+1\right)-\G(1)}{\frac{s}{2}}\right]+1\\&&=-\frac{1}{2}\G'(1)+1\\&&=1+\frac{\g}{2}\end{eqnarray*}ちゃんと値をとることが分かります。
s=1を調べる
$s\to1$ の極限を考えます。\begin{eqnarray*}\displaystyle\lim_{s\to1}&&\left[\zeta(s)\G\left(\frac{s}{2}\right)\pi^{-\frac{s}{2}}-\frac{1}{s(s-1)}\right]\\&&=\displaystyle\lim_{s\to1}\left[\zeta(s)-\frac{1}{s-1}\right]+1\\&&=1+\g\end{eqnarray*}ちゃんと値をとることが分かります。
s=-2mを調べる
$s$ が負の偶数となる極限 $s\to -2m$ を考えます。ガンマ関数が1位の極をもち、ゼータ関数が1位の零点をもつため、相殺されて値をとると予想できますが、ちゃんとやってみます。
$\frac{1}{s(s-1)}$ は問題ないので省きます。過去記事で導出した関数等式や倍数公式を駆使しましょう。\begin{eqnarray*}\displaystyle\lim_{s\to -2m}&&\left[\zeta(s)\G\left(\frac{s}{2}\right)\pi^{-\frac{s}{2}}\right]\\&&=\pi^{m}\lim_{s\to -2m}\zeta(s)\G\left(\frac{s}{2}\right)\\&&=\pi^{m}\lim_{s\to -2m}2^{s-1}\pi^s\frac{\zeta(1-s)}{\G(s)\cos\frac{\pi s}{2}}\G\left(\frac{s}{2}\right)\\&&=\frac{(-1)^m\zeta(2m+1)}{2^{2m+1}\pi^{m}}\lim_{s\to -2m}\frac{\G\left(\frac{s}{2}\right)}{\G(s)}\\&&=\frac{(-1)^m\zeta(2m+1)}{2^{2m+1}\pi^{m}}\lim_{s\to -2m}\frac{\sqrt{\pi}}{2^{s-1}\G(\frac{s+1}{2})}\\&&=\frac{(-1)^m\zeta(2m+1)}{\pi^{m-\frac{1}{2}}}\lim_{s\to -2m}\frac{1}{\G(\frac{s+1}{2})}\\&&=\frac{(-1)^m\zeta(2m+1)}{\pi^{m-\frac{1}{2}}}\frac{1}{\G(-m+\frac{1}{2})}\\&&=\frac{(2m)!\zeta(2m+1)}{(4\pi)^mm!}\end{eqnarray*}値をちゃんととっています。
以上から(10)の左辺はあらゆる $s$ で解析的です!総合すると(10)は全平面で成り立つ式ということになります。
よって今日の結論を得ます。
全平面で以下の等式が成り立つ\begin{equation}\zeta(s)\G\left(\frac{s}{2}\right)\pi^{-\frac{s}{2}}-\frac{1}{s(s-1)}=\int_1^\infty(x^{\frac{1-s}{2}}+x^{\frac{s}{2}})\vartheta(x)\frac{dx}{x}\tag{11}\end{equation}
(11)に $\dfrac{s(s-1)}{2}$ をかけて移項します。$$\frac{s(s-1)}{2}\zeta(s)\G\left(\frac{s}{2}\right)\pi^{-\frac{s}{2}}=\frac{1}{2}+\frac{s(s-1)}{2}\int_1^\infty(x^{\frac{1-s}{2}}+x^{\frac{s}{2}})\vartheta(x)\frac{dx}{x}$$左辺はリーマンのクシー関数 $\xi(s)$ そのものです。$\xi(s)=\xi(1-s)$ という等式は有名です。
\begin{equation}\xi(s)=\frac{1}{2}+\frac{s(s-1)}{2}\int_1^\infty(x^{\frac{1-s}{2}}+x^{\frac{s}{2}})\vartheta(x)\frac{dx}{x}\tag{12}\end{equation}
これもやはり全平面で成立します。
実部を $1/2$ とした場合を考えます。$s=\frac{1}{2}+it$ としましょう(Critical Line)。(12)は\begin{eqnarray*}\xi\left(\frac{1}{2}+it\right)&&=\frac{1}{2}-\frac{1}{2}\left(t^2+\frac{1}{4}\right)\int_1^\infty(x^{\frac{1}{4}-i\frac{t}{2}}+x^{\frac{1}{4}+i\frac{t}{2}})\vartheta(x)\frac{dx}{x}\\&&=\frac{1}{2}-\frac{1}{2}\left(t^2+\frac{1}{4}\right)\int_1^\infty x^{-\frac{3}{4}}(x^{-i\frac{t}{2}}+x^{i\frac{t}{2}})\vartheta(x)dx\\&&=\frac{1}{2}-\left(t^2+\frac{1}{4}\right)\int_1^\infty x^{-\frac{3}{4}}\cos\left(\frac{t}{2}\log x\right)\vartheta(x)dx\end{eqnarray*}
次回はこちら:
ゼータ関数の基礎シリーズ第1回はこちらから:
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。