$p+q>1$ のとき\begin{equation}\int_0^\frac{\pi}{2}\cos^{p+q-2}\t\cos(p-q)\t d\t=\frac{\pi}{2^{p+q-1}(p+q-1)B(p,q)}\tag{1}\end{equation}※最後に $\sin$ バージョンも紹介
ベータ関数の逆数の積分表示を導出します。これはWhittaker-Watsonの第12章、章末の問題39で現れる等式です。
スキャンが悪くて(?)見えにくいですが、要はこうです。
$\pm i$ を両端とする線分および $|z|=1$ の右半円を描く。これより $-i,0,i$ をくりぬいてできる閉曲線を $C$ とする。$\displaystyle\int_C z^{p-q-1}(z+z^{-1})^{p+q-2}dz$ なる積分を考えることにより、$p+q>1$ , $q<1$ ならば$$\int_0^\frac{\pi}{2}\cos^{p+q-2}\t\cos(p-q)\t d\t=\frac{\pi}{2^{p+q-1}(p+q-1)B(p,q)}$$であることを示せ。またこの式は $p+q>1$ を満たすあらゆる $p$ , $q$ で成立することを示せ。
ではこの問題について考えてみましょう。
古いですが有名な書物で、どんどん改訂版が出ています。前半は解析学一般、後半は特殊関数という内容で、網羅的に勉強できます。演習問題に解答がないのが昔ながらのものって感じ。2022/11/6現在、最新版は5th Editionで私も所有していますが、廉価な3rdとかでも十分かと。

A Course of Modern Analysis: fifth Edition

A Course of Modern Analysis: Third Edition
計算する積分と経路は下のようになります。
\begin{equation}\int_C z^{p-q-1}(z+z^{-1})^{p+q-2}dz=\int_{\G_1+\G_2+\G_3+\G_4+\G_5+\G_6}\tag{2}\end{equation}
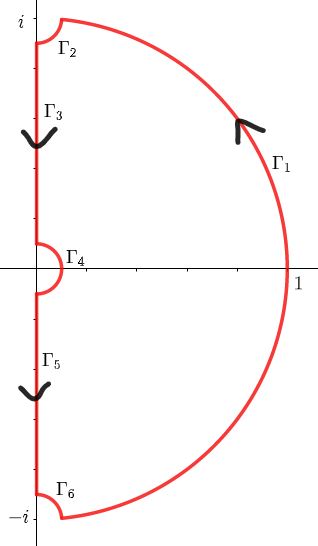
$\G_1$ は半径 $1$ の半円です。$\G_2$ と $\G_6$ は非常に小さな半径 $\epsilon$ の四分円です。先にざっくり言っておくと、半円 $\G_1$ と直線 $\G_3$ , $\G_5$ が求める等式のモトとなり、小円3つは積分値がゼロになります。
右半円なので $z=e^{i\t}$ , $dz=ie^{i\t}$ として\begin{eqnarray*}\int_{\Gamma_1}&&z^{p-q-1}(z+z^{-1})^{p+q-2}dz \\&&= i\int_{-\frac{\pi}{2}}^\frac{\pi}{2}e^{i(p-q)\t}(e^{i\t}+e^{-i\t})^{p+q-2}d\t\\&&=i2^{p+q-2}\int_{-\frac{\pi}{2}}^\frac{\pi}{2}e^{i(p-q)\t}\cos^{p+q-2}\t d\t\end{eqnarray*}積分範囲を $[-\frac{\pi}{2},0]$ と $[0,\frac{\pi}{2}]$ に分け、前者で $\t\to -\t$ と置換することにより\begin{eqnarray*}&&=i2^{p+q-2}\int_0^\frac{\pi}{2}\left(e^{i(p-q)\t}+e^{-i(p-q)\t}\right)\cos^{p+q-2}\t d\t\\&&=i2^{p+q-1}\int_0^\frac{\pi}{2}\cos(p-q)\t\cos^{p+q-2}\t d\t\end{eqnarray*}従って次の式を得ます。
\begin{equation}\int_{\Gamma_1}z^{p-q-1}(z+z^{-1})^{p+q-2}dz=i2^{p+q-1}\int_0^\frac{\pi}{2}\cos^{p+q-2}\t \cos(p-q)\t d\t\tag{3}\end{equation}
経路 $\G_3$ , $\G_4$ , $\G_5$ において $z=xe^{i\t}$ とおきます。$\G_3$ では $\t=\frac{\pi}{2}$ で $x$ は $1$ から $0$ へ変化します。$\G_4$ では $x=\epsilon$ で $\t$ は $\frac{\pi}{2}$ から $0$ を経て $-\frac{\pi}{2}$ まで変化します。$\G_5$ では $\t=-\frac{\pi}{2}$ で $x$ は $0$ から $1$ へ変化します。
\begin{eqnarray*}\int_{\Gamma_3}&&z^{p-q-1}(z+z^{-1})^{p+q-2}dz\\&&=\int_{\Gamma_3}z^{1-2q}(z^2+1)^{p+q-2}dz\\&&=\int_1^0(xe^{\frac{\pi}{2}i})^{1-2q}\left((xe^{\frac{\pi}{2}i})^2+1\right)^{p+q-2}e^{\frac{\pi}{2}i}dx\\&&=-ie^{(\frac{\pi}{2}-\pi q)i}\int_0^1x^{1-2q}(1-x^2)^{p+q-2}dx\\&&=e^{-\pi qi}\int_0^1x^{1-2q}(1-x^2)^{p+q-2}dx\\&&=\frac{e^{-\pi qi}}{2}\int_0^1y^{-q}(1-y)^{p+q-2}dy\quad(y=x^2)\\&&=\frac{e^{-\pi qi}}{2}B(1-q,p+q-1)\end{eqnarray*}$p+q>1$ , $q<1$ を仮定していますので、最後の等式が成立します。
次に $\G_5$ を計算します。\begin{eqnarray*}\int_{\Gamma_5}&&z^{p-q-1}(z+z^{-1})^{p+q-2}dz\\&&=\int_{\Gamma_5}z^{1-2q}(z^2+1)^{p+q-2}dz\\&&=\int_0^1(xe^{-\frac{\pi}{2}i})^{1-2q}\left((xe^{-\frac{\pi}{2}i})^2+1\right)^{p+q-2}e^{-\frac{\pi}{2}i}dx\\&&=-ie^{(-\frac{\pi}{2}+\pi q)i}\int_0^1x^{1-2q}(1-x^2)^{p+q-2}dx\\&&=-e^{\pi qi}\int_0^1x^{1-2q}(1-x^2)^{p+q-2}dx\\&&=-\frac{e^{\pi qi}}{2}\int_0^1y^{-q}(1-y)^{p+q-2}dy\quad(y=x^2)\\&&=-\frac{e^{\pi qi}}{2}B(1-q,p+q-1)\end{eqnarray*}
以上より$$\int_{\Gamma_3+\G_5}z^{p-q-1}(z+z^{-1})^{p+q-2}dz=\frac{e^{-\pi qi}-e^{\pi qi}}{2}B(1-q,p+q-1)$$となりますので、結局次の等式が成り立ちます。
\begin{equation}\int_{\Gamma_3+\G_5}z^{p-q-1}(z+z^{-1})^{p+q-2}dz=-i\sin\pi qB(1-q,p+q-1)\tag{4}\end{equation}
残りの $\G_4$ は $z=\epsilon e^{i\t}$ として\begin{eqnarray*}&&\hskip -2em\left|\int_{\Gamma_4}z^{p-q-1}(z+z^{-1})^{p+q-2}dz\right|\\&&=\left|\int_{\Gamma_4}z^{1-2q}(z^2+1)^{p+q-2}dz\right|\\&&\le\int_{-\frac{\pi}{2}}^\frac{\pi}{2}\epsilon^{2-2q}\left|1+\epsilon^2e^{2i\t}\right|^{p+q-2}d\t\\&&=\epsilon^{2-2q}\int_{-\frac{\pi}{2}}^\frac{\pi}{2}\frac{|1+\epsilon^2e^{2i\t}|^{p+q-1}}{|1+\epsilon^2e^{2i\t}|}d\t\\&&\le\epsilon^{2-2q}\int_{-\frac{\pi}{2}}^\frac{\pi}{2}\frac{(1+\epsilon^2)^{p+q-1}}{1-\epsilon^2}d\t\\&&\xrightarrow[\epsilon\to 0]{}0\quad(\because q<1)\end{eqnarray*}よって
\begin{equation}\int_{\Gamma_4}z^{p-q-1}(z+z^{-1})^{p+q-2}dz=0\tag{5}\end{equation}
最後は $\G_2$ と $\G_6$ です。$\G_4$ と似た方法で示すことができます。
ここでは $\G_2$ のみやります。$z=i+\epsilon e^{i\t}$ と置換して\begin{eqnarray*}&&\hskip -2em\left|\int_{\Gamma_2}z^{p-q-1}(z+z^{-1})^{p+q-2}dz\right|\\&&=\left|\int_{\Gamma_2}z^{1-2q}(z^2+1)^{p+q-2}dz\right|\\&&\le\int_{-\frac{\pi}{2}}^0\left|\epsilon^{p+q-1}(i+\epsilon e^{i\t})^{1-2q}(2i+\epsilon e^{i\t})^{p+q-2}\right|d\t\\&&\le\epsilon^{p+q-1}\int_{-\frac{\pi}{2}}^0\frac{|i+\epsilon e^{i\t}|^{2-2q}|2i+\epsilon e^{i\t}|^{p+q-1}}{|i+\epsilon e^{i\t}||2i+\epsilon e^{i\t}|}d\t\\&&\le\epsilon^{p+q-1}\int_{-\frac{\pi}{2}}^0\frac{(1+\epsilon)^{2-2q}(2+\epsilon)^{p+q-1}}{(1-\epsilon)(2-\epsilon )}d\t\\&&\xrightarrow[\epsilon\to 0]{}0\quad(\because p+q>1)\end{eqnarray*}
$\G_6$ も同様にゼロとなるので
\begin{equation}\int_{\Gamma_2+\G_6}z^{p-q-1}(z+z^{-1})^{p+q-2}dz=0\tag{6}\end{equation}
(3)(4)(5)(6)および $C$ の内部に特異点がないことから、$$i2^{p+q-1}\int_0^\frac{\pi}{2}\cos^{p+q-2}\t \cos(p-q)\t d\t-i\sin\pi qB(1-q,p+q-1)=0$$よって\begin{eqnarray*}\int_0^\frac{\pi}{2}\cos^{p+q-2}\t \cos(p-q)\t d\t&&=\frac{\sin\pi q}{2^{p+q-1}}B(1-q,p+q-1)\\&&=\frac{\sin\pi q}{2^{p+q-1}}\frac{\G(1-q)\G(p+q-1)}{\G(p)}\\&&=\frac{\sin\pi q}{2^{p+q-1}(p-q+1)}\frac{\G(1-q)\G(p+q)}{\G(p)}\end{eqnarray*}相反公式により\begin{eqnarray*}&&=\frac{\pi}{2^{p+q-1}(p-q+1)}\frac{\G(p+q)}{\G(p)\G(q)}\\&&=\frac{\pi}{2^{p+q-1}(p+q-1)B(p,q)}\end{eqnarray*}
これで冒頭の公式が導出できました!
$p+q>1$ のとき\begin{equation}\int_0^\frac{\pi}{2}\cos^{p+q-2}\t\cos(p-q)\t d\t=\frac{\pi}{2^{p+q-1}(p+q-1)B(p,q)}\tag{7}\end{equation}
ここまで $q<1$ なる条件を課していましたが、右辺はこの条件を外しても値をとります。
(7)で $s=p+q-1>0$ 、$p-q=a$ とすると
$s>0$ のとき\begin{equation}\int_0^\frac{\pi}{2}\cos^{s-1}\t\cos a\t d\t=\frac{\pi}{2^{s}sB(\frac{s+a+1}{2},\frac{s-a+1}{2})}\tag{8}\end{equation}
左辺から $\cos^{s-1}\t$ のフーリエ級数展開ができそうです→記事にしました。こちら:
コサインの実数乗(cosθ)^μをフーリエ級数展開(ベータ関数の逆数の積分表示を応用)
さらなる応用の記事!
$$\int_0^\pi\sin^{s-1}\t\sin a\t d\t=\frac{\pi\sin\frac{\pi a}{2}}{2^{s-1}sB(\frac{s+a+1}{2},\frac{s-a+1}{2})}$$$$\int_0^\pi\sin^{s-1}\t\cos a\t d\t=\frac{\pi\cos\frac{\pi a}{2}}{2^{s-1}sB(\frac{s+a+1}{2},\frac{s-a+1}{2})}$$
周回積分$$\int_Cz^{p-q-1}\left(\frac{1}{z}-z\right)^{p+q-2}dz$$とします。分岐点は $0,\pm1$ なので上の図を $+90$度回転させたものを $C$ とします。また $0<\arg z<\pi$ とします。
小さな円弧3か所での積分値は同様に $0$ となります。
半径 $1$ の半円では $z=e^{i\t}$ と置換しますが、この経路において $\arg(\frac{1}{z}-z)=-\frac{\pi}{2}$ であることに注意します(図を描けばすぐ分かります)。\begin{eqnarray*}\int_{\G_1}&&=i\int_0^\pi e^{i(p-q)\t}\left(2e^{-\frac{\pi}{2}i}\sin\t\right)^{p+q-2}d\t\\&&=-i e^{-\frac{p+q}{2}\pi i}2^{p+q-2}\int_0^\pi e^{i(p-q)\t}\sin^{p+q-2}\t d\t\end{eqnarray*}
$\G_3$ においては $z=xe^{i\pi}$ , $\G_5$ においては $z=x$ とおきます。\begin{eqnarray*}\int_{\G_3}&&=\int_1^0(xe^{i\pi})^{1-2q}\left(1-x^2\right)^{p+q-2}e^{i\pi}dx\\&&=-e^{-2i\pi q}\int_0^1x^{1-2q}(1-x^2)^{p+q-2}dx\\&&=-\frac{1}{2}e^{-2i\pi q}B(1-q,p+q-1)\end{eqnarray*}
\begin{eqnarray*}\int_{\G_5}&&=\int_0^1x^{1-2q}(1-x^2)^{p+q-2}dx\\&&=\frac{1}{2}B(1-q,p+q-1)\end{eqnarray*}
$\displaystyle\int_{\G_1}+\displaystyle\int_{\G_3}+\displaystyle\int_{\G_5}=0$ なので相反公式等を使って変形すると$$\int_0^\pi \sin^{p+q-2}\t e^{i(p-q)\t} d\t=\frac{\pi e^{i\frac{p-q}{2}\pi}}{2^{p+q-2}(p+q-1)B(p,q)}$$$p+q-1=s$ , $p-q=a$ とおいて実部虚部をそれぞれとると$$\int_0^\pi\sin^{s-1}\t\sin a\t d\t=\frac{\pi\sin\frac{\pi a}{2}}{2^{s-1}sB(\frac{s+a+1}{2},\frac{s-a+1}{2})}$$$$\int_0^\pi\sin^{s-1}\t\cos a\t d\t=\frac{\pi\cos\frac{\pi a}{2}}{2^{s-1}sB(\frac{s+a+1}{2},\frac{s-a+1}{2})}$$が得られます。
今回現れた公式で、$\phi=\frac{\pi}{2}-\t$ とか $\phi=\pi-\t$ とか試してみてもいいと思います。
ガンマ関数の逆数の積分表示はこちら:
「ガンマ関数の基礎」シリーズ第1回はこちら:
ベータ関数の微分と超幾何関数についてはこちら:
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。





