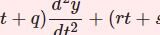ルジャンドル多項式にはいろいろな表現があり，積分表示もその１つです．今日はschlaefliの積分表示といわれるものを導出します．とある複素積分からルジャンドル多項式のロドリグの公式を用いるという手法です．
そもそもルジャンドル多項式とは何？という場合は以下を参照ください．
\begin{equation}P_n(z)=\frac{1}{2\pi i}\oint_C\frac{(t^2-1)^n}{2^n(t-z)^{n+1}}dt\quad(n\in\mathbb{Z^+})\tag{1}\end{equation}ただし $C$ は $z$ 回りを1周する小さな円．$z\neq -1$．
右辺の積分を計算していくのがポイントです．
(1)の右辺をみて$$f(t)\equiv \frac{(t^2-1)^n}{(t-z)^{n+1}} $$ とします．$z\neq\pm1$ とすれば $f(t)$ は $t=z$ で $n+1$ 位の極です．よってローラン展開すると$$f(t)=\frac{a_{-n-1}}{(t-z)^{n+1}}+\frac{a_{-n}}{(t-z)^n}+\cdots+\frac{a_{-1}}{t-z}+\cdots$$$t=z$ まわりを1周する小さな円 $C$ に沿って線積分すると $-1$ 次の項以外はゼロであり $$\oint_Cf(t)dt=2\pi i a_{-1}$$\begin{equation}\therefore\quad a_{-1}=\frac{1}{2\pi i} \oint_Cf(t)dt \tag{2}\end{equation}ここで $f(t)$ に $(t-z)^{n+1}$ かけると$$(t-z)^{n+1}f(t)=a_{-n-1}+a_{-n}(t-z)+\cdots+a_{-1}(t-z)^n+\cdots$$右辺は $t=z$ のテイラー展開の形となっています．両辺を $n$ 回微分すると $n-1$ 次以下の項はゼロになることに注意して$$\frac{d^n}{dt^n}\left[(t-z)^{n+1}f(t)\right]=n!a_{-1}+(n+1)!a_0(t-z)+\cdots$$両辺に $t=z$ を代入すると右辺は第1項のみ残って$$\left.\frac{d^n}{dt^n}\left[(t-z)^{n+1}f(t)\right]\right|_{t=z}=n!a_{-1} $$よって $f(t)$ の定義から$$\left.\frac{d^n}{dt^n}\left[ (t^2-1)^n \right]\right|_{t=z}=n!a_{-1}$$\begin{equation}\therefore\quad \frac{d^n}{dz^n}\left[ (z^2-1)^n\right] = n!a_{-1} \tag{3}\end{equation}
ロドリグの公式は$$P_n(z)=\frac{1}{2^nn!}\frac{d^n}{dz^n}\left[ (z^2-1)^n \right]$$というものです．これと(3)から$$ P_n(z)= \frac{1}{2^nn!}n!a_{-1}=\frac{a_{-1}}{2^n}$$(2)より$$P_n(z)= \frac{1}{2^n} \frac{1}{2\pi i} \oint_Cf(t)dt $$
$$\therefore\quad P_n(z)=\frac{1}{2\pi i}\oint_C\frac{(t^2-1)^n}{2^n(t-z)^{n+1}}dt$$と冒頭の公式ができました！
先ほど $z\neq\pm 1$ と仮定していました．$z=\pm 1$ のときは(1)の右辺は$$ \frac{1}{2\pi i}\oint_C\frac{(t\pm 1)^n}{2^n(t\mp 1)}dt$$複号同順です．ローラン展開$$ \frac{(t\pm1)^n}{t\mp 1} =\frac{a_{-1}}{t\mp 1}+a_0+a_1(t\mp1)+\cdot$$より積分で $-1$ 次の項だけ残り$$\oint_C \frac{(t\pm1)^n}{t\mp 1} dt=2\pi ia_{-1}$$またローラン展開に $t\mp 1$ をかけて $t=\pm1$ を代入すると $a_{-1}=2^n$ を得ますので$$\frac{1}{2\pi i}\oint_C\frac{(t\pm1)^n}{2^n(t\mp 1)}dt=1 $$ということは $P_n(1)=1$ ですので $z=1$ では(1)が成立しますが $P_n(-1)$ は$1$とは限らないので $z=-1$ ではダメです．
『岩波数学公式III』によるとルジャンドル多項式のみならず一般のルジャンドル関数 $P_\nu(z)$ についても成り立つようです．いずれ検討したいです．
ルジャンドル関数の記事：
Please support me!
記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。
