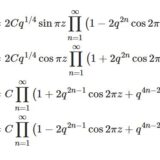前回はこちら:
\begin{align}\begin{split}2w' &=-w+x+y+z\\2x' &=w-x+y+z\\2y' &=w+x-y+z\\2z' &=w+x+y-z\end{split}\tag{0}\end{align}なる関係をもつ場合に\begin{align}\begin{split}[r] & :=\vartheta_r(w)\vartheta_r(x)\vartheta_r(y)\vartheta_r(z)\\[1em] [r]' & :=\vartheta_r(w')\vartheta_r(x')\vartheta_r(y')\vartheta_r(z')\end{split}\end{align}を定義しました。
前回得た定理
\begin{align}2\:[1] &=[1]'+[2]'-[3]'+[4]'\tag{1}\\[1em] 2\:[2] &=[1]'+[2]'+[3]'-[4]'\tag{2}\\[1em] 2\:[3] &=-[1]'+[2]'+[3]'+[4]'\tag{3}\\[1em] 2\:[4] &=[1]'-[2]'+[3]'+[4]'\tag{4}\end{align}
(1)と(2)を辺々足すと$$[1]+[2]=[1]'+[2]'$$となります。他も同様にすると
\begin{align}[1]+[2]&=[1]'+[2]'\tag{5}\\[1em] [2]+[3]&=[2]'+[3]'\tag{6}\\[1em] [1]+[4]&=[1]'+[4]'\tag{7}\\[1em] [3]+[4]&=[3]'+[4]'\tag{8}\\[1em] [1]+[3]&=[2]'+[4]'\tag{9}\\[1em] [2]+[4]&=[1]'+[3]'\tag{10}\\[1em]\end{align}
辺々引いた場合は次のようになります。
\begin{align}[1]-[2]&=[4]'-[3]'\tag{11}\\[1em] [2]-[3]&=[1]'-[4]'\tag{12}\\[1em] [1]-[4]&=[2]'-[3]'\tag{13}\\[1em] [3]-[4]&=[2]'-[1]'\tag{14}\\[1em] [1]-[3]&=[1]'-[3]'\tag{15}\\[1em] [2]-[4]&=[2]'-[4]'\tag{16}\end{align}
系1と系2は4個のテータ関数の積を項としたときの、4項間関係式になっています。系2は系1からでも導出できます。
(0)における $w,x,y$ を $z$ とし、(0)における $z$ を $3z$ とします。すると $w'=x'=y'=2z$ , $z'=0$ となります。$\vartheta_1(0)=0$ なので $[1]'=0$ となることを活用すると、系1と系2のうち $[1]'$ が現れるものを選んで3倍公式をつくることができます。
\begin{align}\vartheta_1^{~3}(z)\vartheta_1(3z)+\vartheta_2^{~3}(z)\vartheta_2(3z)&=\vartheta_2\vartheta_2^{~3}(2z)\tag{17}\\[1em] \vartheta_1^{~3}(z)\vartheta_1(3z)+\vartheta_4^{~3}(z)\vartheta_4(3z)&=\vartheta_4\vartheta_4^{~3}(2z)\tag{18}\\[1em] \vartheta_2^{~3}(z)\vartheta_2(3z)+\vartheta_4^{~3}(z)\vartheta_4(3z)&=\vartheta_3\vartheta_3^{~3}(2z)\tag{19}\\[1em] \vartheta_3^{~3}(z)\vartheta_3(3z)-\vartheta_2^{~3}(z)\vartheta_2(3z)&=\vartheta_4\vartheta_4^{~3}(2z)\tag{20}\\[1em] \vartheta_3^{~3}(z)\vartheta_3(3z)-\vartheta_4^{~3}(z)\vartheta_4(3z)&=\vartheta_2\vartheta_2^{~3}(2z)\tag{21}\\[1em] \vartheta_3^{~3}(z)\vartheta_3(3z)-\vartheta_1^{~3}(z)\vartheta_1(3z)&=\vartheta_3\vartheta_3^{~3}(2z)\tag{22}\end{align}
$[r]$ はテータ関数 $\vartheta_r(\cdot)$ を4つかけたものでした。もっと一般的なものとして次のような定義もできるでしょう。\begin{align}\begin{split}[abcd] & :=\vartheta_a(w)\vartheta_b(x)\vartheta_c(y)\vartheta_d(z)\\[1em] [abcd]' & :=\vartheta_a(w')\vartheta_b(x')\vartheta_c(y')\vartheta_d(z')\end{split}\tag{23}\end{align}例えば(0)において $w$ を $w+\frac{1}{2}$ に、$x$ を $x+\frac{1}{2}$ に変えると、$w'$,$x'$ は変わらず $y'$ は $y'+\frac{1}{2}$ に、$z'$ は $z'+\frac{1}{2}$ に変わります。すると\begin{align}\vartheta_1\left(w+\frac{1}{2}\right)\vartheta_1\left(x+\frac{1}{2}\right)\vartheta_1(y)\vartheta_1(z) &=\vartheta_2(w)\vartheta_2(x)\vartheta_1(y)\vartheta_1(z)\\[1em] \vartheta_1(w')\vartheta_1(x')\vartheta_1\left(y'+\frac{1}{2}\right)\vartheta_1\left(z'+\frac{1}{2}\right) &=\vartheta_1(w')\vartheta_1(x')\vartheta_2(y')\vartheta_2(z')\end{align}つまり $w\to w+1/2$ , $x\to x+1/2$ なる変換によって $[1]\to [2211]$ , $[1]' \to [1122]'$ と変換されます。同様に
| 変換前 | $[1]$ | $[2]$ | $[3]$ | $[4]$ | $[1]'$ | $[2]'$ | $[3]'$ | $[4]'$ |
| 変換後 | $[2211]$ | $[1122]$ | $[4433]$ | $[3344]$ | $[1122]'$ | $[2211]'$ | $[3344]'$ | $[4433]'$ |
これらを例えば(5)に適用すると\begin{equation}[1122]+[2211]=[1122]'+[2211]'\tag{24}\end{equation}あるいは(9)に適用するなら\begin{equation}[2211]+[4433]=[2211]'+[4433]'\tag{25}\end{equation}(25)は対称性を考えて\begin{equation}[1122]+[3344]=[1122]'+[3344]'\tag{26}\end{equation}としてもちろん構いません(あるいは(10)から得る)。
(24)~(26)のような式からも色々な関係式をつくることができます。例として3倍公式をつくる課題を本ページ末においてます。
$w\to w+\frac{\tau}{2}$ , $x\to x+\frac{\tau}{2}$ なる変換ではどうなるでしょうか。このときは\begin{align}[1]&\rightarrow -q^{-\frac{1}{2}}e^{-\pi i(w+x)}[4411]\\ [2]&\rightarrow q^{-\frac{1}{2}}e^{-\pi i(w+x)}[3322]\\ [1]' &\rightarrow -q^{-\frac{1}{2}}e^{-\pi i(y'+z')}[1144]' \\ [2]' &\rightarrow q^{-\frac{1}{2}}e^{-\pi i(y'+z')}[2233]'\end{align}のように余計な因子がついてしまいます。しかし(0)より\begin{equation}y'+z'=w+x\tag{27}\end{equation}なので(5)に適用すると因子は消えます。\begin{equation}[3322]-[4411]=[2233]'-[1144]'\tag{28}\end{equation}また新たな式を得られました。
| 変換前 | $[1]$ | $[2]$ | $[3]$ | $[4]$ | $[1]'$ | $[2]'$ | $[3]'$ | $[4]'$ |
| 変換後 | $-\nu [4411]$ | $\nu [3322]$ | $\nu [2233]$ | $-\nu [1144]$ | $-\nu [1144]'$ | $\nu [2233]'$ | $\nu [3322]'$ | $-\nu [4411]'$ |
ただし $\nu=q^{-\frac{1}{2}}e^{-\pi i(w+x)}$ です。
(24)(25)(26)(28)はあくまで一部の例で、系1や系2において $w,x$ に半周期を足すという変換によって得られたものです。系1と系2の上位には定理0があります。なのでそもそも定理0に同じ変換をほどこしてもよかったですね。例えば\begin{equation}2\:[2211]=[1122]'+[2211]'-[3344]'+[4433]'\tag{29}\end{equation}あと全般的な注意として、(0)の一次変換を表す行列とその逆行列は全く同じなので、例えば(29)でダッシュ記号の有無を入れ替えてもOK:\begin{equation}2\:[2211]'=[1122]+[2211]-[3344]+[4433]\tag{30}\end{equation}
$w,x$ を $\frac{1+\tau}{2}$ 増加させる変換もありますが、省略します。
先ほど私たちは $w,x$ を $1/2$ 増加させたり $\tau/2$ を増加させたりしていました。要は2つの半周期を試したわけです。次はいっそ両方混ぜてみます。さらにいえば $\frac{1+\tau}{2}$ も混ぜちゃいましょう。\begin{equation}\begin{pmatrix}w\\x\\y\\z\end{pmatrix} \to\begin{pmatrix}w+\dfrac{1}{2}\\x+\dfrac{\tau}{2}\\y+\dfrac{1+\tau}{2}\\z\end{pmatrix}\tag{31}\end{equation}すると\begin{equation}\begin{pmatrix}w'\\x'\\y'\\z'\end{pmatrix} \to\begin{pmatrix}w'+\dfrac{\tau}{2}\\x'+\dfrac{1}{2}\\y'\\z'+\dfrac{1+\tau}{2}\end{pmatrix}\tag{32}\end{equation}となります。
このとき$$[3]\to iq^{-\frac{1}{2}}e^{-\pi i(x+y)}\:[4213]$$となります。また$$[1]'\to iq^{-\frac{1}{2}}e^{-\pi i(w'+z')}\:[4213]'$$となりますが、 $w'+z'=x+y$ より$$[1]'\to iq^{-\frac{1}{2}}e^{-\pi i(x+y)}\:[4213]'$$と書けます。このように計算したものを表にまとめましょう。$\a=iq^{-1/2}e^{-\pi i(x+y)}$ とおきます。
| 変換前 | $[1]$ | $[2]$ | $[3]$ | $[4]$ | $[1]'$ | $[2]'$ | $[3]'$ | $[4]'$ |
| 変換後 | $\a [2431]$ | $\a [1342]$ | $\a [4213]$ | $\a [3124]$ | $\a [4213]'$ | $\a [3124]'$ | $\a [2431]'$ | $\a [1342]'$ |
(3)式を再掲します。\begin{equation}2\:[3] =-[1]'+[2]'+[3]'+[4]'\tag{33}\end{equation}これに表3を適用すると\begin{equation}2\:[4213] =-[4213]'+[3124]'+[2431]'+[1342]'\tag{34}\end{equation}あるいは $w,x,y,z$ の対称性に注目して数字を入れ替えてもOK:\begin{equation}2\:[1234] =-[1234]'+[4321]'+[2143]'+[3412]'\tag{35}\end{equation}
(35)を真面目に書くとこうなります。\begin{align}&2\vartheta_1(w)\vartheta_2(x)\vartheta_3(y)\vartheta_4(z) \\[1em] &= -\vartheta_1\left(\frac{-w+x+y+z}{2}\right)\vartheta_2\left(\frac{w-x+y+z}{2}\right)\vartheta_3\left(\frac{w+x-y+z}{2}\right)\vartheta_4\left(\frac{w+x+y-z}{2}\right)\\&\quad +\vartheta_4\left(\frac{-w+x+y+z}{2}\right)\vartheta_3\left(\frac{w-x+y+z}{2}\right)\vartheta_2\left(\frac{w+x-y+z}{2}\right)\vartheta_1\left(\frac{w+x+y-z}{2}\right)\\&\quad +\vartheta_2\left(\frac{-w+x+y+z}{2}\right)\vartheta_1\left(\frac{w-x+y+z}{2}\right)\vartheta_4\left(\frac{w+x-y+z}{2}\right)\vartheta_3\left(\frac{w+x+y-z}{2}\right)\\&\quad +\vartheta_3\left(\frac{-w+x+y+z}{2}\right)\vartheta_4\left(\frac{w-x+y+z}{2}\right)\vartheta_1\left(\frac{w+x-y+z}{2}\right)\vartheta_2\left(\frac{w+x+y-z}{2}\right)\end{align}
系3の(18)(19)(21)を用いて\begin{align}&\bigl(\vartheta_4^{~2}\vartheta_1^{~3}(z)\vartheta_1(3z)+\vartheta_4^{~2}\vartheta_4^{~3}(z)\vartheta_4(3z)\bigr)^{2/3}\\&\quad\quad +\bigl(\vartheta_2^{~2}\vartheta_3^{~3}(z)\vartheta_3(3z)-\vartheta_2^{~2}\vartheta_4^{~3}(z)\vartheta_4(3z)\bigr)^{2/3}\\&\quad =\bigl(\vartheta_3^{~2}\vartheta_2^{~3}(z)\vartheta_2(3z)+\vartheta_3^{~2}\vartheta_4^{~3}(z)\vartheta_4(3z)\bigr)^{2/3}\end{align}を示せ。
以前に導出した式:$$\vartheta_4^{~2}\vartheta_4(z)^2+\vartheta_2^{~2}\vartheta_2(z)^2=\vartheta_3^{~2}\vartheta_3(z)^2$$を最後に使う。
$$[2211]+[3344]=[1122]'+[4433]'$$を示せ。
(7)を変換するとよい。
$$\vartheta_1^{~2}(z)\vartheta_2(z)\vartheta_2(3z)+\vartheta_2^{~2}(z)\vartheta_1(z)\vartheta_1(3z)=\vartheta_2\vartheta_1^{~2}(2z)\vartheta_2(2z)$$を示せ。
(24)を使って、3倍公式をつくるとよい(系3の導出を参考にする)。
加法定理の1つ\begin{align}\vartheta_1(z+y)\vartheta_2(z-y)\vartheta_3\vartheta_4 &= \vartheta_1(z)\vartheta_2(z)\vartheta_3(y)\vartheta_4(y)+\vartheta_3(z)\vartheta_4(z)\vartheta_1(y)\vartheta_2(y) \end{align}を示せ。
式(35)で $w\to z+y$ , $x\to z-y$ , $y\to 0$ , $z\to 0$ とすると $w'=-y$ , $x'=y$ , $y'=z$ , $z'=z$ となって示せる。
例4の式を別の方法で導こう。$$G(z):=\frac{a\vartheta_1(z)\vartheta_2(z)+b\vartheta_3(z)\vartheta_4(z)}{\vartheta_1(z+y)\vartheta_2(z-y)}$$を $z$ のみの関数とみる。$a,b$ は $z$ によらない定数であり、これを適切に定めることにより $G(z)$ が定数になることから例4の式を導出できる。
やり方は前々回と同じ。$G(z)$ は二重周期をもつことを確認できる。
$G(z)$ の分母をみると $z=-y$ , $z=y+\frac{1}{2}$ が $G(z)$ の極となる可能性があるが$$a=\frac{1}{\vartheta_1(y)\vartheta_2(y)}\;,\; b=\frac{1}{\vartheta_3(y)\vartheta_4(y)}$$と定めれば、分子の零点 $z=-y$ により一方の極は打ち消される。よって $G(z)$ は高々1位の極をもつ二重周期関数となるが、これは定数関数(ただし $y$ にはよる)に限る。
第5版です。いわずと知れた名著。楕円関数にかなりのページを割いています。

Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。