ばねの復元力を運動方程式に取り込もう。この微分方程式には三角関数が解として現れる。数学的に難しくなっていくけど、やることは今までと一緒だ。水平ばね振り子、鉛直ばね振り子、最後に空気抵抗がある場合も紹介。
ばねの復元力 $-kx(t)$ がある場合の運動方程式を解く．
ずっと運動方程式を解いてばかりいるけど、今日はバネの話をするよ。もちろん運動方程式だけどね！
復元力を考えるんだったな。のびと力が比例するというフックの法則だ。
フックの法則を簡単にするために、自然長のときの質点の位置を原点としようね。1次元の運動を考えよう。ばねの運動はどんな感じだった？
$x=A\sin\omega t$ が公式だった．「単振動」っていう運動だよな。等速円運動を真横から見た運動になるんだろう。
なんで？
・・・。
なんで単振動は円運動を横から見たのと同じ運動なの？
ぼーっと生きてたな。運動方程式を解いてみるよ。
ちょっと難しいけど大切だからがんばってほしいんだ！
以下のように座標を設定する．自然長を原点とすると位置と伸びは一致するので復元力は $-kx$ と書ける．$x>0$ ではばねは縮まろうとして $F<0$ ，$x<0$ なら伸びようとして $F>0$ となるから，負号がつくのを忘れないようにしよう．
また初期条件を $x(0)=0$ , $v(0)=v_0$ とする．
運動方程式は $ma(t)=-kx(t)$ なので\begin{equation}\frac{d^2x}{dt^2}=-\frac{k}{m}x(t)\tag{1}\end{equation}なる線型2階微分方程式を得る．
$x$ を2階微分するとまた $x$ が登場するが，係数が負となっているのに注目しよう．そんな関数は $\sin$ や $\cos$ だ．例えば $\sin ct$ を2回微分すると $-c^2\sin ct$ となる．$\sin$ の中身の係数が2回出てきているのが分かる．すなわちこの微分方程式の解は以下の２つが予想される.$$f(t)=\sin\sqrt{\frac{k}{m}}t\;,\; g(t)=\cos\sqrt{\frac{k}{m}}t $$実際に方程式に $f,g$ を代入するとちゃんと解になっている．つまり$$ \frac{d^2f}{dt^2}=-\frac{k}{m}f(t)$$ $$ \frac{d^2g}{dt^2}=-\frac{k}{m}g(t)$$ このとき $f,g$ を微分方程式の「特殊解」という．また，これらの特殊解を定数倍して足したもの（線型結合という）を$$x(t)=c_1f(t)+c_2f(t)$$ とおくと\begin{eqnarray*} \frac{d^2x}{dt^2} +\frac{k}{m}x(t)&=&c_1\left(\frac{d^2f}{dt^2} +\frac{k}{m}f(t) \right) + c_2\left(\frac{d^2g}{dt^2} +\frac{k}{m}g(t) \right) \\&=& c_1\cdot 0+c_2\cdot 0 \\&=& 0\end{eqnarray*}すなわち $x(t)$ も(1)の解だ．
$x(t)$ には２つの任意定数が入っている．線型2階微分方程式の解をすべて表現しようとすると必ず２つの任意定数が入ってくる．これを「一般解」という．あとは初期条件を代入して定数を決定すればよい．
すなわち微分方程式の一般解は$$x(t)=c_1 \sin\sqrt{\frac{k}{m}}t +c_2 \cos\sqrt{\frac{k}{m}}t $$初期条件 $x(0)=0$ より $c_2=0$ なので $$x(t)=c_1 \sin\sqrt{\frac{k}{m}}t $$微分すれば$$v(t)= c_1 \sqrt{\frac{k}{m}} \cos\sqrt{\frac{k}{m}}t $$ となるので初期条件 $v(0)=v_0$ を代入すると $c_1=v_0\sqrt{m/k}$ $$\therefore\quad x(t)=v_0\sqrt{\frac{m}{k}}\sin \sqrt{\frac{k}{m}}t $$
急に難しくなったぞ！
ばねだけのときはサインとコサインを両方解にぶちこむんだ。
ちなみに $\sin$ の中の $\sqrt{\frac{k}{m}} $ を角速度（角振動数）といって $\omega$ とすることが多いよ。すると解は $A\sin\omega t$ の形になるね。
微分方程式はちょっと状況が変わると難易度がぐんと上がるから，たくさん練習しておく必要があるんだ。物理を極めるなら数学の職人技が必須なのさ。
三角関数が解になるのは分かったけど，何か天下り的だったな．自力でゴリゴリ求めるのは無理なの？
面倒だしやる必要はないと思うけど，ちゃんと方法あるよ．最後の「補足」の節で紹介するね．
ぼくから練習問題を出すよ！ばねのタイプの微分方程式に慣れよう。
$$\frac{d^2x}{dt^2}+4x=0$$の一般解を求め，初期条件 $x(0)=0$ , $x(\frac{\pi}{4})=3$ としたときの解を求めよ．
予想される特殊解は $\sin2t$ と $\cos2t$ である．試しに代入すると題意の方程式を満たす．よって一般解は$$x=c_1\sin 2t+c_2\cos 2t$$初期条件により $c_2=0$ および $c_1=3$$$\therefore\quad x=3\sin 2t$$
特殊解の予想が難しかったら，$x=\sin\omega t$ をとりあえず代入してみて！すると $\omega$ が求まるよ。
$$\frac{d^2x}{dt^2}+6x=0$$の一般解を求めよ．角振動数 $\omega$ はいくらか．
一般解は $ x=c_1\sin \sqrt{6}t+c_2\cos \sqrt{6}t$ ．$\omega=\sqrt{6}$
次は上下に振動する場合をやるんだ。水平と何が違う？
まったく同じ単振動をするんだけど、振動中心が自然長の位置よりも下にあるんだよな。これも微分方程式で導くってことだね。
もちろんさ！まぁ水平ばね振り子の結果を使って座標を平行移動するって方法でも片付けられるんだけどね。先に力技で解く方法、次にスマートな方法を紹介するよ！
先ほどと全く同じ座標をとる．
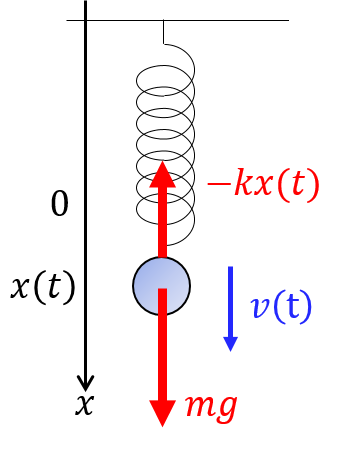
かかる力は $F=mg-kx$ なので運動方程式は\begin{equation}\frac{d^2x}{dt^2}+\frac{k}{m}x=g\tag{2}\end{equation}右辺がゼロでないのが先ほどとの違いである．このように右辺に邪魔者があるものを「非斉次方程式」といい，解法が複雑になりやすいが今は定数なのでやりやすい．$x$ に定数 $C$ を代入してみると $$C=\frac{mg}{k}$$となる．水平ばね振り子のときの一般解にこの定数を加えたものが(2)の一般解となる．$$\therefore\quad x(t)=c_1 \sin\sqrt{\frac{k}{m}}t +c_2 \cos\sqrt{\frac{k}{m}}t+ \frac{mg}{k} $$実際に代入して解であることを確かめてほしい．
定数を加えるとかなかなか思いつかないと思うんだけど。
微分方程式のパターンをある程度知っている前提かもしれないね。右辺がゼロのときの解が(1)で分かっているときは，それにさらに何かを加えるというのは常套手段なんだ。
ここで得られた解は $x=mg/k$ を中心とした単振動だな。簡単のために $\cos$ の項をなくしたら分かりやすい。
実際 $X=x-mg/k$ と変換すると $$X(t)= c_1 \sin\sqrt{\frac{k}{m}}t +c_2 \cos\sqrt{\frac{k}{m}} $$となってふつうの単振動である．$x=mg/k$ を原点とした座標 $X(t)$ をとると式がより見やすくなるわけである．
振動中心がずれることを知っているなら次のように解くと楽だよ。
かかる力は $F=mg-kx$ である．ここで$$x_0=\frac{mg}{k}$$とおくと $F=-k(x-x_0)$ となる．すなわち運動方程式は$$\frac{d^2x}{dt}=-\frac{k}{m} (x-x_0) $$ここで $X(t)=x(t)-x_0$ と変換（平行移動）する．$x_0$ は定数なので$$\frac{dX}{dt}=\frac{dx}{dt}$$$$ \frac{d^2X}{dt}= \frac{d^2x}{dt}$$が成立する．従って運動方程式は $$\frac{d^2X}{dt}=-\frac{k}{m}X(t)$$と書き直せる．これは単振動の形をしているから$$ X(t)= c_1 \sin\sqrt{\frac{k}{m}}t +c_2 \cos\sqrt{\frac{k}{m}} $$という一般解が得られる．座標をもとに戻すと$x=X+x_0$ より$$ x(t)=c_1 \sin\sqrt{\frac{k}{m}}t +c_2 \cos\sqrt{\frac{k}{m}}t+ \frac{mg}{k} $$
こんな風にね。この問題では振動中心がずれて復元力が $F=-k(x-x_0)$ と書けることを知っていると簡単に思いつくんだ。逆に物理現象をまったく見ずに純粋に数学だけでやると，方程式を解くのがしんどかったりするんだ。
この講座は基本的になるべく数学的処理で進めていくけど，高校で学んだ知識をバランスよく動員してゴールを思い描きながら計算していこうね。
ぼくから応用問題を出すよ！結構むずかしいから、微分方程式を既習の人向けなんだ。解法をしっかり学びたいときは常微分方程式シリーズD5の後半「[2]定数係数の方程式」を見てね。リンクはこっちだよ！
【D5】斉次2階線型微分方程式
水平ばね振り子を考える．ばね定数 $m\omega^2$ とする．空気抵抗力が速さに比例して $-2m\gamma v$ と書けるとき，運動方程式を解け．初期条件を $x(0)=0$ , $v(0)=v_0$ とする．
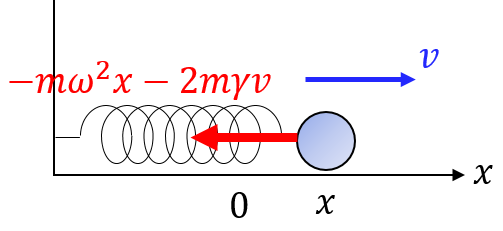
運動方程式は\begin{equation}\frac{d^2x}{dt^2}+2\gamma\frac{dx}{dt}+\omega^2x=0\tag{3}\end{equation}ここで方程式 $\lambda^2+2\gamma\lambda+\omega^2=0$ の２解 $ \lambda_1$ , $\lambda_2$ を用いて特殊解は$e^{\lambda_1t}$ , $e^{\lambda_2t}$ と書ける（実際(3)に試行解 $x=e^{\lambda t}$ を代入してみよう）．
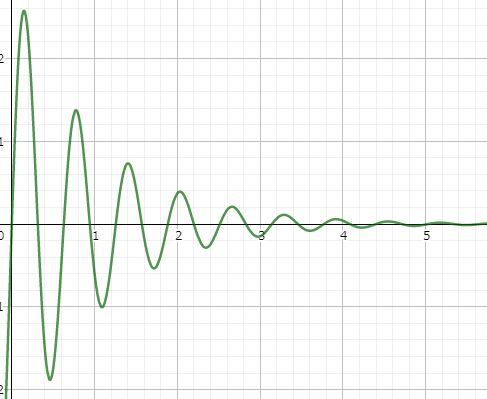
よって一般解はそれらの線型結合であるから$$x(t)=Ae^{(-\gamma+\sqrt{\gamma^2-\omega^2})t}+B e^{(-\gamma-\sqrt{\gamma^2-\omega^2})t}$$初期条件 $x(0)=0$ から $B=-A$ である．よって$$ x(t)=Ae^{-\gamma t}\left(e^{\sqrt{\gamma^2-\omega^2}t}-e^{-\sqrt{\gamma^2-\omega^2}t}\right)$$ 微分すると $$v(t)=A \sqrt{\gamma^2-\omega^2} e^{-\gamma t}\left(e^{\sqrt{\gamma^2-\omega^2}t}+e^{-\sqrt{\gamma^2-\omega^2}t}\right) $$初期条件 $v(0)=v_0$ より$$A=\frac{v_0}{2 \sqrt{\gamma^2-\omega^2} }$$\begin{equation}\therefore\quad x(t)= \frac{v_0}{2 \sqrt{\gamma^2-\omega^2} } e^{-\gamma t}\left(e^{\sqrt{\gamma^2-\omega^2}t}-e^{-\sqrt{\gamma^2-\omega^2}t}\right)\tag{4}\end{equation} これで形としては解けたが，根号が負である可能性を考慮して場合分けする．実際，空気抵抗は弾性力に比べてはるかに小さいだろうから $\gamma<\omega$ であり根号内は負であると考えられる．$\gamma<\omega$ なら根号を $i\sqrt{\omega^2-\gamma^2}$ と書き直す．
- $\gamma>\omega$ の場合((4)のままでもOK)$$x(t)=\frac{v_0}{\sqrt{\gamma^2-\omega^2} } e^{-\gamma t}\sinh\sqrt{\gamma^2-\omega^2}t$$
- $\omega>\gamma$ の場合$$x(t)=\frac{v_0}{ \sqrt{\omega^2-\gamma^2} } e^{-\gamma t}\sin\sqrt{\omega^2-\gamma^2}t$$
普通は後者の解が妥当だよ。$\sin$ があるから振動するんだけど，その振幅は $e^{-\gamma t}$ によってどんどん減っていくんだ。こういうのを減衰振動っていうよ！
単振動の方程式の解を自力で求める方法があるよ！簡単のために $m=k=1$ としておくね．
単振動の式$$\frac{d^2x}{dt^2}=-x$$の両辺に $\dfrac{dx}{dt}$ をかけます．$$\frac{dx}{dt}\frac{d^2x}{dt^2}=-x \dfrac{dx}{dt}$$$$\therefore\quad\frac{d}{dt}\left[\frac{1}{2}\left(\frac{dx}{dt}\right)^2\right]=\frac{d}{dt}\left(-\frac{1}{2}x^2\right)$$両辺を積分して$$\left(\frac{dx}{dt}\right)^2=-x^2+C$$平方根をとり$$\pm\frac{dx}{dt}=\sqrt{C-x^2}$$ 初期条件 $x(0)=0$ , $v(0)=v_0>0$ とすると $C=v_0^2$ と定まります．$$\therefore\quad \frac{dx}{dt}=\sqrt{v_0^2-x^2}$$変数分離して$$\frac{dx}{\sqrt{v_0^2-x^2}}=dt$$$x(0)=0$ に注意して積分をとります．$$\int_0^x\frac{dx}{\sqrt{v_0^2-x^2}}=\int_0^tdt$$積分を実行して$$\arcsin\frac{x}{v_0}=t$$$$\therefore\quad x=v_0\sin t$$と，やはり $x(t)$ はサインで表されることが分かりました．
微積分と高校物理シリーズ
【H1】力学の表現と本シリーズの意義
【H2】力がゼロの運動方程式と等速直線運動
【H3】落体運動の法則はただ１つ
【H4】ばねの微分方程式 水平・鉛直・空気抵抗
【H5】等速・非等速円運動と微分方程式
【H6】ベクトルの極座標成分
【H7】単振り子の方程式と厳密解
Please support me!
記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。
