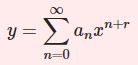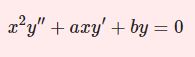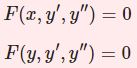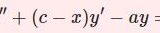多様な例題あり。級数解の例として超幾何微分方程式の解き方を解説する。点0で正則でないためフロベニウス法を使う。これにより現れる特殊解はガウスの超幾何関数とよばれ、ポッホハマー記号を使うと記述しやすい。
級数法・フロベニウス法については
を参照。
\begin{equation}x(1-x)y^{\prime\prime}+[c-(a+b+1)x]y'-aby=0\tag{1}\end{equation}
この方程式は $x=0$ で正則でないため、フロベニウス法を使います。さんざんこれまでやってきましたが，解法の流れは
これにより級数の形が２つ決まる。
$y=\sum_{n=0}^\infty a_nx^{n+r}$ $(a_0\neq 0)$を超幾何微分方程式(1)に代入すると$$r(r+c-1)a_0x^{r-1}+ \sum_{n=0}^\infty\bigl[(n+r+1)(n+r+c)a_{n+1}-(n+r+a)(n+r+b)a_n\bigr]x^{n+r}$$よって第1項から決定方程式 $r(r+c-1)=0$ を得ます．よって$$r=0,1-c$$それぞれの $r$ について級数解が得られます．その級数解は特殊解なわけですから線型結合して(1)の一般解を得るわけです．
$r=0$ のときは級数解を$$y=\sum^\infty_{n=0}a_nx^n \; \; , \; a_0\ne 0$$とおいて微分方程式(1)に代入し $x$ に関して恒等的に成り立つことにより以下の関係式を得ます．$$\begin{cases}a_1=\displaystyle\frac{ab}{c}a_0\\a_{n+1}=\dfrac{(n+a)(n+b)}{(n+c)(n+1)}a_n \;\;(n\geq 1)\end{cases}$$1番目の式は2番目の式に含めることができて結局$$a_{n+1}=\displaystyle\frac{(n+a)(n+b)}{(n+c)(n+1)}a_n \;\;(n\geq 0)$$という漸化式が導かれます．これより一般項は$$a_n=\frac{(a)_n(b)_n}{(c)_nn!}a_0$$となります．なお $(x)_n$ はポッホハマー記号といい$$(x)_n=x(x+1)(x+2)\cdots(x+n-1)$$で定義されます．ただし $(x)_0=1$ とします．
よって $a_0=1$とした特殊解は以下で定義されるガウスの超幾何函数
$$F(a,b,c;x)\equiv \sum^\infty_{n=0}\frac{(a)_n(b)_n}{(c)_nn!}x^n$$ であらわされることが分かります。なので1つ目の特殊解は
$$y_1(x)=F(a,b,c;x)$$
$r=1-c$ のときは級数解を$$y=\sum^\infty_{n=0}a_nx^{n+1-c} \; \; , \; a_0\ne 0$$とおいて微分方程式(1)に代入します。計算すると漸化式は $$a_{n+1}=\frac{(n+a-c+1)(n+b-c+1)}{(n+2-c)(n+1)}a_n \;\;(n\geq 0)$$漸化式を繰り返し用いて$$a_n=\frac{(a-c+1)_n(b-c+1)_n}{(2-c)_nn!}$$なので級数は$$\sum^\infty_{n=0} \frac{(a-c+1)_n(b-c+1)_n}{(2-c)_nn!} x^{n+1-c} $$よって $a_0=1$ として２つめの特殊解
$$y_2(x)=x^{1-c}F(a-c+1,b-c+1,2-c;x)$$
を得ます．
※超幾何微分方程式の特殊解に関する詳細な理論は以下を参照：
これで２つの特殊解が求まったので一般解は$$y=c_1F(a,b,c;x)+c_2x^{1-c}F(a-c+1,b-c+1,2-c;x)$$となります． $c$ の値によっては２つの特殊解が独立でないときもあります．そのときはここで導出した方法で一般解が与えられません．
超幾何関数は一見みたこともないような関数に見えますが，実際はよく知られた関数に書き直せる場合も多いです。例えば$$\arcsin x=xF\left(\frac{1}{2},\frac{1}{2},\frac{3}{2};x^2\right)$$などです．微分方程式の解が超幾何関数で表せたところで終わるのではなく，初等関数で表せないか考えるようにしましょう．
$8x(1-x)y^{\prime\prime}+(4-14x)y'-y=0$ を解け．
変形すると\begin{equation}x(1-x)y^{\prime\prime}+\left(\frac{1}{2}-\frac{7}{4}x\right)y'-\frac{1}{8}y=0\end{equation}これは(1)と見比べると$$c=\frac{1}{2}\;,\;a+b+1=\frac{7}{4}\;,\;ab=\frac{1}{8}$$これにより $a=1/2\;,\;b=1/4\;,\;c=1/2$ ですので1つ目の特殊解は\begin{eqnarray*}y_1&=&F\left(\frac{1}{2},\frac{1}{4},\frac{1}{2},x\right)\\&=& \sum_{n=0}^\infty\frac{(1/2)_n(1/4)_n}{(1/2)_n}\frac{x^n}{n!}\\&=&\sum_{n=0}^\infty\left(\frac{1}{4}\right)_n\frac{x^n}{n!}\\&=&\sum_{n=0}^\infty\frac{1}{4}\left(\frac{1}{4}+1\right)\cdots\left(\frac{1}{4}+n-1\right)\frac{x^n}{n!}\\&=&(1-x)^{-\frac{1}{4}}\end{eqnarray*}最後の等式は $(1-x)^{-\frac{1}{4}}$ をマクローリン展開することで確認できます．
もう１つの特殊解は
\begin{eqnarray*}y_2&=&x^{1-c}F(a-c+1,b-c+1,2-c;x)\\&=&\sqrt{x}F\left(1,\frac{3}{4},\frac{3}{2};x\right)\end{eqnarray*}これより先は計算できませんでした．実際できるのでしょうか・・・？$y_1$ が分かっているので $y_2=y_1u(x)$ と置いてみる価値はあるかもしれません．でもwolfram使っても解が出てこないのできっと無駄に終わると思い，ヤメにします．初等関数等であらわせた方いたら教えてください．
というわけで一般解は$$y=c_1(1-x)^{-\frac{1}{4}}+c_2\sqrt{x}F\left(1,\frac{3}{4},\frac{3}{2};x\right)$$
$x(1-x)y^{\prime\prime}+(3-5x)y'-4y=0$ を解け．
$$a=b=2\;,\;c=3$$1つ目の特殊解は\begin{eqnarray*}y_{1'}&=&F(2,2,3;x)\\&=&\sum_{n=0}^\infty\frac{(2)_n(2)_n}{(3)_n}\frac{x^n}{n!}\\&=&\sum_{n=0}^\infty\frac{(n+1)!(n+1)!\cdot 2}{(n+2)!}\frac{x^n}{n!}\\&=& 2\sum_{n=0}^\infty\frac{n+1}{n+2}x^n\\&=& 2\sum_{n=0}^\infty \left(1-\frac{1}{n+2}\right)x^n\\&=& 2(1+x+x^2+\cdots )-2\left(\frac{1}{2}+\frac{x}{3}+\frac{x^2}{4}+\cdots\right)\\&=& \frac{2}{1-x}-\frac{2}{x^2}\left(\frac{x^2}{2}+\frac{x^3}{3}+\frac{x^4}{4}+\cdots\right)\\&=& \frac{2}{1-x}+\frac{2}{x^2}\{x+\log(1-x)\}\end{eqnarray*}定数$2$は割っておいて
$$y_1=\frac{1}{x(1-x)}+\frac{\log(1-x)}{x^2}$$
もう1つの特殊解は\begin{eqnarray*}y_2&=&x^{1-c}F(a-c+1,b-c+1,2-c;x)\\&=&\frac{1}{x^2}F(0,0,-1;x)\\&=& \frac{1}{x^2}\sum_{n=0}^\infty \frac{(0)_n(0)_n}{(-1)_n}\frac{x^n}{n!}\\&=&\frac{1}{x^2}\end{eqnarray*}となります．しかし $n=2$ とかでは発散してしまうのでは，いや分子がゼロだからいいのか？何なのか．超幾何関数を公式のまま使っても自信が持てず，原点に帰る必要があります(※ Wolframによると $F(0,0,-1;x)=1$ とのことですので合ってる)．
$y=\sum_{n=0}^\infty a_nx^{n+r}$ を方程式に代入すると最低次の項について等式 $r(r+2)a_0=0$ を得ます（決定方程式）．よって $r=0,-2$ となります．$r=0$ を選ぶと上で得た特殊解 $y_1$ が現れますのでこちらはもういいでしょう．
$r=-2$ とすると $y=\sum_{n=0}^\infty a_nx^{n-2}$ を微分方程式に代入し，割と面倒な計算を経て以下の漸化式を得ます．$$\begin{cases}a_0 &=& 任意\\a_1&=&0\\a_2&=& 任意\\a_n&=&\displaystyle\frac{(n-1)^2}{n(n-2)}a_{n-1}\;(n\ge 3)\end{cases}$$よって一般項は$$\begin{cases}a_0 &=& 任意\\a_1&=&0\\a_2&=& 任意\\a_n&=&\displaystyle\frac{(n-1)!(n-1)!}{(3)_{n-2}(n-2)!}a_2\;(n\ge 2)\end{cases}$$以上から特殊解 $y_2$ は \begin{eqnarray*}y_2&=&a_nx^{n-2}\\&=&\frac{a_0}{x^2}+a_2\sum_{n=2}^\infty\frac{(n-1)!(n-1)!}{(3)_{n-2}(n-2)!}x^{n-2}\\&=& \frac{a_0}{x^2}+a_2\sum_{n=0}^\infty\frac{(2)_n(2)_n}{(3)_n}\frac{x^n}{n!}\\&=& \frac{a_0}{x^2}+a_2F(2,2,3;x)\end{eqnarray*}第2項はまさに1つ目の特殊解 $y_1$ です．あとで線型結合するので $a_2=0$ として無視しておきます．すると$$y_2=\frac{1}{x^2}$$と特殊解が出ました！結局さっきので合ってましたね．以上より一般解は$$y=c_1\left(\frac{1}{x(1-x)}+\frac{\log(1-x)}{x^2}\right)+\frac{c_2}{x^2}$$
超幾何微分方程式(1)において $c$ が負整数の場合は注意が必要なのかもしれません．
$x(1-x)y^{\prime\prime}+\displaystyle\frac{1}{4}y'+2y=0$ を解け．
式(1)と比べることにより$$a=-2\;,\;b=1\;,\;c=\frac{1}{4}$$1つ目の特殊解は\begin{eqnarray*}y_{1}&=&F(-2,1,1/4;x)\\&=&\sum_{n=0}^\infty\frac{(-2)_nn!}{(1/4)_n}\frac{x^n}{n!}\\&=&\sum_{n=0}^\infty\frac{(-2)_n}{(1/4)_n}x^n\\&=&1-8x+\frac{32}{5}x^2\end{eqnarray*}このように $a$ や $b$ が負整数の場合は，ある $n$ で分子に $0$ が現れ，級数は打ち切りになります．よって多項式になるのです．
2つ目の特殊解は\begin{eqnarray*}y_{2}&=& x^{\frac{3}{4}}F\left(-\frac{5}{4},\frac{7}{4},\frac{7}{4};x\right)\\ &=& x^{\frac{3}{4}}\sum_{n=0}^\infty\frac{(-5/4)_n}{n!}x^n\\ &=& x^{\frac{3}{4}}(1-x)^{\frac{5}{4}}\end{eqnarray*}よって一般解は$$y=c_1(32x^2-40x+5)+c_2 x^{\frac{3}{4}}(1-x)^{\frac{5}{4}}$$
以上３つの例題を見てきました．超幾何微分方程式の解は無限級数で表される超幾何関数です．そしてその超幾何関数は非常に多くの初等関数を含んでいることが本記事で分かっていただけたのではないでしょうか．
超幾何関数には様々な変換公式があります。こちらを参照：
$f(z)=(1+z)^n$ および $g(z)=\ln(1-z)$ を超幾何級数で表せ。
マクローリン展開してみましょう。$f(z)$ は二項定理で$$f(z)=\sum_{r=0}^\infty n(n-1)\cdots(n-r+1)\frac{z^r}{r!}$$無限級数に見えますが、$r>n$ の項においては積の因数のどれかがゼロとなりますので、実質は $r\ge n$ までの有限和です。変形して$$f(z)=\sum_{r=0}^\infty \frac{(-n)_r(-z)^r}{r!}$$任意の数 $a$ によって$$f(z)=\sum_{r=0}^\infty \frac{(-n)_r(a)_r}{(a)_r}\frac{(-z)^r}{r!}$$$$\therefore \quad f(z)=F(-n,a,a;-z)$$一方$$g(z)=-\sum_{n=1}^\infty\frac{z^n}{n}=-z\sum_{n=0}^\infty\frac{z^n}{n+1}$$うまく超幾何級数の形にもっていきます。$$g(z)=-z\sum_{n=0}^\infty\frac{(1)_n }{(2)_n}z^n=-z\sum_{n=0}^\infty\frac{(1)_n (1)_n }{(2)_n}\frac{z^n}{n!}$$$$\therefore\quad g(z)=-zF(1,1,2;z)$$
Show that $$\frac{d}{dz}F(a,b,c;z)=\frac{ab}{c}F(a+1,b+1,c+1;z)$$
$$\frac{d}{dz}F(a,b,c;z)=\sum_{n=1}^\infty\frac{(a)_n(b)_n}{(c)_n}\frac{z^{n-1}}{(n-1)!}$$添え字をずらして$$\frac{d}{dz}F(a,b,c;z)=\sum_{n=0}^\infty\frac{(a)_{n+1}(b)_{n+1}}{(c)_{n+1}}\frac{z^{n}}{n!}$$$(a)_{n+1}=a\cdot (a+1)_n$ となることを利用して$$\frac{d}{dz}F(a,b,c;z)=\frac{ab}{c}\sum_{n=0}^\infty\frac{(a+1)_{n}(b+1)_{n}}{(c+1)_{n}}\frac{z^{n}}{n!}$$よって示されました。
Show that \begin{eqnarray*}&&c[c-1-(2c-a-b-1)x]F(a,b,c;x)+(c-a)(c-b)xF(a,b,c+1;x)\\&&\quad =c(c-1)(1-x)F(a,b,c-1;x)\end{eqnarray*}
\begin{eqnarray*}LHS &=& c(c-1)F(a,b,c;x)-c(2c-a-b-1)\sum_{n=0}^\infty\frac{(a)_n (b)_n}{(c)_n}\frac{x^{n+1}}{n!}\\&&+(c-a)(c-b)\sum_{n=0}^\infty\frac{(a)_n(b)_n}{(c+1)_n}\frac{x^{n+1}}{n!}\\ &=& c(c-1)F(a,b,c;x)-c(c-1)x\sum_{n=0}^\infty\frac{(a)_n (b)_n}{(c-1)_{n+1}}(2c-a-b-1)\frac{x^n}{n!}\\&&+c(c-1)x\sum_{n=0}^\infty\frac{(a)_n(b)_n}{(c-1)_{n+2}}(c-a)(c-b)\frac{x^n}{n!} \end{eqnarray*}２つのシグマをまとめます。\begin{eqnarray*}&=& c(c-1)F(a,b,c;x)\\&&-c(c-1)x\sum_{n=0}^\infty\left[\frac{(a)_n (b)_n}{(c-1)_{n+1}}(2c-a-b-1)-\frac{(a)_n(b)_n}{(c-1)_{n+2}}(c-a)(c-b)\right]\frac{x^n}{n!}\\&=& c(c-1)F(a,b,c;x)\\&&+c(c-1)x\sum_{n=0}^\infty\frac{(a)_n (b)_nx^n}{(c-1)_nn!}\frac{-c^2+ab+c-2cn+an+bn+n}{(c+n-1)(c+n)}\end{eqnarray*}第1項だけ取り出して変形すると\begin{eqnarray*}F(a,b,c;x)&=&\sum_{n=0}^\infty\frac{(a)_n(b)_n}{(c-1)_n}\frac{c-1}{c+n-1}\frac{x^n}{n!}\\ &=& \sum_{n=0}^\infty\frac{(a)_n(b)_n}{(c-1)_n}\left(1-\frac{n}{c+n-1}\right)\frac{x^n}{n!}\\ &=& F(a,b,c-1;x)-\sum_{n=0}^\infty\frac{(a)_n(b)_n}{(c-1)_n}\frac{n}{c+n-1}\frac{x^n}{n!}\\ &=& F(a,b,c-1;x)-\sum_{n=1}^\infty\frac{(a)_n(b)_n}{(c-1)_n}\frac{1}{c+n-1}\frac{x^n}{(n-1)!}\end{eqnarray*}添え字をずらして\begin{eqnarray*}F(a,b,c;x) &=& F(a,b,c-1;x)-x\sum_{n=0}^\infty\frac{(a)_{n+1}(b)_{n+1}}{(c-1)_{n+1}}\frac{1}{c+n}\frac{x^n}{n!} \\ &=& F(a,b,c-1;x)-x\sum_{n=0}^\infty\frac{(a)_n(b)_nx^n}{(c-1)_nn!}\frac{(a+n)(b+n)}{(c+n)(c+n-1)}\end{eqnarray*}したがって与式の左辺は\begin{eqnarray*}LHS &=& c(c-1)\left(F(a,b,c-1;x)-x\sum_{n=0}^\infty\frac{(a)_n(b)_nx^n}{(c-1)_nn!}\frac{(a+n)(b+n)}{(c+n)(c+n-1)}\right)\\&&+c(c-1)x\sum_{n=0}^\infty\frac{(a)_n (b)_nx^n}{(c-1)_nn!}\frac{-c^2+ab+c-2cn+an+bn+n}{(c+n-1)(c+n)}\\ &=& c(c-1)F(a,b,c-1;x)-c(c-1)x\sum_{n=0}^\infty\frac{(a)_n(b)_nx^n}{(c-1)_nn!}\\ &=&c(c-1)(1-x)F(a,b,c-1;x)\end{eqnarray*}
次の記事：
本記事では、下記の本を大いに参考にしています。厳密性はほどほどに、なるべくたくさんの演習問題が用意されています。産業や自然界における事例も豊富。数学科以外の理学部・工学部生にオススメです。
【Amazon】常微分方程式 (技術者のための高等数学)
常微分方程式シリーズ
Please support me!
記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。
