微分幾何学の講座・第12回。空間曲線のお話です。第3回では空間曲線の動標構の1つであるフレネフレームの解説をしました。今回は曲面の存在を前提として、それに乗っかった曲線を調べるためのダルブーフレームを導入します。そしてそのフレームから得られる新たな量「測地的曲率」「測地的捩率」を見ていきましょう。

一般相対論を学ぶのにも役立ちそう!

曲面にいる立場からすると、フレネフレームよりも便利な標構があるよ!
シリーズを通して読むとベターです。
前回はこちら:
過去記事で学んだように、パラメータ表示された曲線に沿って変化する「動く座標系」のようなものを動標構といい、特にフレネ標構(フレーム)を導入しました。
弧長パラメータ表示された曲線 $\bm{C}(s)$ におけるフレネフレームは以下で定める単位接ベクトル $\bm{e}_1(s)$、単位主法線ベクトル $\bm{e}_2(s)$、単位従法線ベクトル $\bm{e}_3(s)$ の組である。\begin{eqnarray}\bm{e}_1(s)&:=&\bm{C}'(s)\tag{1} \\ \bm{e}_2(s) &:=& \frac{\bm{C}''(s)}{|\bm{C}''(s)|}\tag{2} \\ \bm{e}_3(s)&:=&\bm{e}_1(s)\times \bm{e}_2(s)\tag{3}\end{eqnarray}
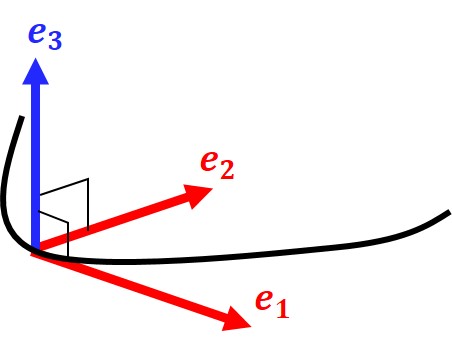
3つの単位ベクトルは正規直交基底をなすのでした。これをもとに曲率と捩率が定義されました。
\begin{equation}\kappa(s)=\bm{e}_1'(s)\cdot \bm{e}_2(s)\tag{4}\end{equation}
\begin{equation}\tau(s)=\bm{e}_2'(s)\cdot \bm{e}_3(s)\tag{5}\end{equation}
あるいは\begin{equation}\kappa(s)=|\bm{C}''(s)|\;,\;\tau(s)=\frac{\mathrm{det}\left(\bm{C}'(s),\bm{C}''(s),\bm{C}'''(s)\right)}{|\bm{C}''(s)|^2}\tag{6}\end{equation}とも書けます。また $\bm{C}''(s)=\kappa(s)\bm{e}_2(s)$ を曲率ベクトルとよびます。
さらにフレネフレームの変化は、それ自身の係数を曲率と捩率で表せて
\begin{equation}\frac{d}{ds}\begin{pmatrix}\bm{e}_1(s)\\\bm{e}_2(s)\\\bm{e}_3(s)\end{pmatrix}=\begin{pmatrix}0 & \kappa(s) & 0\\-\kappa(s) & 0 & \tau(s)\\0 & -\tau(s) & 0\end{pmatrix}\begin{pmatrix}\bm{e}_1(s)\\\bm{e}_2(s)\\\bm{e}_3(s)\end{pmatrix}\tag{7}\end{equation}
となるのでした。
今日の記事では、これとは違った動標構の紹介をします。
2つのパラメータ $u,v$ で表される曲面$$\bm{S}(u,v)=\bigl(x(u,v),y(u,v),z(u,v)\bigr)$$は、$uv$ 平面上の領域 $D$ を3次元空間に写したものです。そして以前に見たように $D$ に含まれる曲線 $(u(s),v(s))$ はこの曲面上の曲線に写されます。\begin{equation}\bm{C}(s):=\bm{S}\bigl(u(s),v(s)\bigr)\tag{8}\end{equation}$\bm{C}(s)$ は弧長パラメータ表示されているとしましょう。
ちなみに曲面上の点 $\bm{S}(u,v)$ における、曲面の単位法ベクトルはこちらで見たように\begin{equation}\bm{n}(u,v):=\frac{\bm{S}_u\times\bm{S}_v}{|\bm{S}_u\times\bm{S}_v|}\tag{9}\end{equation}と定義されるのでした。
この曲線についてダルブーフレームという動標構を定めます。フレネフレームでは曲面の存在を前提としませんでしたが、ダルブーフレームでは、曲面がまずあって、その上に乗っかる曲線について標構を定めるのです。
弧長パラメータ表示された曲面上の曲線 $\bm{C}(s):=\bm{S}\bigl(u(s),v(s)\bigr)$ におけるダルブーフレームは以下で定める3つの単位ベクトルの組である。\begin{eqnarray}\bm{d}_1(s)&:=& \bm{C}'(s)\tag{10} \\ \bm{d}_3(s) &:=& \bm{n}\bigl(u(s),v(s)\bigr)\tag{11} \\ \bm{d}_2(s)&:=&\bm{d}_3(s)\times \bm{d}_1(s)\tag{12}\end{eqnarray}
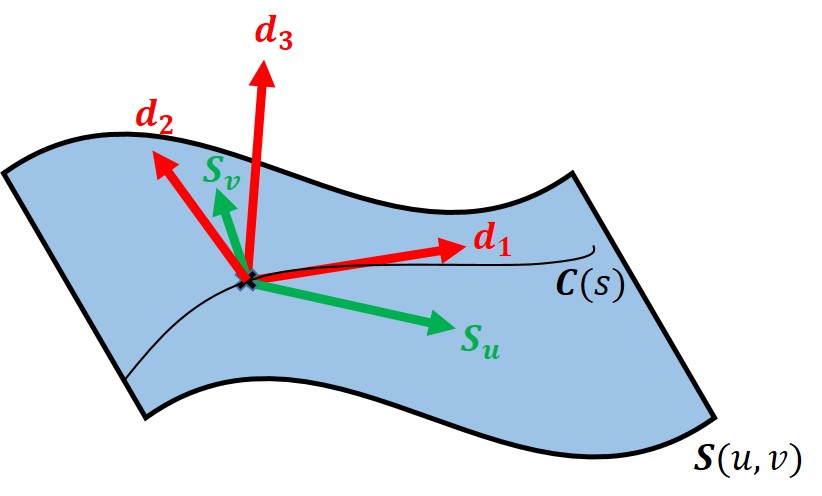
明らかに $\bm{d}_1=\bm{e}_1$ です。つまりダルブーフレームでもフレネフレームでも、単位接ベクトルを1つめの基底とするのは同じです。次に $\bm{d}_3$ を、曲線が乗っかっている曲面の法ベクトルで定義する…ここがフレネフレームとの大きな違いです。$$\bm{d}_1(s)=\bm{S}_u u'+\bm{S}_v v'$$より $\bm{d}_1$ は曲面の接ベクトルが張る面にあるため、明らかに $\bm{d}_3$ に直交します。あとは $\bm{d_1},\bm{d_2},\bm{d_3}$ が右手系に直交するように $\bm{d}_2$ を(12)で定義しています。$\bm{d}_1$ と $\bm{d}_2$ は曲面の法ベクトルと直交するため、曲面の接平面に含まれます。
2つの動標構の共通点は接ベクトル $\bm{d}_1=\bm{e}_1$ であり、ともに右手系で定めていることから、$\bm{d}_1$ を軸として $\bm{e}_2$ , $\bm{e}_3$ を回転させると、$\bm{d}_2$ , $\bm{d}_3$ と一致します。すなわち $s$ に応じた角度 $\t(s)$ があって\begin{equation}\begin{pmatrix}\bm{d}_1 \\ \bm{d}_2 \\ \bm{d}_3\end{pmatrix}= \begin{pmatrix} 1 & 0 & 0 \\ 0 & \cos\t(s) & -\sin\t(s) \\ 0 & \sin\t(s) & \cos\t(s)\end{pmatrix}\begin{pmatrix} \bm{e}_1 \\ \bm{e}_2 \\ \bm{e}_3\end{pmatrix}\tag{13}\end{equation}逆変換は\begin{equation}\begin{pmatrix}\bm{e}_1 \\ \bm{e}_2 \\ \bm{e}_3\end{pmatrix}= \begin{pmatrix} 1 & 0 & 0 \\ 0 & \cos\t(s) & \sin\t(s) \\ 0 & -\sin\t(s) & \cos\t(s)\end{pmatrix}\begin{pmatrix} \bm{d}_1 \\ \bm{d}_2 \\ \bm{d}_3\end{pmatrix}\tag{13'}\end{equation}回転行列についてはどこかで調べていただければと思います。
共通点のある一方、2つの動標構が全然違うことや具体的な位置関係については、後で例を通して解説します。
フレネフレームは曲線の曲率と捩率を計算するのに便利です(式(4)(5))。これと同様の計算をダルブーフレームでも行うと、次の量を得ます。
測地的曲率を次で定める。\begin{equation}\kappa_g(s)=\bm{d}_1'(s)\cdot \bm{d}_2(s)\tag{14}\end{equation}測地的捩率を次で定める。\begin{equation}\tau_g(s)=\bm{d}_2'(s)\cdot \bm{d}_3(s)\tag{15}\end{equation}
さらに法曲率を次で定める。\begin{equation}\kappa_n(s)=\bm{d}_1'(s)\cdot \bm{d}_3(s)\tag{16}\end{equation}
$g$ は測地的(geodesic)を表します。上2式は(4)(5)と比較すると似ています。
$\bm{d}_1'=\bm{e}_1'=\kappa\bm{e}_2$ より $\bm{d}_1'$ は曲率ベクトルであり $\bm{e}_2$ と同方向です。
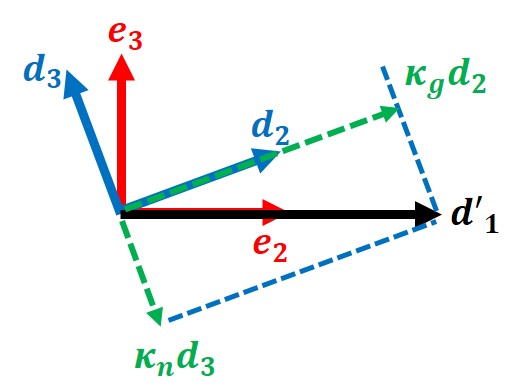
図は $\bm{e}_1$ を紙面手前に貫く向きにしたものです。定義(14)より $\kappa_g$ は $\bm{d}_1'$ を $\bm{d}_2$ と $\bm{d}_3$ 方向に分解したときの $\bm{d}_2$ 成分となります。また(16)より法曲率は残りの $\bm{d}_3$ 成分です。これの意味するところは、曲率ベクトル $\bm{d}_1'$ を曲面の接平面に正射影したもの(測地的曲率ベクトル $\kappa_g\bm{d}_2$)の大きさが測地的曲率であり、曲面の法ベクトルと曲線の接ベクトルが張る平面に正射影したもの(法曲率ベクトル $\kappa_n\bm{d}_3$)の大きさが法曲率である、となります。
法曲率についてはこちらの記事ですでに学習しましたが、まったく同じであることが分かります。したがって当然$$\kappa_n(s)=\frac{\mathrm{II}}{\mathrm{I}}$$
実際、単なる計算にしても、(14)(16)に(7)や(13)の関係を用いて\begin{eqnarray}\kappa_g(s)&=&\kappa(s)\cos\t(s)\tag{17a} \\\kappa_n(s)&=&\kappa(s)\sin\t(s)\tag{17b} \\\kappa(s)^2 &=& \kappa_g(s)^2+\kappa_n(s)^2\tag{17c}\end{eqnarray}が導けます。
さらに(15)に(7)(13)を使うと\begin{equation}\tau_g(s)=\tau(s)-\t'(s)\tag{18}\end{equation}です。
(7)(13)(13')より$$\bm{d}_1'=\kappa\bm{e}_2=\kappa\cos\t\bm{d}_2+\kappa\sin\t\bm{d}_3$$(17)によって$$\bm{d}_1'=\kappa_g\bm{d}_2+\kappa_n\bm{d}_3$$$\bm{d}_2'$ と $\bm{d}_3'$ にも同様の計算をすることにより
\begin{equation}\frac{d}{ds}\begin{pmatrix}\bm{d}_1(s)\\\bm{d}_2(s)\\\bm{d}_3(s)\end{pmatrix}=\begin{pmatrix}0 & \kappa_g(s) & \kappa_n(s)\\-\kappa_g(s) & 0 & \tau_g(s)\\-\kappa_n(s) & -\tau_g(s) & 0\end{pmatrix}\begin{pmatrix}\bm{d}_1(s)\\\bm{d}_2(s)\\\bm{d}_3(s)\end{pmatrix}\tag{19}\end{equation}
フレームの変化をフレームの線型結合で表したものです。
重要な内容ではありますが、本記事では事実のみ書いておきます。
$\kappa_g(s)=0$ を満たす曲線を測地線という。測地線は、局所的に最短距離を与える。
$\kappa$ が直線からのズレを表し、$\kappa_g$ は測地線からのズレを表します。また $\kappa_g(s)=0$ ではその定義から $\bm{d}_1'$ が $\bm{d}_2$ 方向の成分を持たず $\bm{d}_3$ に平行ということですから、測地線とは加速度ベクトル $\bm{C}''(s)$ が曲面につねに垂直となるような曲線 $\bm{C}(s)$ であるということになります。
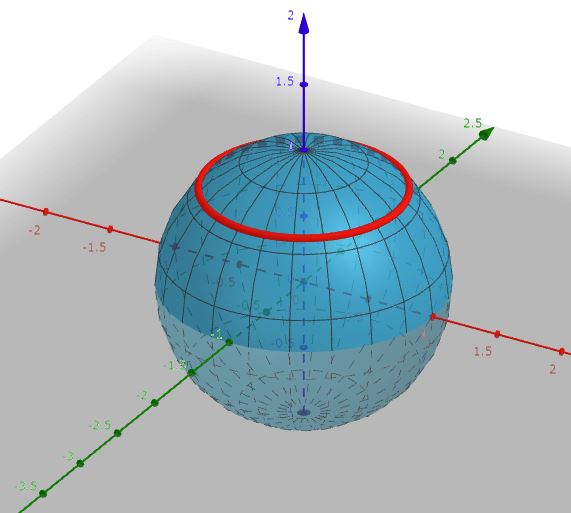
半径 $1$ の球面$$\bm{S}(u,v):=\bigl(\cos u\cos v,\cos u\sin v, \sin u\bigr)\;,\;-\frac{\pi}{2}\le u \le\frac{\pi}{2}\:,\:0\le v<2\pi$$の上にあり、かつ $z=\sin u_0$ 上にある円を考える。ただし $0\le u_0\le \frac{\pi}{2}$ とする。
(a) この円の弧長パラメータ表示を導け。
(b) フレネフレームを求めよ。
(c) 曲率 $\kappa$ と捩率 $\tau$ を求めよ。
(d) ダルブーフレームを求めよ。
(e) 測地的曲率 $\kappa_g$ と測地的捩率 $\tau_g$ および法曲率 $\kappa_n$ を求めよ。
(f) $u_0=0$ すなわち大円のときは測地線になることを確かめよ。
【解答】とりあえず $u(t)=u_0$ , $v(t)=t$ とおくと$$\bm{C}(t)=\bm{S}(u(t),v(t))=(\cos u_0\cos t,\cos u_0 \sin t,\sin u_0)$$弧長は$$s(t)=\int_0^t\sqrt{x'(t)^2+y'(t)^2+z'(t)^2}dt=t\cos u_0$$よって $t=\frac{s}{\cos u_0}$ として $u(s)=u_0$ , $v(s)=\frac{s}{\cos u_0}$.これが弧長パラメータ表示である。$$\therefore\quad\bm{C}(s)=\bm{S}(u(s),v(s))=\left(\cos u_0\cos\frac{s}{\cos u_0},\cos u_0 \sin\frac{s}{\cos u_0},\sin u_0\right)$$(1)(2)(3)よりフレネフレームは\begin{eqnarray*}\bm{e}_1(s)&=&\left(-\sin\frac{s}{\cos u_0},\cos\frac{s}{\cos u_0},0\right) \\\bm{e}_2(s)&=&\left(-\cos\frac{s}{\cos u_0},-\sin\frac{s}{\cos u_0},0\right) \\\bm{e}_3(s)&=&\left(0,0,1\right)\end{eqnarray*}となる(曲面の存在は無関係で、ただ曲線の式から求まった)。
(4)(5)より$$\kappa(s)=\frac{1}{\cos u_0}\;,\; \tau(s)=0$$この $\kappa$ は曲線が半径 $\cos u_0$ の円であること、$\tau=0$ はこれが平面曲線であることに合致する。
さて、曲面上の点における単位法ベクトルは$$\bm{n}(u,v)=\frac{\bm{S}_u\times\bm{S}_v}{|\bm{S}_u\times\bm{S}_v|}=-\bigl(\cos u\cos v,\cos u\sin v, \sin u\bigr)$$であるから $u(s)=u_0$ , $v(s)=\frac{s}{\cos u_0}$ とすれば円上の点におけるダルブーフレームの1つ$$\bm{d}_3(s)=-\left(\cos u_0\cos\frac{s}{\cos u_0},\cos u_0\sin\frac{s}{\cos u_0},\sin u_0\right)$$となる。また $\bm{d}_1=\bm{e}_1$ であり、(12)から$$\bm{d}_2(s)=\left(\sin u_0\cos\frac{s}{\cos u_0},\sin u_0\sin\frac{s}{\cos u_0},-\cos u_0\right)$$これでダルブーフレームは求まった。
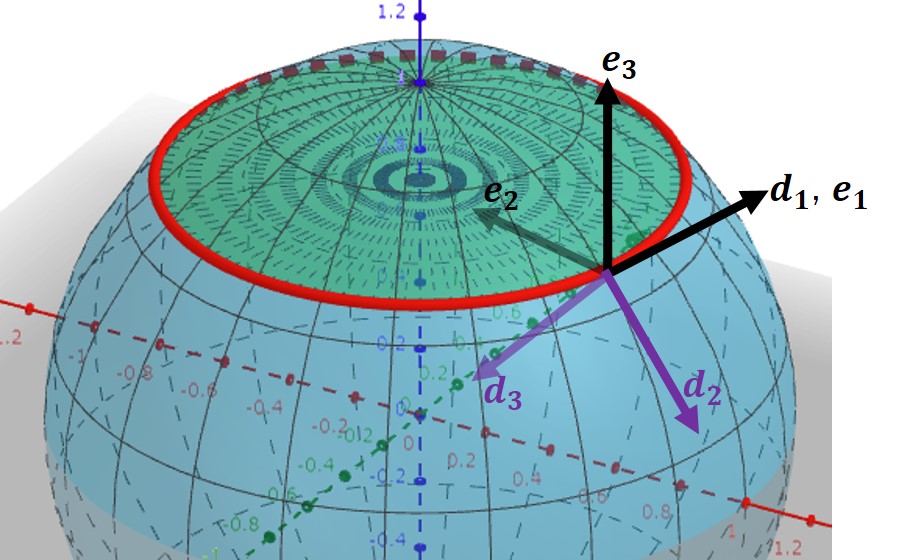
図において $\bm{d}_1=\bm{e}_1$ は円の接ベクトル、$\bm{e}_2$ は円の中心方向、$\bm{e}_3$ は $z$ 方向、$\bm{d}_2$ は球に接して $\bm{d}_1$ と直交する方向、$\bm{d}_3$ は球の中心方向となっている。また初等幾何により、$\bm{e}_1$ を軸として $\bm{e}_2$ や $\bm{e}_3$ を $\frac{\pi}{2}+u_0$ 回転させると $\bm{d}_2$ や $\bm{d}_3$ に一致する。つまり $\t(s)=\frac{\pi}{2}+u_0$ である。
地球に例えよう。図のような赤い円を地球上に描くとする。地球に立っている人からすると赤線は局所的に直線に見えるだろう。 $\bm{d}_1$ は赤線にぴったり乗ったベクトル、$\bm{d}_2$ は真南を向いたベクトル、$-\bm{d}_3$ は真上を向くベクトルである。一方 $\bm{e_3}$ は北極星の方向で、$\bm{e}_2$ は何の向きかよく分からない。そう考えると、曲面上にいる人からするとダルブーフレームのほうが分かりやすいのではないだろうか。宇宙から見る神様にはフレネフレームが良いのかも知れないけど。
さて、(14)(15)(16)から$$\kappa_g(s)=-\tan u_0\;,\;\kappa_n(s)=1\;,\;\tau_g(s)=0$$
$u_0=0$ であれば $\kappa_g=0$ より測地線である。逆に、そうでなければ測地線ではない。一般に地球の緯線は最短距離でないことはよく知られている。【解答終】
半径 $1$ の無限に長い円柱面$$\bm{S}(u,v):=(\cos u,\sin u, v)$$の上に $$u(s)=v(s)=\frac{s}{\sqrt{2}}$$なる曲線を定めると、これは常螺旋の弧長パラメータ表示である。
(a) フレネフレームを求めよ。
(b) 曲率 $\kappa$ と捩率 $\tau$ を求めよ。
(c) ダルブーフレームを求めよ。
(d) 測地的曲率 $\kappa_g$ と測地的捩率 $\tau_g$ および法曲率 $\kappa_n$ を求めよ。

【解答】フレネフレームは\begin{eqnarray*}\bm{e}_1(s)&=&\left(-\frac{1}{\sqrt{2}}\sin\frac{s}{\sqrt{2}},\frac{1}{\sqrt{2}}\cos\frac{s}{\sqrt{2}},\frac{1}{\sqrt{2}}\right) \\\bm{e}_2(s)&=&\left(-\cos\frac{s}{\sqrt{2}},-\sin\frac{s}{\sqrt{2}},0\right) \\\bm{e}_3(s)&=&\left(\frac{1}{\sqrt{2}}\sin\frac{s}{\sqrt{2}},-\frac{1}{\sqrt{2}}\cos\frac{s}{\sqrt{2}},\frac{1}{\sqrt{2}}\right)\end{eqnarray*}これより$$\kappa(s)=\frac{1}{2}\;,\;\tau(s)=\frac{1}{2}$$曲面の単位法ベクトルは $$\bm{n}=(\cos u , \sin u , 0)$$と計算されるのでダルブーフレームは\begin{eqnarray*}\bm{d}_1(s)&=&\left(-\frac{1}{\sqrt{2}}\sin\frac{s}{\sqrt{2}},\frac{1}{\sqrt{2}}\cos\frac{s}{\sqrt{2}},\frac{1}{\sqrt{2}}\right) \\\bm{d}_2(s)&=&\left(\frac{1}{\sqrt{2}}\sin\frac{s}{\sqrt{2}},-\frac{1}{\sqrt{2}}\cos\frac{s}{\sqrt{2}},\frac{1}{\sqrt{2}}\right) \\\bm{d}_3(s)&=&\left(\cos\frac{s}{\sqrt{2}},\sin\frac{s}{\sqrt{2}},0\right)\end{eqnarray*}これらより$$\kappa_g(s)=0\;,\;\kappa_n(s)=-\frac{1}{2}\;,\;\tau_g(s)=\frac{1}{2}$$
・中内伸光『幾何学は微分しないと』
・花野井 聡「曲面上の曲線と法可展面」数理解析研究所講究録1948(2015)
『幾何学は微分しないと』を参照しました。オヤジギャグまじりの平易な文章で微分幾何学を分かりやすく解説しています。初学者向けな分、内容はやや薄いと思うので、ネットや他の書籍を併用すると学習効果が高まります。

新装版 幾何学は微分しないと 〜微分幾何学入門〜【Amazon】
次:
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。


