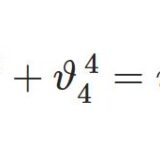前回はこちら:
前回と同様に極の個数に関する議論を使って、加法定理を導きます。テータ関数の加法定理は実に様々な形のものがあるので、あくまで一例として見ていきます。\begin{equation}F(z):=\frac{a\vartheta_3^{~2}(z)+b\vartheta_1^{~2}(z)}{\vartheta_3(z+y)\vartheta_3(z-y)}\tag{1}\end{equation}なる関数 $F(z)$ を考えます。これは $z$ の関数であり、$y$ は定数と見なします。$a,b$ は $z$ によらない定数ですが $y$ や $\tau$ にはよるかもしれません。
$F(z)$ はどんな関数でしょうか。周期性を確認しましょう。分母については\begin{align}\vartheta_3(z+1+y)&=\vartheta_3(z+y)\\\vartheta_3(z+1-y)&=\vartheta_3(z-y)\\\vartheta_3(z+\tau+y)&=q^{-1}e^{-2\pi i(z+y)}\vartheta_3(z+y)\\\vartheta_3(z+\tau-y)&=q^{-1}e^{-2\pi i(z-y)}\vartheta_3(z-y)\end{align}分子については $k=1$,$2$,$3$,$4$ について\begin{align}\vartheta_k^{~2}(z+1)&=\vartheta_k^{~2}(z)\\\vartheta_k^{~2}(z+\tau)&=q^{-2}e^{-4\pi iz}\vartheta_k^{~2}(z)\end{align}です。よって\begin{equation}F(z+1)=F(z+\tau)=F(z)\tag{2}\end{equation}よって $F(z)$ は二重周期をもち楕円関数ということになります。テータ関数は整関数ですので(1)の分母に着目して、$F(z)$ は $z=\dfrac{1+\tau}{2}\pm y$ の2か所に1位の極をもつ(可能性がある)ことが分かります。
そこでそれら極のうち1つを消してしまいましょう。つまり(1)式の分子が $\dfrac{1+\tau}{2}+y$ を零点にもてば、$F(z)$ の極としては相殺されてしまいます。そうなるためには\begin{align}a &= \frac{1}{\vartheta_3^{~2}(\frac{1+\tau}{2}+y)}\\b &=\frac{-1}{\vartheta_1^{~2}(\frac{1+\tau}{2}+y)}\end{align}とおけばよいです。半周期の変換公式から\begin{align}\vartheta_3^{~2}\left(\frac{1+\tau}{2}+y\right) &=iq^{-1/4}e^{-\pi iy}\vartheta_1(y)\\\vartheta_1^{~2}\left(\frac{1+\tau}{2}+y\right)&=q^{-1/4}e^{-\pi iy}\vartheta_3(y)\end{align}と変形しておきます。
この時点で $F(z)$ は高々1位の極を1つもつのみとなりますが、そのような楕円関数は定数関数に限ります(つまるところ極なし)。$y$ や $\tau$ には依存する可能性がある定数 $A$ を用いて\begin{equation}A\vartheta_3(z+y)\vartheta_3(z-y)=-q^{1/2}e^{2\pi iy}\left[\frac{\vartheta_3^{~2}(z)}{\vartheta_1^{~2}(y)}+\frac{\vartheta_1^{~2}(z)}{\vartheta_3^{~2}(y)}\right]\tag{3}\end{equation}$z=0$ として定数 $A$ が$$A=-q^{1/2}e^{2\pi iy}\frac{\vartheta_3^{~2}}{\vartheta_1^{~2}(y)\vartheta_3^{~2}(y)}$$のように定まります。以上から
$$\vartheta_3^{~2}\vartheta_3(z+y)\vartheta_3(z-y)=\vartheta_3^{~2}(y)\vartheta_3^{~2}(z)+\vartheta_1^{~2}(y)\vartheta_1^{~2}(z)$$
加法定理にはバリエーションがあります。(1)でどのテータ関数をチョイスするかで得られる式も少し変わってきます。
\begin{equation}G(z):=\frac{a\vartheta_2^{~2}(z)+b\vartheta_3^{~2}(z)}{\vartheta_1(z+y)\vartheta_1(z-y)}\tag{4}\end{equation}で $a,b$ を適切に定め、\begin{equation}\vartheta_4^{~2}\vartheta_1(z+y)\vartheta_1(z-y)=\vartheta_2^{~2}(y)\vartheta_3^{~2}(z)-\vartheta_3^{~2}(y)\vartheta_2^{~2}(z)\tag{5}\end{equation}なる加法定理を得よ。
周期を確認すると $G(z)$ は楕円関数だと分かる。$$$a=\frac{1}{\vartheta_2^{~2}(y)}\;,\;b =\frac{-1}{\vartheta_3^{~2}(y)}$$とすると定数 $B$ を用いて\begin{equation}B\vartheta_1(z+y)\vartheta_1(z-y)=\frac{\vartheta_2^{~2}(z)}{\vartheta_2^{~2}(y)}-\frac{\vartheta_3^{~2}(z)}{\vartheta_3^{~2}(y)}\tag{6}\end{equation}$z=0$ として $B$ が定まる。さらに$$\vartheta_2^{~2}\vartheta_3^{~2}(y)-\vartheta_3^{~2}\vartheta_2^{~2}(y)=\vartheta_4^{~2}\vartheta_1^{~2}(y)$$も用いる(前回の定理3参照)。
\begin{equation}\vartheta_4^{~2}\vartheta_2(z+y)\vartheta_2(z-y)=\vartheta_2^{~2}(y)\vartheta_4^{~2}(z)-\vartheta_3^{~2}(y)\vartheta_1^{~2}(z)\tag{7}\end{equation}なる加法定理を得よ。
(5)において $z$ に $z+1/2$ を代入することで得る。
このようにさまざまな加法定理のバリエーションがあります。ここで得た加法定理たちは $y=0$ とすることで前回得た等式と同じになることから、より一般的なものにたどりついたといえます。
\begin{equation}H(z):=\frac{a\vartheta_1(z)\vartheta_2(z)+b\vartheta_3(z)\vartheta_4(z)}{\vartheta_1(z+y)\vartheta_2(z-y)}\tag{8}\end{equation}で $a,b$ を適切に定め、\begin{equation}\vartheta_3\vartheta_4\vartheta_1(z+y)\vartheta_2(z-y)=\vartheta_1(z)\vartheta_2(z)\vartheta_3(y)\vartheta_4(y)+\vartheta_1(y)\vartheta_2(y)\vartheta_3(z)\vartheta_4(z)\tag{9}\end{equation}なる加法定理を得よ。
上でいくつかの加法定理を得ましたが、この調子でたくさんのバリエーションが得られるでしょう。すでに導出したものも含めてKharchev [2]より\begin{align} \vartheta_1(z+y)\vartheta_1(z-y)\vartheta_2^2 &= \vartheta_1^2(z)\vartheta_2^2(y)-\vartheta_2^2(z)\vartheta_1^2(y) \\ &= \vartheta_4^2(z)\vartheta_3^2(y)-\vartheta_3^2(z)\vartheta_4^2(y) \tag{10} \\ \vartheta_1(z+y)\vartheta_1(z-y)\vartheta_3^2 &= \vartheta_1^2(z)\vartheta_3^2(y)-\vartheta_3^2(z)\vartheta_1^2(y) \\ &= \vartheta_4^2(z)\vartheta_2^2(y)-\vartheta_2^2(z)\vartheta_4^2(y) \tag{11} \\ \vartheta_1(z+y)\vartheta_1(z-y)\vartheta_4^2 &= \vartheta_1^2(z)\vartheta_4^2(y)-\vartheta_4^2(z)\vartheta_1^2(y) \\ &= \vartheta_3^2(z)\vartheta_2^2(y)-\vartheta_2^2(z)\vartheta_3^2(y) \tag{12} \\ \vartheta_2(z+y)\vartheta_2(z-y)\vartheta_2^2 &= \vartheta_2^2(z)\vartheta_2^2(y)-\vartheta_1^2(z)\vartheta_1^2(y) \\ &= \vartheta_3^2(z)\vartheta_3^2(y)-\vartheta_4^2(z)\vartheta_4^2(y) \tag{13} \\ \vartheta_2(z+y)\vartheta_2(z-y)\vartheta_3^2 &= \vartheta_3^2(z)\vartheta_2^2(y)-\vartheta_1^2(z)\vartheta_4^2(y) \\ &= \vartheta_2^2(z)\vartheta_3^2(y)-\vartheta_4^2(z)\vartheta_1^2(y) \tag{14} \\ \vartheta_2(z+y)\vartheta_2(z-y)\vartheta_4^2 &= \vartheta_4^2(z)\vartheta_2^2(y)-\vartheta_1^2(z)\vartheta_3^2(y) \\ &= \vartheta_2^2(z)\vartheta_4^2(y)-\vartheta_3^2(z)\vartheta_1^2(y) \tag{15}\\ \vartheta_3(z+y)\vartheta_3(z-y)\vartheta_2^2 &= \vartheta_2^2(z)\vartheta_3^2(y)+\vartheta_1^2(z)\vartheta_4^2(y) \\ &= \vartheta_3^2(z)\vartheta_2^2(y)+\vartheta_4^2(z)\vartheta_1^2(y) \tag{16} \\ \vartheta_3(z+y)\vartheta_3(z-y)\vartheta_3^2 &= \vartheta_1^2(z)\vartheta_1^2(y)+\vartheta_3^2(z)\vartheta_3^2(y) \\ &= \vartheta_2^2(z)\vartheta_2^2(y)+\vartheta_4^2(z)\vartheta_4^2(y) \tag{17} \\ \vartheta_3(z+y)\vartheta_3(z-y)\vartheta_4^2 &= \vartheta_4^2(z)\vartheta_3^2(y)-\vartheta_1^2(z)\vartheta_2^2(y) \\ &= \vartheta_3^2(z)\vartheta_4^2(y)-\vartheta_2^2(z)\vartheta_1^2(y) \tag{18} \\ \vartheta_4(z+y)\vartheta_4(z-y)\vartheta_2^2 &= \vartheta_1^2(z)\vartheta_3^2(y)+\vartheta_2^2(z)\vartheta_4^2(y) \\ &= \vartheta_3^2(z)\vartheta_1^2(y)+\vartheta_4^2(z)\vartheta_2^2(y) \tag{19} \\ \vartheta_4(z+y)\vartheta_4(z-y)\vartheta_3^2 &= \vartheta_1^2(z)\vartheta_2^2(y)+\vartheta_3^2(z)\vartheta_4^2(y) \\ &= \vartheta_2^2(z)\vartheta_1^2(y)+\vartheta_4^2(z)\vartheta_3^2(y) \tag{20} \\ \vartheta_4(z+y)\vartheta_4(z-y)\vartheta_4^2 &= \vartheta_4^2(z)\vartheta_4^2(y)-\vartheta_1^2(z)\vartheta_1^2(y) \\ &= \vartheta_3^2(z)\vartheta_3^2(y)-\vartheta_2^2(z)\vartheta_2^2(y) \tag{21}\end{align}\begin{align} \vartheta_1(z+y)\vartheta_2(z-y)\vartheta_3\vartheta_4 &= \vartheta_1(z)\vartheta_2(z)\vartheta_3(y)\vartheta_4(y)+\vartheta_3(z)\vartheta_4(z)\vartheta_1(y)\vartheta_2(y) \tag{22} \\ \vartheta_1(z+y)\vartheta_3(z-y)\vartheta_2\vartheta_4 &= \vartheta_1(z)\vartheta_3(z)\vartheta_2(y)\vartheta_4(y)+\vartheta_2(z)\vartheta_4(z)\vartheta_1(y)\vartheta_3(y) \tag{23} \\ \vartheta_1(z+y)\vartheta_4(z-y)\vartheta_2\vartheta_3 &= \vartheta_1(z)\vartheta_4(z)\vartheta_2(y)\vartheta_3(y)+\vartheta_2(z)\vartheta_3(z)\vartheta_1(y)\vartheta_4(y) \tag{24} \\ \vartheta_2(z+y)\vartheta_3(z-y)\vartheta_2\vartheta_3 &= \vartheta_2(z)\vartheta_3(z)\vartheta_2(y)\vartheta_3(y)-\vartheta_1(z)\vartheta_4(z)\vartheta_1(y)\vartheta_4(y) \tag{25} \\ \vartheta_2(z+y)\vartheta_4(z-y)\vartheta_2\vartheta_4 &= \vartheta_2(z)\vartheta_4(z)\vartheta_2(y)\vartheta_4(y)-\vartheta_1(z)\vartheta_3(z)\vartheta_1(y)\vartheta_3(y) \tag{26} \\ \vartheta_3(z+y)\vartheta_4(z-y)\vartheta_3\vartheta_4 &= \vartheta_3(z)\vartheta_4(z)\vartheta_3(y)\vartheta_4(y)-\vartheta_1(z)\vartheta_2(z)\vartheta_1(y)\vartheta_2(y) \tag{27} \end{align}これらの式に共通するのは、左辺右辺あわせて3項の関係式になっていること、各項が4つのテータ関数($z=0$ としたものも含めて)の積になっていることです。要は$$\vartheta_i(w)\vartheta_j(x)\vartheta_k(y)\vartheta_l(z)$$をひとまとまりとして見ると(10)~(27)まですべて類似した形と言えます。このことからこれらの等式はばらばらのものではなく、上位により一般的な法則が潜んでいるような気がします。詳しくは次回にやりましょう。
(10)~(27)のうち一部の等式においては、$y=0$ とすることで前回の定理3のような関係式を得ます。よって今回の記事で導出した式たちは、前回得た式の一般化ともいえます。
第5版です。いわずと知れた名著。楕円関数にかなりのページを割いています。

こちら:
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。