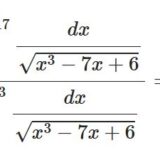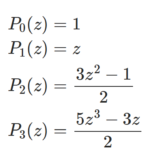楕円関数シリーズ第28回。前回は：
もくじ
前回得た公式は
\begin{align}\mathrm{sn}\frac{2Kx}{\pi} &=\frac{\pi}{kK}\sum_{n=1}^\infty\frac{\sin(2n-1)x}{\sinh\left((n-\frac{1}{2})\pi\frac{K'}{K}\right)}\tag{a}\\\mathrm{cn}\frac{2Kx}{\pi} &=\frac{\pi}{kK}\sum_{n=1}^\infty\frac{\cos(2n-1)x}{\cosh\left((n-\frac{1}{2})\pi\frac{K'}{K}\right)}\tag{b}\\\mathrm{dn}\frac{2Kx}{\pi} &=\frac{\pi}{2K}+\frac{\pi}{K}\sum_{n=1}^\infty\frac{\cos 2nx}{\cosh\left(n\pi\frac{K'}{K}\right)}\tag{c}\\[1em]\mathrm{cd}\frac{2Kx}{\pi} &=\frac{\pi}{kK}\sum_{n=1}^\infty (-1)^{n-1}\frac{\cos(2n-1)x}{\sinh\left((n-\frac{1}{2})\pi\frac{K'}{K}\right)}\tag{d}\\\mathrm{sd}\frac{2Kx}{\pi} &=\frac{\pi}{kk'K}\sum_{n=1}^\infty(-1)^{n-1}\frac{\sin(2n-1)x}{\cosh\left((n-\frac{1}{2})\pi\frac{K'}{K}\right)}\tag{e}\\\mathrm{nd}\frac{2Kx}{\pi} &=\frac{\pi}{2k'K}-\frac{\pi}{k'K}\sum_{n=1}^\infty (-1)^{n-1}\frac{\cos 2nx}{\cosh\left(n\pi\frac{K'}{K}\right)}\tag{f}\\[1em] \mathrm{ns}\frac{2Kx}{\pi} &=\frac{\pi}{2K}\csc x+\frac{2\pi}{K}\sum_{n=1}^\infty\frac{\sin(2n-1)x}{e^{(2n-1)\pi\frac{K'}{K}}-1}\tag{g}\\\mathrm{ds}\frac{2Kx}{\pi} &=\frac{\pi}{2K}\csc x-\frac{2\pi}{K}\sum_{n=1}^\infty\frac{\sin(2n-1)x}{e^{(2n-1)\pi\frac{K'}{K}}+1}\tag{h}\\\mathrm{cs}\frac{2Kx}{\pi} &=\frac{\pi}{2K}\cot x-\frac{2\pi}{K}\sum_{n=1}^\infty\frac{\sin 2nx}{e^{2n\pi\frac{K'}{K}}+1}\tag{i}\\[1em] \mathrm{dc}\frac{2Kx}{\pi} &=\frac{\pi}{2K}\sec x+\frac{2\pi}{K}\sum_{n=1}^\infty (-1)^{n-1}\frac{\cos(2n-1)x}{e^{(2n-1)\pi\frac{K'}{K}}-1}\tag{j}\\\mathrm{nc}\frac{2Kx}{\pi} &=\frac{\pi}{2k'K}\sec x-\frac{2\pi}{k'K}\sum_{n=1}^\infty (-1)^{n-1}\frac{\cos(2n-1)x}{e^{(2n-1)\pi\frac{K'}{K}}+1}\tag{k}\\\mathrm{sc}\frac{2Kx}{\pi} &=\frac{\pi}{2k'K}\tan x-\frac{2\pi}{k'K}\sum_{n=1}^\infty (-1)^{n-1}\frac{\sin 2nx}{e^{2n\pi\frac{K'}{K}}+1}\tag{l}\end{align}
これらの右辺には似ているものの少しずつ異なる級数が含まれています。
ヤコビの楕円関数は $u=0$ まわりでローラン展開（テイラー展開）できます。ベースとなる公式はこちらの命題23等をみていただくことにして、ゴリゴリ導関数を求めていくだけです。すると
\begin{align}\mathrm{sn}\:u &=u-\frac{ k^{2}+1}{6} u^{3}+\frac{ k^{4}+14 k^{2}+1}{120} u^{5}-\frac{ k^{6}+135 k^{4}+135 k^{2}+1}{5040} u^{7}+\cdots\tag{a}\\\mathrm{cn}\:u &=1-\frac{1}{2}u^2+\frac{4k^2+1}{24}u^4-\frac{16k^4+44k^2+1}{720}u^6+\cdots\tag{b}\\\mathrm{dn}\:u &=1-\frac{k^2}{2}u^2+\frac{k^4+4k^2}{24}u^4-\frac{k^6+44k^4+16k^2}{720}u^6+\cdots\tag{c}\end{align}
\begin{align}\mathrm{cd}\:u &=1+\frac{k^2-1}{2}u^2+\frac{5k^4-6k^2+1}{24}u^4+\frac{61k^6-107k^4+47k^2-1}{720}u^6+\cdots\tag{d}\\\mathrm{sd}\:u &=u+\frac{2k^2-1}{6}u^3+\frac{16k^4-16k^2+1}{120}u^5+\frac{272k^6-408k^4+138k^2-1}{5040}u^7+\cdots\tag{e}\\\mathrm{nd}\:u &=1+\frac{k^2}{2}u^2+\frac{5k^4-4k^2}{24}u^4+\frac{61k^6-76k^4+16k^2}{720}u^6+\cdots\tag{f}\end{align}
\begin{align}\mathrm{ns}\:u &=\frac{1}{u}+\frac{k^2+1}{6}u+\frac{7k^4-22k^2+7}{360}u^3+\frac{31k^6-15k^4-15k^2+31}{15120}u^5+\frac{127k^8-284k^6+186k^4-284k^2+127}{604800}u^7+\cdots\tag{g}\\\mathrm{ds}\:u &=\frac{1}{u}-\frac{2k^2-1}{6}u-\frac{8k^4-8k^2-7}{360}u^3-\frac{32k^6-48k^4+78k^2-31}{15120}u^5-\frac{128k^8-256k^6-96k^4+224k^2-127}{604800}u^7+\cdots\tag{h}\\\mathrm{cs}\:u &=\frac{1}{u}+\frac{k^2-2}{6}u+\frac{7k^4+8k^2-8}{360}u^3+\frac{31k^6-78k^4+48k^2-32}{15120}u^5+\frac{127k^8-224k^6+96k^4+256k^2-128}{604800}u^7+\cdots\tag{i}\end{align}
\begin{align}\mathrm{dc}\:u &=1-\frac{k^2-1}{2}u^2+\frac{k^4-6k^2+5}{24}u^4-\frac{k^6-47k^4+107k^2-61}{720}u^6+\cdots\tag{j}\\\mathrm{nc}\:u &=1+\frac{1}{2}u^2-\frac{4k^2-5}{24}u^4+\frac{16k^4-76k^2+61}{720}u^6+\cdots\tag{k}\\\mathrm{sc}\:u &=u-\frac{k^2-2}{6}u^3+\frac{k^4-16k^2+16}{120}u^5-\frac{k^6-138k^4+408k^2-272}{5040}u^7+\cdots\tag{l}\end{align}
定理０と定理１を合わせれば12種類の楕円関数それぞれについて等式を作れます。$\sn$ なら\begin{align}\mathrm{sn}\frac{2Kx}{\pi} &=\frac{\pi}{kK}\sum_{n=1}^\infty\frac{\sin(2n-1)x}{\sinh\left((n-\frac{1}{2})\pi\frac{K'}{K}\right)}\\&=\frac{2Kx}{\pi}-\frac{ k^{2}+1}{6} \left(\frac{2Kx}{\pi}\right)^{3}+\frac{ k^{4}+14 k^{2}+1}{120} \left(\frac{2Kx}{\pi}\right)^{5}-\cdots\end{align}といった具合です。
係数比較
１階微分において $x=0$ とすると\begin{align}\left.\frac{d}{dx}\left(\mathrm{sn}\frac{2Kx}{\pi}\right)\right|_{x=0} &=\frac{\pi}{kK}\sum_{n=1}^\infty\frac{2n-1}{\sinh\left((n-\frac{1}{2})\pi\frac{K'}{K}\right)}\\&=\frac{2K}{\pi}\end{align}となります。したがって\begin{equation}\sum_{n=1}^\infty\frac{n-\frac{1}{2}}{\sinh\left((n-\frac{1}{2})\pi\frac{K'}{K}\right)}=\frac{kK^2}{\pi^2}\tag{1}\end{equation}
同様に3階微分において $x=0$ として比較します。5階微分でもやってみます。すると以下のようになります。
\begin{align}\sum_{n=1}^\infty\frac{n-\frac{1}{2}}{\sinh\left((n-\frac{1}{2})\pi\frac{K'}{K}\right)}&=\frac{kK^2}{\pi^2}\tag{1}\\\sum_{n=1}^\infty\frac{(n-\frac{1}{2})^3}{\sinh\left((n-\frac{1}{2})\pi\frac{K'}{K}\right)}&=\frac{k(1+k^2)K^4}{\pi^4}\tag{2}\\\sum_{n=1}^\infty\frac{(n-\frac{1}{2})^5}{\sinh\left((n-\frac{1}{2})\pi\frac{K'}{K}\right)}&=\frac{k(k^4+14k^2+1)K^6}{\pi^6}\tag{3}\end{align}
このようにして次々と級数公式を得ることができます。
singular valueの代入
(1)(2)(3)でも十分な形ですが、もう少し具体的な値を出したい。(1)において $k=k_1:=1/\sqrt{2}$ とおくと $k'=k$ なので $K'/K=1$ であり、\begin{equation}K(k_1)=\frac{\G^2(\frac{1}{4})}{4\sqrt{\pi}}\tag{4}\end{equation}となります（詳細はこちらの記事を）。よって
\begin{equation}\sum_{n=1}^\infty\frac{n-\frac{1}{2}}{\sinh\left((n-\frac{1}{2})\pi\right)}=\frac{\G^4(\frac{1}{4})}{2^{9/2}\pi^3}\approx 0.246286\tag{5}\end{equation}
同様に $k=k_2:=\sqrt{2}-1$ のときは $K'/K=\sqrt{2}$ で\begin{equation}K(k_2)=\frac{\sqrt{\sqrt{2}+1}\G(\frac{1}{8})\G(\frac{3}{8})}{2^\frac{13}{4}\sqrt{\pi}}\tag{6}\end{equation}なので
\begin{equation}\sum_{n=1}^\infty\frac{n-\frac{1}{2}}{\sinh\left((n-\frac{1}{2})\pi\sqrt{2}\right)}=\frac{\G^2(\frac{1}{8})\G^2(\frac{3}{8})}{2^{13/2}\pi^3}\tag{7}\end{equation}
さらに $k=k_3:=\frac{\sqrt{6}-\sqrt{2}}{4}$ のときは $K'/K=\sqrt{3}$ で\begin{equation}K(k_3)=\frac{3^{\frac{1}{4}}\G(\frac{1}{3})^3}{2^\frac{7}{3}\pi}\tag{8}\end{equation}を用いて
\begin{equation}\sum_{n=1}^\infty\frac{n-\frac{1}{2}}{\sinh\left((n-\frac{1}{2})\pi\sqrt{3}\right)}=\frac{\sqrt{6}(\sqrt{3}-1)\G^6(\frac{1}{3})}{2^{20/3}\pi^4}\tag{8}\end{equation}
(2)や(3)についても同じようにsingular valueを代入して級数を得られます。$k_1$ のみ記しておきます。
\begin{equation}\sum_{n=1}^\infty\frac{(n-\frac{1}{2})^3}{\sinh\left((n-\frac{1}{2})\pi\right)}=\frac{3\G^8(\frac{1}{4})}{2^{19/2}\pi^6}\approx 0.128672\tag{9}\end{equation}
\begin{equation}\sum_{n=1}^\infty\frac{(n-\frac{1}{2})^5}{\sinh\left((n-\frac{1}{2})\pi\right)}=\frac{33\G^{12}(\frac{1}{4})}{2^{29/2}\pi^9}\tag{10}\end{equation}
(5)(9)(10)を眺めると規則性があるようです。
以下、残りの11種類の楕円関数に対して同様の手法で級数を求めていきます。
cnとdnについては定理０と定理１で $x=0$ とおいて比較、2階微分で $x=0$ とおいて比較、4階微分で $x=0$ とおいて比較…というふうに進めます。
\begin{align}\sum_{n=1}^\infty\frac{1}{\cosh\left((n-\frac{1}{2})\pi\frac{K'}{K}\right)}&=\frac{kK}{\pi}\tag{11}\\\sum_{n=1}^\infty\frac{(n-\frac{1}{2})^2}{\cosh\left((n-\frac{1}{2})\pi\frac{K'}{K}\right)}&=\frac{kK^3}{\pi^3}\tag{12}\\\sum_{n=1}^\infty\frac{(n-\frac{1}{2})^4}{\cosh\left((n-\frac{1}{2})\pi\frac{K'}{K}\right)}&=\frac{k(1+4k^2)K^5}{\pi^5}\tag{13}\end{align}
\begin{align}\sum_{n=1}^\infty\frac{1}{\cosh\left(n\pi\frac{K'}{K}\right)}&=\frac{K}{\pi}-\frac{1}{2}\tag{14}\\\sum_{n=1}^\infty\frac{n^2}{\cosh\left(n\pi\frac{K'}{K}\right)}&=\frac{k^2K^3}{\pi^3}\tag{15}\\\sum_{n=1}^\infty\frac{n^4}{\cosh\left(n\pi\frac{K'}{K}\right)}&=\frac{k^2(k^2+4)K^5}{\pi^5}\tag{16}\end{align}
これらに $k=k_1$ を代入すると
\begin{align}\sum_{n=1}^\infty\frac{1}{\cosh\left((n-\frac{1}{2})\pi\right)}&=\frac{\G^2(\frac{1}{4})}{2^{5/2}\pi^{3/2}}\approx 0.417313\tag{17}\\\sum_{n=1}^\infty\frac{(n-\frac{1}{2})^2}{\cosh\left((n-\frac{1}{2})\pi\right)}&=\frac{\G^6(\frac{1}{4})}{2^{13/2}\pi^{9/2}}\approx 0.145351\tag{18}\\\sum_{n=1}^\infty\frac{(n-\frac{1}{2})^4}{\cosh\left((n-\frac{1}{2})\pi\right)}&=\frac{3\G^{10}(\frac{1}{4})}{2^{21/2}\pi^{15/2}}\approx 0.151877\tag{19}\\\sum_{n=1}^\infty\frac{1}{\cosh\left(n\pi\right)}&=\frac{\G^2(\frac{1}{4})}{4\pi^{3/2}}-\frac{1}{2}\tag{20}\\\sum_{n=1}^\infty\frac{n^2}{\cosh\left(n\pi\right)}&=\frac{\G^6(\frac{1}{4})}{2^7\pi^{9/2}}\approx 0.102778\tag{21}\\\sum_{n=1}^\infty\frac{n^4}{\cosh\left(n\pi\right)}&=\frac{9\:\G^{10}(\frac{1}{4})}{2^{12}\pi^{15/2}}\approx 0.1610903\tag{22}\end{align}
こちらも同様。
\begin{align}\sum_{n=1}^\infty\frac{(-1)^{n-1}}{\sinh\left((n-\frac{1}{2})\pi\frac{K'}{K}\right)}&=\frac{kK}{\pi}\tag{23}\\\sum_{n=1}^\infty\frac{(-1)^{n-1}(n-\frac{1}{2})^2}{\sinh\left((n-\frac{1}{2})\pi\frac{K'}{K}\right)}&=\frac{k(1-k^2)K^3}{\pi^3}\tag{24}\\\sum_{n=1}^\infty\frac{(-1)^{n-1}(n-\frac{1}{2})^4}{\sinh\left((n-\frac{1}{2})\pi\frac{K'}{K}\right)}&=\frac{k(1-k^2)(1-5k^2)K^5}{\pi^5}\tag{25}\end{align}
\begin{align}\sum_{n=1}^\infty\frac{(-1)^{n-1}(n-\frac{1}{2})}{\cosh\left((n-\frac{1}{2})\pi\frac{K'}{K}\right)}&=\frac{kk'K^2}{\pi^2}\tag{26}\\\sum_{n=1}^\infty\frac{(-1)^{n-1}(n-\frac{1}{2})^3}{\cosh\left((n-\frac{1}{2})\pi\frac{K'}{K}\right)}&=\frac{kk'(1-2k^2)K^4}{\pi^4}\tag{27}\\\sum_{n=1}^\infty\frac{(-1)^{n-1}(n-\frac{1}{2})^5}{\cosh\left((n-\frac{1}{2})\pi\frac{K'}{K}\right)}&=\frac{kk'(16k^4-16k^2+1)K^6}{\pi^6}\tag{28}\end{align}
\begin{align}\sum_{n=1}^\infty\frac{(-1)^{n-1}}{\cosh\left(n\pi\frac{K'}{K}\right)}&=\frac{1}{2}-\frac{k'K}{\pi}\tag{29}\\\sum_{n=1}^\infty\frac{(-1)^{n-1}n^2}{\cosh\left(n\pi\frac{K'}{K}\right)}&=\frac{k^2k'K^3}{\pi^3}\tag{30}\\\sum_{n=1}^\infty\frac{(-1)^{n-1}n^4}{\cosh\left(n\pi\frac{K'}{K}\right)}&=\frac{k^2k'(4-5k^2)K^5}{\pi^5}\tag{31}\end{align}
これらに $k=k_1$ を代入すると
\begin{align}\sum_{n=1}^\infty\frac{(-1)^{n-1}}{\sinh\left((n-\frac{1}{2})\pi\right)}&=\frac{\G^2(\frac{1}{4})}{2^{5/2}\pi^{3/2}}\approx 0.417313\tag{32}\\\sum_{n=1}^\infty\frac{(-1)^{n-1}(n-\frac{1}{2})^2}{\sinh\left((n-\frac{1}{2})\pi\right)}&=\frac{\G^6(\frac{1}{4})}{2^{15/2}\pi^{9/2}}\approx 0.0726753\tag{33}\\\sum_{n=1}^\infty\frac{(-1)^{n-1}(n-\frac{1}{2})^4}{\sinh\left((n-\frac{1}{2})\pi\right)}&=-\frac{3\G^{10}(\frac{1}{4})}{2^{25/2}\pi^{15/2}}\approx -0.0379693\tag{34}\\\sum_{n=1}^\infty\frac{(-1)^{n-1}(n-\frac{1}{2})}{\cosh\left((n-\frac{1}{2})\pi\right)}&=\frac{\G^4(\frac{1}{4})}{2^{5}\pi^{3}}\approx 0.1741505\tag{35}\\\sum_{n=1}^\infty\frac{(-1)^{n-1}(n-\frac{1}{2})^3}{\cosh\left((n-\frac{1}{2})\pi\right)}&=0\tag{36}\\\sum_{n=1}^\infty\frac{(-1)^{n-1}(n-\frac{1}{2})^5}{\cosh\left((n-\frac{1}{2})\pi\right)}&=-\frac{3\G^{12}(\frac{1}{4})}{2^{13}\pi^{9}}\approx -0.0633805\tag{37}\\\sum_{n=1}^\infty\frac{(-1)^n}{\cosh\left(n\pi\right)}&=\frac{\G^2(\frac{1}{4})}{2^{5/2}\pi^{3/2}}-\frac{1}{2}\approx -0.0826866\tag{38}\\\sum_{n=1}^\infty\frac{(-1)^nn^2}{\cosh\left(n\pi\right)}&=-\frac{\G^6(\frac{1}{4})}{2^{15/2}\pi^{9/2}}\approx -0.0726753\tag{39}\\\sum_{n=1}^\infty\frac{(-1)^nn^4}{\cosh\left(n\pi\right)}&=-\frac{3\G^{10}(\frac{1}{4})}{2^{25/2}\pi^{15/2}}\approx -0.0379693\tag{40}\\\end{align}
また(28)に注目すると $k=k_3=\frac{\sqrt{6}-\sqrt{2}}{4}$ または $k=k_3'$ とすることで
\begin{align}\sum_{n=1}^\infty\frac{(-1)^{n-1}(n-\frac{1}{2})^5}{\cosh\left((n-\frac{1}{2})\pi\sqrt{3}\right)}&=0\tag{a}\\\sum_{n=1}^\infty\frac{(-1)^{n-1}(n-\frac{1}{2})^5}{\cosh\left((n-\frac{1}{2})\frac{\pi}{\sqrt{3}}\right)}&=0\tag{b}\end{align}
定理１から分かるようにns,ds,cs は分母にsnがあるために原点で発散します。そこで $x$ をかけて正則にします。nsの場合は$$x\:\mathrm{ns}\frac{2Kx}{\pi}=\frac{\pi}{2K}+\frac{1+k^2}{6}\frac{2K}{\pi}x+\cdots=\frac{\pi}{2K}\frac{x}{\sin x}+\frac{2\pi}{K}\sum_{n=1}^\infty\frac{x\sin(2n-1)x}{e^{(2n-1)\pi\frac{K'}{K}}-1}$$とするのです。あとは同様で $x=0$ とする、2回微分して $x=0$ とする…というように進めます。
\begin{align}\sum_{n=1}^\infty\frac{2n-1}{e^{(2n-1)\pi \frac{K'}{K}}-1}&=\frac{1+k^2}{6\pi^2}K^2-\frac{1}{24}\tag{41}\\\sum_{n=1}^\infty\frac{(2n-1)^3}{e^{(2n-1)\pi \frac{K'}{K}}-1}&=\frac{7}{240}-\frac{7k^4-22k^2+7}{15\pi^4}K^4\tag{42}\\\sum_{n=1}^\infty\frac{(2n-1)^5}{e^{(2n-1)\pi \frac{K'}{K}}-1}&=\frac{8(31k^6-15k^4-15k^2+31)}{63\pi^6}K^6-\frac{31}{504}\tag{43}\end{align}
\begin{align}\sum_{n=1}^\infty\frac{2n-1}{e^{(2n-1)\pi \frac{K'}{K}}+1}&=\frac{2k^2-1}{6\pi^2}K^2+\frac{1}{24}\tag{44}\\\sum_{n=1}^\infty\frac{(2n-1)^3}{e^{(2n-1)\pi \frac{K'}{K}}+1}&=-\frac{7}{240}-\frac{8k^4-8k^2-7}{15\pi^4}K^4\tag{45}\\\sum_{n=1}^\infty\frac{(2n-1)^5}{e^{(2n-1)\pi \frac{K'}{K}}+1}&=\frac{8(32k^6-48k^4+78k^2-31)}{63\pi^6}K^6+\frac{31}{504}\tag{46}\end{align}
\begin{align}\sum_{n=1}^\infty\frac{n}{e^{2n\pi \frac{K'}{K}}+1}&=\frac{2-k^2}{12\pi^2}K^2-\frac{1}{24}\tag{47}\\\sum_{n=1}^\infty\frac{n^3}{e^{2n\pi \frac{K'}{K}}+1}&=\frac{7k^4+8k^2-8}{120\pi^4}K^4+\frac{1}{240}\tag{48}\\\sum_{n=1}^\infty\frac{n^5}{e^{2n\pi \frac{K'}{K}}+1}&=-\frac{31k^6-78k^4+48k^2-32}{252\pi^6}K^6-\frac{1}{504}\tag{49}\end{align}
これらに $k=k_1$ を代入すると
\begin{align}\sum_{n=1}^\infty\frac{2n-1}{e^{(2n-1)\pi}-1}&=\frac{\G^4(\frac{1}{4})}{2^{6}\pi^{3}}-\frac{1}{24}\approx 0.04540858\tag{50}\\\sum_{n=1}^\infty\frac{(2n-1)^3}{e^{(2n-1)\pi}-1}&=\frac{3}{5}\frac{\G^8(\frac{1}{4})}{2^{10}\pi^{6}}+\frac{7}{240}\approx 0.0473637\tag{51}\\\sum_{n=1}^\infty\frac{(2n-1)^5}{e^{(2n-1)\pi}-1}&=\frac{3\G^{12}(\frac{1}{4})}{2^{12}\pi^{9}}-\frac{31}{504}\approx 0.06525297\tag{52}\\\sum_{n=1}^\infty\frac{2n-1}{e^{(2n-1)\pi}+1}&=\frac{1}{24}\tag{53}\\\sum_{n=1}^\infty\frac{(2n-1)^3}{e^{(2n-1)\pi}+1}&=\frac{3}{5}\frac{\G^8(\frac{1}{4})}{2^{8}\pi^{6}}-\frac{7}{240}\approx 0.0436215\tag{54}\\\sum_{n=1}^\infty\frac{(2n-1)^5}{e^{(2n-1)\pi}+1}&=\frac{31}{504}\tag{55}\\\sum_{n=1}^\infty\frac{n}{e^{2n\pi}+1}&=\frac{\G^4(\frac{1}{4})}{2^{7}\pi^{3}}-\frac{1}{24}\approx 0.00187096\tag{56}\\\sum_{n=1}^\infty\frac{n^3}{e^{2n\pi}+1}&=\frac{1}{240}-\frac{3}{5}\frac{\G^8(\frac{1}{4})}{2^{13}\pi^{6}}\approx 0.00189204\tag{57}\\\sum_{n=1}^\infty\frac{n^5}{e^{2n\pi}+1}&=-\frac{1}{504}+\frac{3\G^{12}(\frac{1}{4})}{2^{17}\pi^{9}}\approx 0.00197715\tag{58}\end{align}
(53)(55)のシンプルさは驚きです。
これまでのやりかたと同じです。
\begin{align}\sum_{n=1}^\infty\frac{(-1)^{n-1}}{e^{(2n-1)\pi \frac{K'}{K}}-1}&=\frac{K}{2\pi}-\frac{1}{4}\tag{59}\\\sum_{n=1}^\infty\frac{(-1)^{n-1}(2n-1)^2}{e^{(2n-1)\pi \frac{K'}{K}}-1}&=\frac{1}{4}-\frac{2(1-k^2)}{\pi^3}K^3\tag{60}\\\sum_{n=1}^\infty\frac{(-1)^{n-1}(2n-1)^4}{e^{(2n-1)\pi \frac{K'}{K}}-1}&=\frac{8(k^2-1)(k^2-5)}{\pi^5}K^5-\frac{5}{4}\tag{61}\end{align}
\begin{align}\sum_{n=1}^\infty\frac{(-1)^{n-1}}{e^{(2n-1)\pi \frac{K'}{K}}+1}&=-\frac{k'K}{2\pi}+\frac{1}{4}\tag{62}\\\sum_{n=1}^\infty\frac{(-1)^{n-1}(2n-1)^2}{e^{(2n-1)\pi \frac{K'}{K}}+1}&=\frac{2k'}{\pi^3}K^3-\frac{1}{4}\tag{63}\\\sum_{n=1}^\infty\frac{(-1)^{n-1}(2n-1)^4}{e^{(2n-1)\pi \frac{K'}{K}}+1}&=-\frac{8k'(5-4k^2)}{\pi^5}K^5+\frac{5}{4}\tag{64}\end{align}
\begin{align}\sum_{n=1}^\infty\frac{(-1)^{n-1}n}{e^{2n\pi \frac{K'}{K}}+1}&=-\frac{k'}{2\pi^2}K^2+\frac{1}{8}\tag{65}\\\sum_{n=1}^\infty\frac{(-1)^{n-1}n^3}{e^{2n\pi \frac{K'}{K}}+1}&=\frac{k'(2-k^2)}{2\pi^4}K^4-\frac{1}{16}\tag{66}\\\sum_{n=1}^\infty\frac{(-1)^{n-1}n^5}{e^{2n\pi \frac{K'}{K}}+1}&=-\frac{k'(k^4-16k^2+16)}{2\pi^6}K^6+\frac{1}{8}\tag{67}\end{align}
これらに $k=k_1$ を代入すると
\begin{align}\sum_{n=1}^\infty\frac{(-1)^{n-1}}{e^{(2n-1)\pi}-1}&=\frac{\G^2(\frac{1}{4})}{2^{3}\pi^{3/2}}-\frac{1}{4}\approx 0.0450851\tag{68}\\\sum_{n=1}^\infty\frac{(-1)^{n-1}(2n-1)^2}{e^{(2n-1)\pi}-1}&=-\frac{\G^6(\frac{1}{4})}{2^{6}\pi^{9/2}}+\frac{1}{4}\approx 0.0444431\tag{69}\\\sum_{n=1}^\infty\frac{(-1)^{n-1}(2n-1)^4}{e^{(2n-1)\pi}-1}&=\frac{9\G^{10}(\frac{1}{4})}{2^{9}\pi^{15/2}}-\frac{5}{4}\approx 0.0387220\tag{70}\\\sum_{n=1}^\infty\frac{(-1)^{n-1}}{e^{(2n-1)\pi}+1}&=-\frac{\G^2(\frac{1}{4})}{2^{7/2}\pi^{3/2}}+\frac{1}{4}\approx 0.0413433\tag{71}\\\sum_{n=1}^\infty\frac{(-1)^{n-1}(2n-1)^2}{e^{(2n-1)\pi}+1}&=\frac{\G^6(\frac{1}{4})}{2^{11/2}\pi^{9/2}}-\frac{1}{4}\approx 0.0407013\tag{72}\\\sum_{n=1}^\infty\frac{(-1)^{n-1}(2n-1)^4}{e^{(2n-1)\pi}+1}&=-\frac{3\G^{10}(\frac{1}{4})}{2^{15/2}\pi^{15/2}}+\frac{5}{4}\approx 0.0349812\tag{73}\\\sum_{n=1}^\infty\frac{(-1)^{n-1}n}{e^{2n\pi}+1}&=-\frac{\G^4(\frac{1}{4})}{2^{11/2}\pi^{3}}+\frac{1}{8}\approx 0.00185701\tag{74}\\\sum_{n=1}^\infty\frac{(-1)^{n-1}n^3}{e^{2n\pi}+1}&=\frac{3\G^8(\frac{1}{4})}{2^{21/2}\pi^{6}}-\frac{1}{16}\approx 0.00183624\tag{75}\\\sum_{n=1}^\infty\frac{(-1)^{n-1}n^5}{e^{2n\pi}+1}&=-\frac{33\G^{12}(\frac{1}{4})}{2^{31/2}\pi^{9}}+\frac{1}{8}\approx 0.00175394\tag{76}\end{align}
ほかにもいろいろ考えられます。例えば $\mathrm{ns}^2$ みたいなのを展開するとか。
Please support me!
記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。
