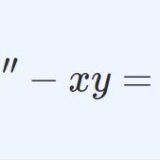「ガンマ関数の基礎」シリーズ第11回は積分表示です。本シリーズではそもそもガンマ関数を積分表示で定義しています。\begin{equation}\G(z)=\int_0^\infty e^{-t}t^{z-1}dt\quad(\mathfrak{R}z>0)\tag{1}\end{equation}これを第1番目の積分表示として、今回は以下の表式を取り上げます。
$n$ 階導関数の積分表示\begin{equation}\G^{(n)}(z)=\int_0^\infty e^{-t}t^{z-1}(\log t)^ndt\quad(\mathfrak{R}z>0)\tag{2}\end{equation}指数の変換\begin{equation}\G(z)=s^z\int_0^\infty e^{-st}t^{z-1}dt\quad(s>0,\mathfrak{R}z>0)\tag{3}\end{equation}オイラーによる表示\begin{equation}\G(z)=\int_0^1\left(\log\frac{1}{x}\right)^{z-1}dx\quad(\mathfrak{R}z>0)\tag{4}\end{equation}
ハンケルの積分表示3つ\begin{equation}\G(z)=\frac{e^{-i\pi z}}{2i\sin\pi z}\int_C e^{-t}t^{z-1}dt\quad(z\notin\ZZ)\tag{5}\end{equation}\begin{equation}\G(z)=-\frac{1}{2i\sin\pi z}\int_C e^{-t}(-t)^{z-1}dt\quad(z\notin\ZZ)\tag{6}\end{equation}\begin{equation}\frac{1}{\G(z)}=\frac{i}{2\pi}\int_C e^{-t}(-t)^{-z}dt\tag{7}\end{equation}※ 経路 $C$ はハンケル積分路
上3つは簡単です(極限操作等の細かいことを気にしなければ)。その下は複素積分であらわされていますので、少々手が込んでいます。
前回の記事はこちら。本記事とあまり関連ありません。
【γ10】ポリガンマ関数の値、極、級数表示、ゼータ関数との関係(ガンマ関数の基礎シリーズ10)
(1)を1回微分すると、指数関数の微分を意識して$$\G'(z)=\int_0^\infty e^{-t}t^{z-1}(\log t)dt$$となります。繰り返すと(2)を得ます。
(1)において正の実数 $s$ に対して $t=sx$ と置換すると$$\G(z)=\int_0^\infty e^{-sx}(sx)^{z-1}sdx$$となって(3)を得ます。
Whittaker&Watsonによると(4)式は1730年にオイラーが示したものらしいです。右辺の積分で $\log\dfrac{1}{x}=t$ とおけば$$\int_\infty^0t^{z-1}(-e^{-t})dt$$となってガンマ関数に等しいことが示されました。
古いですが有名な書物で、どんどん改訂版が出ています。前半は解析学一般、後半は特殊関数という内容で、網羅的に勉強できます。演習問題に解答がないのが昔ながらのものって感じ。2022/11/6現在、最新版は5th Editionで私も所有していますが、廉価な3rdとかでも十分かと。

A Course of Modern Analysis: fifth Edition

A Course of Modern Analysis: Third Edition
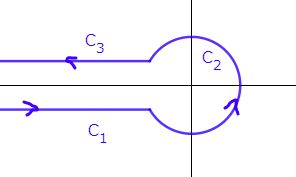
今日のメインです。複素平面におけるハンケル積分路 $C$ は、実軸上の点 $R$ から実軸に沿って原点をまわり、 また実軸に沿って $R$ に戻るものです。そして $R\to\infty$ とします。

この積分路を次のように変更しても(5)や(6)の積分値は変わりません。$C_1$ , $C_3$ は実軸ぎりぎりに沿わせ $C_3$ は半径 $\epsilon$ の小さな円を描きます。

これから考える被積分関数 $e^{-t}t^{z-1}$ は、$t$ の偏角が $0\to2\pi$ へ変化すると値が元に戻りません。よって原点回りにピッタリ1回転させるのは避けねばならないのです。
その1
$$\int_C e^{-t}t^{z-1}dt$$なる積分を考えます。$$\int_C=\int_{C_1}+\int_{C_2}+\int_{C_3}$$より3つの経路に分けて考えます。$t$ の偏角は $0$ から $2\pi$ までとるとします。つまり $t=re^{i\t}$ とおいたとき $0<\t<2\pi$ です。
まず $C_1$ について。$\t=+0$ なので$t=r$ です。$r$ は $\infty\to0$ と変化します。よって$$\int_{C_1}e^{-t}t^{z-1}dt=\int_{\infty}^0e^{-r}r^{z-1}dr$$ガンマ関数の定義を思い起こせば$$\therefore\quad\int_{C_1}e^{-t}t^{z-1}dt=-\G(z)$$
次に $C_2$ です。$t=\epsilon e^{i\t}$ とおいて $\t$ を $0\to 2\pi$ と変化させます。よって\begin{eqnarray*}\int_{C_2}e^{-t}t^{z-1}dt&=&\int_{0}^{2\pi}e^{-\epsilon(\cos\t+i\sin\t)}(\epsilon e^{i\t})^{z-1}i\epsilon e^{i\t}d\t\\&=&i\epsilon^z\int_{0}^{2\pi}e^{-\epsilon(\cos\t+i\sin\t)}e^{i\t z}d\t\\&&\xrightarrow[\epsilon\to0]{}0\end{eqnarray*}
最後に $C_3$ です。$\t=2\pi$ なので$t=re^{2\pi i}$ です。$r$ は $0\to\infty$ と変化します。よって\begin{eqnarray*}\int_{C_3}e^{-t}t^{z-1}dt&=&\int_0^{\infty}e^{-r}(re^{2\pi i})^{z-1}e^{2\pi i}dr\\&=&\int_0^{\infty}e^{-r}r^{z-1}e^{2\pi iz}dr\\&=&e^{2\pi iz}\G(z)\end{eqnarray*}
さて、3つの経路をつなぎましょう。$$\int_C e^{-t}t^{z-1}dt=-\G(z)+0+e^{2\pi iz}\G(z)$$$$\therefore\quad\G(z)=\frac{1}{e^{2\pi iz}-1}\int_C e^{-t}t^{z-1}dt$$これでおわりでもいいのですが、次のように変形することもあります。$$\frac{1}{e^{2\pi iz}-1}=\frac{e^{-\pi iz}}{e^{\pi iz}-e^{-\pi iz}}=\frac{e^{-\pi iz}}{2i\sin\pi z}$$以上からハンケルの積分表示その1が示されました!
$$\G(z)=\frac{e^{-i\pi z}}{2i\sin\pi z}\int_C e^{-t}t^{z-1}dt\quad(z\notin\ZZ)$$
その2
$$\int_C e^{-t}(-t)^{z-1}dt$$なる積分を考えます。$$\int_C=\int_{C_1}+\int_{C_2}+\int_{C_3}$$より3つの経路に分けて考えます。今回は $-t=re^{i\t}$ なる置換をします。$-t$ の平面を考えると図2と原点対称の経路になりますので$-t$ の偏角 $\t$は $-\pi$ から $\pi$ までとることになります。
まず $C_1$ です。$\t=-\pi$ なので$-t=re^{-i\pi}$ です。$r$ は $\infty\to0$ と変化します。よって\begin{eqnarray*}\int_{C_1}e^{-t}(-t)^{z-1}dt&=&\int_{\infty}^0e^{-r}(re^{-i\pi})^{z-1}(-e^{-i\pi}dr)\\&=&\int_0^\infty e^{-r}r^{z-1}e^{-i\pi z}dr\\&=&e^{-i\pi z}\G(z)\end{eqnarray*}
次に $C_2$ は $-t=\epsilon e^{i\t}$ として $\t$ を $-\pi$ から $\pi$ まで積分します。 「その1」と同様 $0$ に収束します。
最後は $C_3$ です。$\t=\pi$ なので$-t=re^{i\pi}$ です。$r$ は $0$ から $\infty$ へ変化します。よって\begin{eqnarray*}\int_{C_3}e^{-t}(-t)^{z-1}dt&=&\int_0^{\infty}e^{-r}(re^{i\pi})^{z-1}(-e^{i\pi}dr)\\&=&-\int_0^\infty e^{-r}r^{z-1}e^{i\pi z}dr\\&=&-e^{i\pi z}\G(z)\end{eqnarray*}
以上から$$\int_C e^{-t}(-t)^{z-1}dt=e^{-i\pi z}\G(z)+0-e^{i\pi z}\G(z)$$式を変形すると以下のような2つめのハンケル表示ができます!
\begin{equation}\G(z)=-\frac{1}{2i\sin\pi z}\int_C e^{-t}(-t)^{z-1}dt\quad(z\notin\ZZ)\tag{8}\end{equation}
その3(相反公式による)
(8)で $z$ に $1-z$ を代入すると$$\G(1-z)=-\frac{1}{2i\sin\pi z}\int_C e^{-t}(-t)^{-z}dt$$ガンマ関数の相反公式$$\G(z)\G(1-z)=\frac{\pi}{\sin\pi z}$$によって
$$\frac{1}{\G(z)}=\frac{i}{2\pi}\int_C e^{-t}(-t)^{-z}dt$$
これが最後のハンケル表示です。ちなみに相反公式の導出については次の記事をご参照:
【γ2】ガンマ関数の3つの乗積表示と相反公式(ガウス・オイラー・ワイエルシュトラス)
ハンケルの表示$$\frac{1}{\G(z)}=\frac{i}{2\pi}\int_C e^{-t}(-t)^{-z}dt$$を用いて $\G(1/2)$ が求まるか確認せよ。
$-t=xe^{i\t}$ の形に置換し、図3の経路をとります。$C_2$ の経路は $\epsilon\to0$ でゼロになることがすぐに分かります。\begin{eqnarray*}\int_C e^{-t}(-t)^{-\frac{1}{2}}dt&=&-\int_\infty^0e^{-x}(xe^{-i\pi})^{-\frac{1}{2}}e^{-i\pi}dx-\int_\infty^0e^{-x}(xe^{i\pi})^{-\frac{1}{2}}e^{i\pi}dx\\ &=& -i\int_0^\infty e^{-x}x^{-\frac{1}{2}}dx-i\int_\infty^0e^{-x}x^{-\frac{1}{2}}dx \\ &=& -2i\int_0^\infty e^{-x}x^{-\frac{1}{2}}dx \\ &=& -2\sqrt{\pi}i\end{eqnarray*}したがって$$\frac{1}{\G(1/2)}=\frac{i}{2\pi}(-2\sqrt{\pi}i)=\frac{1}{\sqrt{\pi}}$$$$\therefore\quad\G(1/2)=\sqrt{\pi}$$
ハンケルの表示$$\frac{1}{\G(z)}=\frac{i}{2\pi}\int_C e^{-t}(-t)^{-z}dt$$において、経路 $C$ を次のように定める。$+\infty+i$ より出発し、実軸に平行に進み $i$ に至る($C_1$)。原点回りを半周して $-i$ に至る($C_2$)。実軸に沿って $+\infty-i$ へ進む($C_3$)。$z=-\frac{3}{2}$ のとき、この積分を数値計算して $\G(-3/2)=\frac{4\sqrt{\pi}}{3}$ であることを確かめよ。
$C_1$ で $-t=x-i$ , $C_2$ で $-t=e^{i\t}$ , $C_3$ で $-t=x+i$ と置換すると\begin{eqnarray*}\int_C e^{-t}(-t)^{\frac{3}{2}}dt &=& -\int_{-\infty}^0 e^{x-i}(x-i)^{\frac{3}{2}}dx-i\int_{-\frac{\pi}{2}}^\frac{\pi}{2}e^{e^{i\t}}(e^{\frac{3}{2}i\t})e^{i\t}dt-\int_0^{-\infty}e^{x+i}(x+i)^{\frac{3}{2}}dx\\ &=& -e^{-i}\int_{-\infty}^0 e^{x}(x-i)^{\frac{3}{2}}dx-i\int_{-\frac{\pi}{2}}^\frac{\pi}{2}e^{e^{i\t}}e^{\frac{5}{2}i\t}dt-e^i\int_0^{-\infty}e^{x}(x+i)^{\frac{3}{2}}dx\\ &=& -i\int_{-\frac{\pi}{2}}^\frac{\pi}{2}e^{e^{i\t}}e^{\frac{5}{2}i\t}dt+2i\mathrm{Im}e^i\int_{-\infty}^0e^{x}(x+i)^{\frac{3}{2}}dx \\ &\approx&0.780136i-3.43882i\\ &=& -2.65868i\end{eqnarray*}したがって$$\frac{i}{2\pi}\int_C e^{-t}(-t)^{\frac{3}{2}}dt \approx 0.423142 \approx \frac{3}{4\sqrt{\pi}}$$
以上で冒頭の6つの積分表示を導出できました!なおハンケル積分路による積分はゼータ関数など多くの特殊関数の解析接続に使われるなど、応用性があるので、手を動かして練習するのがおすすめです!
次の記事はシリーズとは独立しています。高校数学で理解できる2本立て:
ガンマ関数の基礎シリーズの次回はこちら!:
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。