微分幾何学の講座・第4回。前回に引き続き、空間曲線に関する様々な事項を取り上げます。今回は接線、主法線、従法線、法平面、接触平面の式について考えます。
前回はこちら:
空間曲線1-弧長パラメータと動標構、曲率・捩率、フレネ・セレの公式
もくじ
今回も弧長パラメータ表示で進めていきます。曲線 $$c(s):=\left(x(s),y(s),z(s)\right)$$はベクトルですが、太字にしたり矢印はつけないことにします。動標構は次のように定義されるのでした。
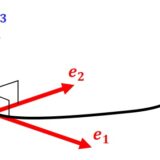
曲線 $c(s)$ における動標構は以下で定める単位接ベクトル $e_1(s)$、単位主法線ベクトル $e_2(s)$、単位従法線ベクトル $e_3(s)$ の組である。\begin{eqnarray}e_1(s)&:=&c'(s)\tag{5} \\ e_2(s) &:=& \frac{c''(s)}{|c''(s)|}\tag{6} \\ e_3(s)&:=&e_1(s)\times e_2(s)\tag{0}\end{eqnarray}
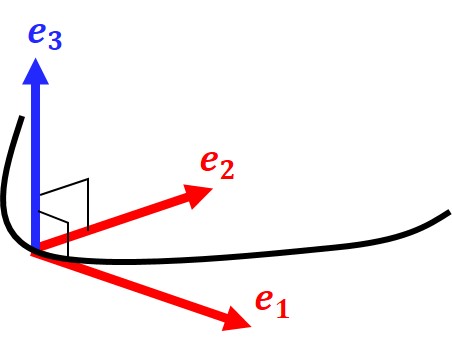
接点 $c(s_0)$ とすると、曲線の接線は位置 $c(s_0)$ を通って $e_1(s_0)$ の方向にある点の集合です。したがって接線上の任意の点を $\bm{p}$ とすれば
\begin{equation}\bm{p}=c(s_0)+\lambda e_1(s_0)\quad,\quad\lambda\in\RR\tag{1}\end{equation}
以下、パラメータ $\lambda\in\RR$ としておきます。主法線は $e_2(t_0)$ の方向を考えるとよいですから
\begin{equation}\bm{p}=c(s_0)+\lambda e_2(s_0)\tag{2}\end{equation}
図1から分かるように
\begin{equation}\bm{p}=c(s_0)+\lambda e_3(s_0)\tag{3}\end{equation}
$e_1$ と $e_2$ が張る平面を接触平面(osculating plane)とよび、曲線が局所的に乗っている平面です。
図1または2より明らかに、従法線は接触平面の法線方向に伸びています。よって接触平面上の任意の点 $\bm{p}$ は次の方程式を満たします。
\begin{equation}\left(\bm{p}-c(s_0)\right)\cdot e_3(s_0)=0\tag{4}\end{equation}
$e_2$ と $e_3$ が張る平面を法平面(normal plane)とよび、接線と垂直に交わっています。よって
\begin{equation}\left(\bm{p}-c(s_0)\right)\cdot e_1(s_0)=0\tag{5}\end{equation}
$e_3$ と $e_1$ が張る平面を展直平面(rectifying plane)とよび、主法線と垂直に交わっています。よって
\begin{equation}\left(\bm{p}-c(s_0)\right)\cdot e_2(s_0)=0\tag{6}\end{equation}
2つの関数 $f,g$ があり、ともに空間曲線を表すとします。このとき、$s_0$ において2つが同じ値をとるとき(すなわち交わるとき)、この状況を「0次接触」といいます。その上で2つが同じ微分係数をもつとき(すなわち接するとき)、「1次接触」といいます。さらに2つが同じ2階微分係数をもつとき「2次接触」といい、加えて3階微分係数が一致するとき「3次接触」といいます。
もう少し詳しく言えば、前回説明したブーケの公式
\begin{eqnarray}c(s) &=& c(s_0)+(s-s_0)e_1(s_0)+\frac{(s-s_0)^2}{2}\kappa(s_0)e_2(s_0)\\&&+\frac{(s-s_0)^3}{6}\left\{-\kappa^2(s_0) e_1(s_0)+\kappa'(s_0) e_2(s_0)+\kappa(s_0)\tau(s_0) e_3(s_0)\right\}\\&&+O\bigl((s-s_0)^4\bigr)\tag{7}\end{eqnarray}
を用いて、$\D s:=s-s_0$ の $n$ 次まで一致していれば $n$ 次の接触をなすというわけです。
以下では曲線 $c(s)$ へ接触する直線、円、球について考えましょう。
曲線 $c(s)$ の $s=s_0$ における接線の弧長パラメータ表示は\begin{equation}c(s)=c(s_0)+e_1(s_0)(s-s_0)\tag{8}\end{equation}です($|c'(s)|=1$ となっている)。(7)と比較すると曲線は明らかに接線と1次の接触をなします。
また $c(s)$ と接線の離れ具合を幾何学的に捉える事実として、$c(s)$ における接線に $c(s+\D s)$ から下ろした垂線の足の長さを $\D h$ とするとき\begin{equation}\lim_{\D s\to0}\frac{\D h}{(\D s)^2}=\frac{\kappa(s)}{2}\tag{9}\end{equation}を示すことができます(前回記事)。$\D h$ は「離れ具合」を長さで表したものであり、オーダーとしては $\D h\approx \D s^2$ ということになります。
$c(s)$ は $s=s_0$ においてある円と二次接触をします。この円を「接触円」とよびます。
(7)によれば $\D s:=s-s_0$ とおくと曲線の式は\begin{equation}c(s) = c(s_0)+e_1(s_0)\D s+\frac{\kappa(s_0)}{2}e_2(s_0)\D s^2+O\bigl(\D s^3\bigr)\tag{10}\end{equation}とできます。ここで位置 $\bm{a}(s_0)$ を定義します。\begin{equation}\bm{a}(s_0):=c(s_0)+\frac{1}{\kappa(s_0)}e_2(s_0)\tag{11}\end{equation}$\bm{a}(s_0)$ は $c(s_0)$ から主法線の方向に $1/\kappa(s_0)$ の距離を進んだ点です。整理すると$$c(s)-\bm{a}(s_0)=e_1(s_0)\D s+\left(\frac{\kappa(s_0)}{2}\D s^2-\frac{1}{\kappa(s_0)}\right)e_2(s_0)+O\bigl(\D s^3\bigr)$$自身との内積をとると$$|c(s)-\bm{a}(s_0)|^2=\D s^2+\left[\frac{\kappa(s_0)}{2}\D s^2-\frac{1}{\kappa(s_0)}\right]^2+O\bigl(\D s^3\bigr)$$$$\therefore\quad |c(s)-\bm{a}(s_0)|^2=\frac{1}{\kappa(s_0)^2}+O\bigl(\D s^3\bigr)$$平方根をとって微小量に関する近似をとると\begin{equation} |c(s)-\bm{a}(s_0)|=\frac{1}{\kappa(s_0)}+O\bigl(\D s^3\bigr)\tag{12}\end{equation}微小量を無視すれば\begin{equation} |c(s)-\bm{a}(s_0)|=\frac{1}{\kappa(s_0)}\tag{13}\end{equation}これは $\bm{a}(s_0)$ を中心とする半径 $\dfrac{1}{\kappa(s_0)}$ の円を表します。なお$$\rho(s):=\dfrac{1}{\kappa(s_0)}$$を曲率半径といいます。
(10)と(12)は $\D s$ の少なくとも2次まで一致しています。よって $c(s)$ と(13)の円は二次接触をなしており、この円が $s=s_0$ における接触円です。
なお、逆にまず円の方程式を導出し、変形して(10)を導くこともできます。概略だけ説明しますと、曲線 $c(s)$ に接触する円上の点 $\bm{p}$ は $s=s_0$ の接触平面上にあるため $\bm{p}=p_1 e_1(s_0)+p_2 e_2(s_0)$ とおけます。 この円の半径を $\dfrac{1}{\kappa(s_0)}$、中心を $c(s_0)+\frac{1}{\kappa(s_0)}e_2(s_0)$ とすると$$p_1^2=p_2\left(\frac{2}{\kappa(s_0)}-p_2\right)$$なる関係から$$\bm{p}=c(s_0)+\sqrt{p_2\left(\frac{2}{\kappa(s_0)}-p_2\right)}e_1(s_0)+p_2e_2(s_0)\;,0\le p_2\le 2\rho(s_0)$$$p_2$ を微小量 $\dfrac{\kappa(s_0)}{2}\D s^2$ ととると(10)を得ます。
話題を変えます。先ほどのように「離れ具合」も見てみましょう。

円と曲線は接点 $c(s)$ 付近で互いに近似できますが、そこから $\D s$ 進んだ曲線状の点 $c(s+\D s)$ が円から乖離している距離 $\D h$ を求めてみましょう。$e_2$ と $\tilde{e}_2$ がなす角 $\D\t$ は扇形の中心角と等しく\begin{equation}\kappa(s)=\frac{d\t}{ds}\tag{14}\end{equation}であることおよび$$\D\t=\t'(s)\D s+\frac{\t''(s)}{2}\D s^2+O(\D s^3)$$と展開できますので\begin{equation}\D\t=\kappa\D s+\frac{\kappa'(s)}{2}\D s^2+O(\D s^3)\tag{15}\end{equation}また回転を考えることにより$$\tilde{e_2}(s)=\cos\D\t e_2(s)-\sin\D\t e_1(s)$$なので\begin{equation}\tilde{e_2}(s)=\left(1-\frac{\D\t^2}{2}\right)e_2(s)-\left(\D\t-\frac{\D\t^3}{6}\right)e_1(s)+O(\D s^4)\tag{15}\end{equation}最後に曲率円の中心 $\bm{a}(s)$ と半径 $\rho(s)$ により\begin{equation}\bigl(c(s+\D s)-\bm{a}(s)\bigr)\cdot \tilde{e_2}(s)=-\rho(s)-\D h\tag{16}\end{equation}これらと(11)を合わせることにより$$\frac{\D h}{\D s^3}=-\frac{\kappa'(s)}{6}+O(\D s)$$よってオーダーとしては $\D h\approx\D s^3$ であり、(9)と比較してより接近していることが分かります。
曲線は $s$ においてある球と三次接触をします。$s$ から $\D s$ 動いた点における三次までの曲線の式は、少し整理して\begin{eqnarray}c(s+\D s) &=& c(s)+\left(\D s-\frac{\kappa(s)^2}{6}\D s^3\right)e_1(s)\\&&+\left(\frac{\kappa(s)}{2}\D s^2+\frac{\kappa'(s)}{6}\D s^3\right)e_2(s)+\frac{\kappa(s)\tau(s)}{6}\D s^3 e_3(s)\\&&+O\bigl(\D s^4\bigr)\tag{17}\end{eqnarray}ここで位置 $\bm{b}(s)$ を定義します。\begin{equation}\bm{b}(s):=c(s)+\frac{1}{\kappa(s)}e_2(s)-\frac{\kappa'(s)}{\tau(s)\kappa(s)^2}e_3(s)\tag{18}\end{equation}(11)と比べると、$\bm{b}$ は曲率中心 $\bm{a}$ から従法線ベクトルの方向に少しずれた位置になっています。すると\begin{eqnarray*}c(s+\D s)-\bm{b}(s) &=& \left(\D s-\frac{\kappa(s)^2}{6}\D s^3\right)e_1(s)\\&&+\left(\frac{\kappa(s)}{2}\D s^2+\frac{\kappa'(s)}{6}\D s^3-\frac{1}{\kappa(s)}\right)e_2(s)\\&&+\left(\frac{\kappa(s)\tau(s)}{6}\D s^3-\frac{\kappa'(s)}{\tau(s)\kappa(s)^2}\right) e_3(s)\\&&+O\bigl(\D s^4\bigr)\end{eqnarray*}両辺の内積をとって\begin{equation}|c(s+\D s)-\bm{b}(s)|=\sqrt{\frac{1}{\kappa(s)^2}+\left(\frac{\kappa'(s)}{\tau(s)\kappa(s)^2}\right)^2}+O\bigl(\D s^4\bigr)\tag{19}\end{equation}これは中心 $\bm{b}(s)$ で半径が右辺である球を表す式です。(19)は(17)からの単純な式変形で得られたものなので、(17)と(19)は $\D s$ の3次までは一致しています。よって $s$ 付近では曲線 $c(s)$ と球(19)は3次の接触をなします。この球を接触球といいます。
これはすなわち、接触球(19)上のある曲線が $c(s)$ に局所的に一致しているということです。
曲率半径 $\rho=1/\kappa$ を使えば(18)は\begin{equation}\bm{b}(s):=c(s)+\rho(s)e_2(s)+\frac{\rho'(s)}{\tau(s)}e_3(s)\tag{20}\end{equation}接触球の半径は\begin{equation}R(s)=\sqrt{\rho(s)^2+\left(\frac{\rho'(s)}{\tau(s)}\right)^2}\tag{21}\end{equation}となります。
空間曲線 $c(s)$ が1つの球面上に乗っているためには接触球の中心の位置(20)および半径(21)が $s$ に依存せず一定であればいいです。すなわち微分してゼロということ。(20)を微分したものがゼロであるとすると\begin{equation}\rho(s)\tau(s)+\frac{d}{ds}\left(\frac{\rho'(s)}{\tau(s)}\right)=0\tag{22}\end{equation}が導かれます。(21)でやっても同じ結果となります。よって曲線 $c(s)$ が同一球面上にあるなら(22)が成立します。ちなみにその逆も成立します。地球が完全な球だとすると、地球上で描いた曲線は(22)を満たすわけです。
『幾何学は微分しないと』を参照しました。オヤジギャグまじりの平易な文章で微分幾何学を分かりやすく解説しています。

新装版 幾何学は微分しないと 〜微分幾何学入門〜【Amazon】
次回は曲面論です。
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。