以前に弧長パラメータについて書いた記事を前提知識としています:
弧長パラメータに関する例題が豊富ですので、先に見ておくことをおすすめします。
もくじ
本記事では平面上の曲線のみを扱います。
平面上の曲線は媒介変数 $t$ によって\begin{equation}c(t)=\bigl(x(t),y(t)\bigr)\tag{1}\end{equation}と表せます。物理では主に $t$ を時刻とすることにより、物体の運動の様子が分かります。
$t=t_0$ における微分係数 $c'(t_0)$ を接ベクトルといいます。$t_0$ における曲線の向きをまっすぐな矢印で表したものです。
弧長パラメータ表示とは、端的に言えば接ベクトルの大きさが常に1になるように定めた媒介変数 $s$ によって曲線を表すことであり、$s$ を弧長パラメータといいます。\begin{equation}c(s)=\bigl(x(s),y(s)\bigr)\tag{2}\end{equation}\begin{equation}|c'(s)|=\sqrt{x'(s)^2+y'(s)^2}=1\tag{2}\end{equation}図における意味としては、点 $(x(0),y(0))$ からスタートして、弧長が $s$ となるときの点が $(x(s),y(s))$ である、といえます。以下、基本的には弧長パラメータ表示で話を進めます。具体例は冒頭の前回記事参照。
接ベクトル $c'(s)$ は $s$ における曲線の「1次の近似」すなわち直線による近似です。なので向き(傾き)を表しています。
$c''(s)$ は $c'(s)$ の変化です。$|c'(s)|$ は常に $1$ ですので、変化するのは向きのみです。すなわち $c''(s)$ は「向きの変化」を表します。鋭く曲がれば向きの変化は大きく、$c''(s)$ の大きさは大きくなります。そこで曲率(の大きさ)を\begin{equation}\kappa(s):=|c''(s)|\tag{3}\end{equation}と定めましょう。正負を区別する曲率については後述します。
また、曲線上の点において近似した円の半径によって曲がり具合を表すこともあり、曲率半径といいます。曲線のある1点を思いきり拡大したら直線に見えるというのは、よくある話です。そこで、もう少しズームアウトして点を見つめてみたらどうでしょう?少し曲がっており、円弧の一部に見えそうな気がします。それを完全な円と見立てたときの、その円の半径を曲率半径というわけです。
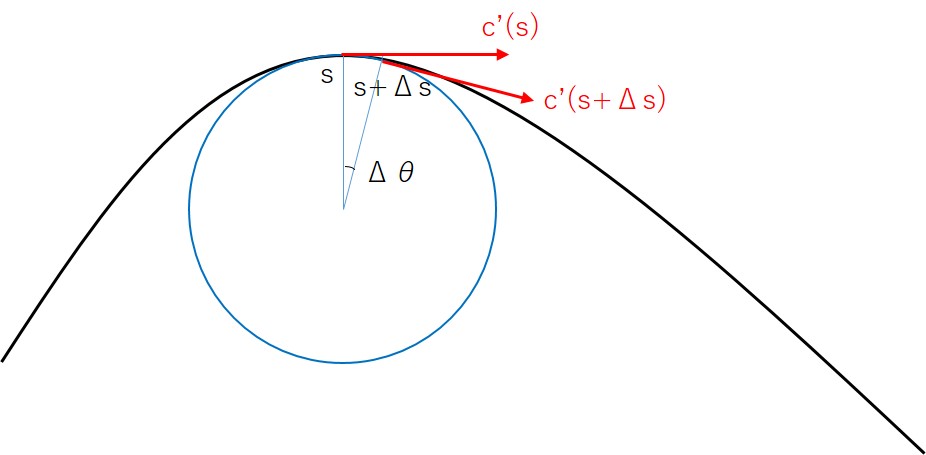
上図のように曲線上の点 $c(s)$ およびそれより少し進んだ $c(s+\Delta s)$ を考えます。弧長パラメータの定義から2点間の弧長は $\Delta s$ です。したがって円の半径を $r(s)$ とすると、$r(s)\Delta\t =\Delta s$ となります。よって曲率半径は\begin{equation}r(s)=\left|\frac{ds}{d\t}\right|\tag{4}\end{equation}と求まります。なお、この $\t$ を「$x$ 軸と接ベクトルがなす角(偏角とよぶことにする)」と定義しても(4)式において問題は起こりません。(4)を導出するにあたっては円の中心角を $\Delta\t$ と定めましたが、初等幾何によって $c'(s)$ の偏角と $c'(s+\Delta s)$ の偏角の差もまた $\Delta\t$ ですから(ただし正負の区別が生まれるので、(4)に絶対値を附した)。
くわえて、微分の定義より成り立つ式$$|c''(s)|=\left|\frac{c'(s+\Delta s)-c'(s)}{\Delta s}\right|$$の右辺の分子について。両者のベクトルはともに大きさ $1$ であり、なす角 $\Delta\t$ ですから、始点をあわせて図形的に考えれば$$|c'(s+\Delta s)-c'(s)|=|c'(s)||\Delta\t|=|\Delta\t|$$\begin{equation}\therefore\quad \kappa(s)=|c''(s)|=\left|\frac{d\t}{d s}\right|\tag{5}\end{equation}となります。
(5)を見ると $\kappa(s)=\dfrac{d\t}{d s}$ と定義してもよいことが分かります。その場合は正負の区別があり、接ベクトルが正方向に回転する場合はプラスです。両辺を積分すると\begin{equation}\int_{s_1}^{s_2}\kappa(s)ds =\t(s_2)-\t(s_1)\tag{6}\end{equation}つまり曲率の積分は、曲線上の2点 $s=s_1,s_2$ 間で接ベクトルの偏角がいくら変化したかに相当します。
したがって、ここからは正負を区別する曲率を使いましょう。\begin{equation}\kappa(s)=\dfrac{d\t}{d s}\tag{7}\end{equation}
列車は曲線の線路上を動いていきます。この列車内で、じっと進行方向を向いて座っているとしましょう。座っている私たちの座標は、上図の接ベクトル $c'(s)$ の方向が $x$ 軸で、それを正方向に $\dfrac{\pi}{2}$ 回転した向きが $y$ 軸みたいになるのではないでしょうか。そしてその座標系は時間とともに動きます。
接ベクトル $\bm{e_1}(s)$ と、正方向に $\dfrac{\pi}{2}$ 回転した法線ベクトル $\bm{e_2}(s)$ は、正規直交基底(直交する単位ベクトルの組)となります。この組を動標構(moving frame)あるいはフレネ標構とよびます。定義より明らかに\begin{equation}\bm{e_1}(s) =\bigl(x'(s),y'(s)\bigr)\tag{8a}\end{equation}\begin{equation}\bm{e_2}(s) =\bigl(-y'(s),x'(s)\bigr)\tag{8b}\end{equation}
このとき曲率を次のように定義することが可能です。\begin{equation}\kappa(s):=\bm{e_1}'(s)\cdot\bm{e_2}(s)\tag{9}\end{equation}具体的に計算する場合は\begin{eqnarray*}\kappa(s) &=& \bigl(x''(s),y''(s)\bigr)\cdot\bigl(-y'(s),x'(s)\bigr)\\&=&x'(s)y''(s)-x''(s)y'(s)\end{eqnarray*}を使うこともできます。さらに $|c'(s)|=1$ より $x'^2+y'^2=1$ なので\begin{eqnarray*}\kappa(s) &=& \frac{x'(s)y''(s)-x''(s)y'(s)}{x'(s)^2+y(s)'^2} \\&=& \frac{d}{ds}\left(\arctan\frac{y'(s)}{x'(s)}\right)\\&=&\frac{d\t}{ds}\end{eqnarray*}これは動標構によって定義した曲率(9)が上述の曲率(7)と等しいことを示しています。
媒介変数が弧長パラメータでない場合について補足します。弧長パラメータ表示における曲率\begin{equation}\kappa(s)=x'(s)y''(s)-x''(s)y'(s)\tag{10}\end{equation}で $s=s(t)$ とします。$t$ についての微分をドットで表すことにすると$$x'(s)=\frac{\dot{x}}{\dot{s}}\;,\;x''(s)=\frac{\ddot{x}}{(\ddot{s})^2}-\frac{\ddot{s}\dot{x}}{(\dot{s})^3}$$$y$ についても同様です。これらを(10)に適用して\begin{equation}\kappa(t)=\frac{\dot{x}\ddot{y}-\ddot{x}\dot{y}}{(\dot{x}^2+\dot{y}^2)^\frac{3}{2}}\tag{11}\end{equation}と求まります。弧長パラメータ表示における式よりも複雑になっています。とはいえ、実際に具体例を計算するときには、弧長パラメータ表示された $x(s)$ と $y(s)$ が複雑な形になりがちなので、$s$ か $t$ のどちらの計算量が多いかというと、明確には分かりません。
$x'^2+y'^2=1$ を微分すると\begin{equation} x'x''+y'y''=0\tag{12}\end{equation}ここで(8a)(10)により\begin{eqnarray*}\kappa\bm{e_1} &=& \bigl((x'y''-x''y')x',(x'y''-x''y')y'\bigr) \\&=& \bigl(x'^2y''-x'x''y',x'y'y''-x''y'^2\bigr) \\&=& \bigl((x'^2+y'^2)y''-y'(x'x''+y'y''),-(x'^2+y'^2)x''+x'(x'x''+y'y'')\bigr) \\&=& \bigl(y'',-x''\bigr)\quad(\because(12))\\&=&-\bm{e_2}'\end{eqnarray*}同様に $\kappa\bm{e_2}$ についても計算します。以上によりフレネ・セレの公式を得ます。
$$\begin{cases}\bm{e_1}'(s) &=& \kappa(s)\bm{e_2}(s)\\\bm{e_2}'(s) &=& -\kappa(s)\bm{e_1}(s)\end{cases}$$あるいは$$\frac{d}{ds}\binom{\bm{e_1}(s)}{\bm{e_2}(s)}=\left(\begin{matrix}0&\kappa(s)\\-\kappa(s)&0\end{matrix}\right)\binom{\bm{e_1}(s)}{\bm{e_2}(s)}$$
特に2つ目の式は、動標構の動きが、反対称行列による動標構の一次変換で表されることを明示しています。
$c(s)=\bigl(x(s),y(s)\bigr)$ を $s=s_0$ まわりに展開すると\begin{equation}c(s)=c(s_0)+(s-s_0)c'(s_0)+\frac{(s-s_0)^2}{2}c''(s_0)+O\bigl((s-s_0)^3\bigr)\tag{13}\end{equation}(8a)およびフレネ・セレの公式から $c'=\bm{e_1}$ , $c''=\kappa\bm{e_2}$ ですので\begin{equation}c(s)=c(s_0)+(s-s_0)\bm{e_1}(s_0)+\frac{(s-s_0)^2}{2}\kappa(s_0)\bm{e_2}(s_0)+O\bigl((s-s_0)^3\bigr)\tag{14}\end{equation}これが曲線の2次までの近似式となります。曲率は2次の項に現れています。
ここまでは曲線が存在する場合に、微分によって曲率を求めるという話をしていました。今度は逆に、先に連続関数 $\kappa(s)$ がある場合に、$\kappa(s)$ を曲率とするような曲線が存在することを示しましょう。
いま $\kappa(s)$ に対し、$$c(s):=\int_0^s\left(\cos K(t),\sin K(t)\right)dt\;,\quad K(t):=\int_0^t\kappa(u)du$$と定めます。このとき$$c'(s)=\left(\cos K(s),\sin K(s)\right)\;,\; c''(s)=\left(-K'(s)\sin K(s),K'(s)\cos K(s)\right)$$$$\therefore\quad |c'(s)|=1\;,\; x'(s)y''(s)-x''(s)y'(s)=\kappa(s)$$接ベクトルの大きさが常に $1$ なので $s$ は弧長パラメータになっていますし、曲率は $\kappa(s)$ になっています。よって曲率が与えられれば、対応する曲線が存在するのです。
しかも曲率が定まっているとき、曲線はただ1つに決定します。ただし決定するのは曲線の形であって、回転と平行移動という自由度はあります。
曲率を $\kappa(s)$ とする平面曲線は、回転と平行移動によって一致するものを除いて、だた1つである。
【証明】曲率 $\kappa(s)$ である曲線 $c_A(s)$ , $c_B(s)$ を考える。これらを縦ベクトルとする。それぞれの動標構を $e_1^A(s),e_2^A(s)$ および $e_1^B(s),e_2^B(s)$ と書き、次の行列を定める。$$X_A(s)=\left(\begin{matrix}e_1^A(s)&e_2^A(s)\end{matrix}\right)=\left(\begin{matrix}x'_A(s)& -y'_A(s)\\y'_A(s)& x'_A(s)\end{matrix}\right)$$$$X_B(s)=\left(\begin{matrix}e_1^B(s)&e_2^B(s)\end{matrix}\right)=\left(\begin{matrix}x'_B(s)& -y'_B(s)\\y'_B(s)& x'_B(s)\end{matrix}\right)$$2つの曲線は、回転と平行移動によって $s=0$ における位置および接ベクトルの向きを合わせることができるから$$c_A(0)=c_B(0)\;,\;c'_A(0)=c'_B(0)$$すなわち$$X_A(0)=X_B(0)$$また、簡単な計算により$${}^tX_A(s)X_A(s)={}^tX_B(s)X_B(s)=I$$さらにフレネ・セレの公式より\begin{eqnarray*}X_A'(s) &=&\left(\begin{matrix}\left(e_1^A(s)\right)'&\left(e_2^A(s)\right)'\end{matrix}\right) \\&=& \left(\begin{matrix}\kappa e_2^A(s)& -\kappa e_1^A(s)\end{matrix}\right) \\&=& X_A(s)K(s)\end{eqnarray*}ただし$$K(s):=\left(\begin{matrix}0& -\kappa(s)\\\kappa(s)& 0\end{matrix}\right)$$である。$ X_B(s)$ についても同様。すると\begin{eqnarray*}\left(X_A{}^t\!X_B\right)' &=& X_A'{}^t\!X_B+X_A'\left({}^t\!X_B\right)' \\&=& X_AK{}^t\!X_B+X_A{}^t\!(X_BK)\\&=& X_AK{}^t\!X_B+X_A{}^t\!K{}^t\!X_B \\&=& X_A(K+{}^t\!K)X_B\\&=& 0\quad(\because K=-{}^t\!K)\end{eqnarray*}$$\therefore\quad X_A(s){}^t\!X_B(s)=X_A(0){}^t\!X_B(0)=const.$$したがって、$(X_B(s))^{-1}=^t\!X_B(s)$ であることに注意して\begin{eqnarray*}X_A(s)\left(X_B(s)\right)^{-1} &=& X_A(s) ^t\!X_B(s) = X_A(0) ^t\!X_B(0) \\&=& X_A(0) \left(X_B(0)\right)^{-1} = X_A(0) \left(X_A(0)\right)^{-1}\\&=&I\end{eqnarray*}$$\therefore\quad X_A(s)=X_B(s)$$これで $c_A'(s)=c_B'(s)$ が示された。よって$$c_A(s)=c_B(s)$$【証明終】
半径 $4$ の円の弧長パラメータ表示:$$c(s)=\left( -4\cos\frac{s}{4}\;,\; -4\sin\frac{s}{4}\right)$$において、
(1) $c'(s)$ と $c''(s)$ を計算せよ。
(2) 動標構 $\bm{e_1}(s)$ , $\bm{e_2}(s)$ を求めよ。
(3) 曲率を計算せよ(正負あり)。曲率半径はいくらか。
(4) 弧長パラメータが $4\pi$ 進んだときの接ベクトルの偏角の変化量を求めよ。
【解答】$c'(s)=( \sin\frac{s}{4}\;,\; -\cos\frac{s}{4})$ , $c''(s)=( \frac{1}{4}\cos\frac{s}{4}\;,\;\frac{1}{4}\sin\frac{s}{4})$ である。よって(8a)(8b)より$$\bm{e_1}(s)=\left( \sin\frac{s}{4}\;,\; -\cos\frac{s}{4}\right)$$$$\bm{e_2}(s)=\left(\cos\frac{s}{4}\;,\;\sin\frac{s}{4}\right)$$(9)によって曲率は $\kappa(s)=1/4$ , その逆数は曲率半径 $r(s)=4$ .
(6)式を用いると$$\t(s+4\pi)-\t(s)=\int_{s}^{s+4\pi}\kappa(s)ds=\pi $$よって $\pi$ ラジアン回る。
【解答終】
双曲線の弧長パラメータ表示 \begin{equation}\begin{cases}x(s)&=&\log(s+\sqrt{s^2+1})\\y(s)&=&\sqrt{s^2+1}\end{cases}\end{equation}において、
(1) $c'(s)$ と $c''(s)$ を計算せよ。
(2) 動標構 $\bm{e_1}(s)$ , $\bm{e_2}(s)$ を求めよ。
(3) 曲率を計算せよ。
【略解】微分した結果や曲率はこちらを参照。最終的に$$\kappa(s)=\frac{1}{s^2+1}$$【解答終】
サイクロイドの弧長パラメータ表示\begin{equation}c(s)=\left(2\arccos(1-\frac{s}{4})-\frac{4-s}{8}\sqrt{s(8-s)},s-\frac{s^2}{8} \right)\end{equation}において、
(1) $c'(s)$ と $c''(s)$ を計算せよ。
(2) 動標構 $\bm{e_1}(s)$ , $\bm{e_2}(s)$ を求めよ。
(3) 曲率を計算せよ。
【略解】\begin{equation}c^\prime(s)=\left(\frac{1}{4}\sqrt{8s-s^2},1-\frac{s}{4}\right)\end{equation}\begin{equation}c^{\prime\prime}(s)=\left(\frac{4-s}{4\sqrt{8s-s^2}},-\frac{1}{4}\right)\end{equation}曲率は\begin{equation}\kappa(s)=\frac{1}{\sqrt{s(8-s)}}\end{equation}【解答終】
曲率が恒等的にゼロとなる曲線は、直線であることを示せ。
【解答】フレネ・セレの公式より $\kappa(s)=0$ ならば $\bm{e_1}'(s)=\bm{e_2}'(s)=0$. よって $\bm{e_1}(s)$ は定数ベクトル $\bm{a}$ と書ける。よって $c'(s)=\bm{a}$ なので$$c(s)=s\bm{a}+\bm{b}$$と書ける。これは直線を表す。
【解答終】
曲率を一定割合で変化させていった場合に描かれる軌跡をクロソイド曲線という。クロソイドは道路の設計にも用いられており、自動車であればハンドルを滑らかに等速回転させて安全に走行できるとされる。
定数 $a$ に対し、クロソイドの曲率を $as$ としよう。このときの曲線を弧長パラメータ表示せよ。
【解答】$\kappa(s)=as$ と(6)より$$\t(s)=\int_0^s \kappa(t)dt=\frac{a}{2}s^2$$ただし $\t(s)$ は接ベクトル $c'(s)$ の偏角であり、初期条件として $\t(0)=0$ とした。すなわち$$c'(s)=\left(\cos\frac{a}{2}s^2,\sin\frac{a}{2}s^2\right)$$である。これを積分すると曲線の弧長パラメータ表示を得るが、これはフレネル積分といわれ、初期条件 $c(0)=(0,0)$ とすれば\begin{eqnarray*}c(s)&=&\left(\sqrt{\frac{2}{a}}\int_0^{s\sqrt{\frac{a}{2}}}\cos u^2du,\sqrt{\frac{2}{a}}\int_0^{s\sqrt{\frac{a}{2}}}\sin u^2du\right)\\&=&\sqrt{\frac{2}{a}}\left(C\left(s\sqrt{\frac{a}{2}}\right),S\left(s\sqrt{\frac{a}{2}}\right)\right)\end{eqnarray*}【解答終】
『幾何学は微分しないと』を参照しました。オヤジギャグまじりの平易な文章で。微分幾何学を分かりやすく解説しています。

新装版 幾何学は微分しないと 〜微分幾何学入門〜【Amazon】
次回は空間曲線です:
空間曲線1-弧長パラメータと動標構、曲率・捩率、フレネ・セレの公式
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。