微分幾何学の講座・第3回。前回の平面曲線に引き続き、空間における曲線の弧長パラメータ表示、動く座標系「動標構」と曲率を求めます。また動標構の変化を定めるフレネ・セレの公式を導出します。
前回はこちらから:
弧長パラメータと動標構、曲率、フレネ・セレの公式【平面曲線】
もくじ
空間曲線は媒介変数 $t$ によって\begin{equation}c(t)=\bigl(x(t),y(t),z(t)\bigr)\tag{1}\end{equation}と表せます。物理では主に $t$ を時刻とすることにより、物体の運動の様子を表現することが多いです。ここでは、ベクトルの上に矢印をつけたり太字にはしないことにします。
$t=t_0$ における微分係数 $c'(t_0)$ を接ベクトルといいます。$t_0$ における曲線の向きをまっすぐな矢印で表したものです。ここでは $c'(t)\neq 0$ すなわち $(x',y')\neq 0$ としておきます。そうでないと $c(t)$ は1点から動かないことになってしまい、本記事での内容にそぐわないからです。
これまでにも見たように、端的に言えば接ベクトルの大きさが常に1になるように定めた媒介変数 $s$ (弧長パラメータ)によって曲線を表すことを「弧長パラメータ表示」といいます。\begin{equation}c(s)=\bigl(x(s),y(s),z(s)\bigr)\tag{2}\end{equation}\begin{equation}|c'(s)|=\sqrt{x'(s)^2+y'(s)^2+z'(s)^2}=1\tag{3}\end{equation}図における意味としては、点 $(x(0),y(0),z(0))$ からスタートして、弧長が $s$ となるときの点が $(x(s),y(s),z(s))$ である、といえます。先ほど $c'(t)\neq 0$ を仮定した理由が(3)からも分かります。
実際に曲線の弧長パラメータ表示を求める例題は後ほど取り上げます。
以下、訳あって\begin{equation}c''(s)\neq0\tag{4}\end{equation}を仮定しておきます。すなわち直線を排除します。
平面曲線のときは単位接ベクトル $e_1(s)$ とそれを $\frac{\pi}{2}$ 回転させた単位法線ベクトル $e_2(s)$ の組を動標構(moving frame)あるいはフレネ標構とよぶのでした。これは曲線に沿って変化する「動く座標系」であり、線路を進む列車内で座っている人から見た座標のようでもあります。また、2つのベクトルは正規直交基底(直交する単位ベクトルの組)となっているのでした。
同様に空間曲線における動標構は3つの正規直交基底によって得られます。すなわち、単位接ベクトル $e_1(s)$、単位主法線ベクトル $e_2(s)$、そして単位従法線ベクトル $e_3(s)$ です。
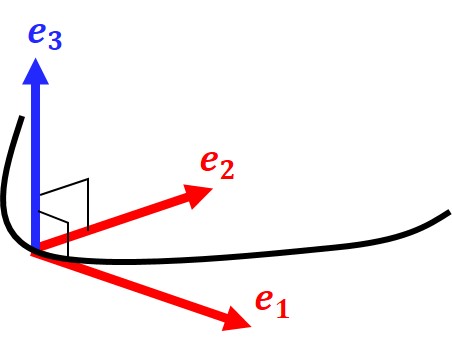
接ベクトル $e_1(s)$ は平面曲線のときと同じく、曲線に接する方向(物理でいう速度の向き)を向いています。すなわち位置ベクトルの微分ですから $e_1(s)=c'(s)$ です。
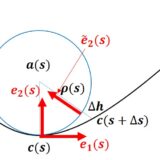
問題はそれと直交する法線です。空間曲線を想像すると、接ベクトルと垂直なベクトルは無数にあることが分かります。そこで、$e_1(s)$ と $e_1(s+\Delta s)$ が乗る平面(接触平面という)を考えたとき(下図)、近似される円の中心を向く法線ベクトルを主法線ベクトル $e_2$ と定めます。
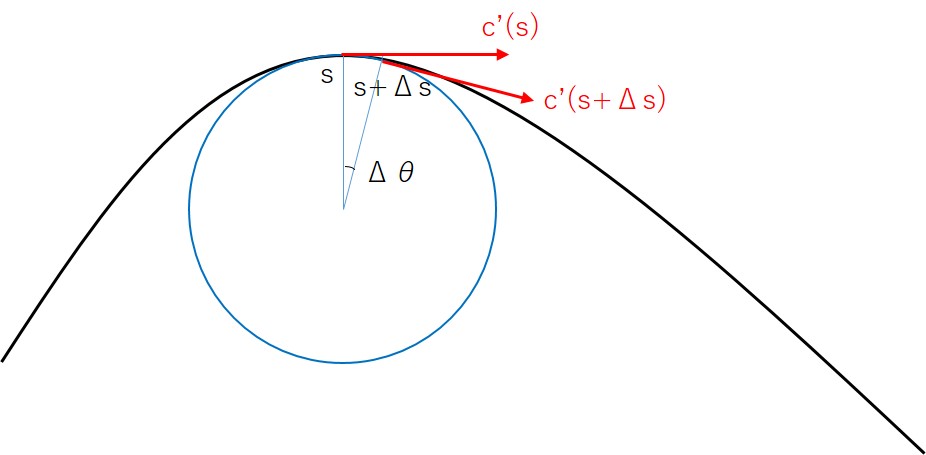
$c'(s)$ の変化 $c'(s+\Delta s)-c'(s)$ は円の中心を向いています(平面と同じ)。したがって $e_2(s)$ は $c''(s)$ と同じ向きの単位ベクトルといえます。
なお、接ベクトル $e_1$ と主法線ベクトル $e_2$ が乗る平面は接触平面です。
最後に、上図のように $e_3(s)$ を $e_1(s)$ と $e_2(s)$ の外積で定義すれば正規直交基底を作れます。
以上により、定義として次のように書けます。
曲線 $c(s)$ における動標構は以下で定める単位接ベクトル $e_1(s)$、単位主法線ベクトル $e_2(s)$、単位従法線ベクトル $e_3(s)$ の組である。\begin{eqnarray}e_1(s)&:=&c'(s)\tag{5} \\ e_2(s) &:=& \frac{c''(s)}{|c''(s)|}\tag{6} \\ e_3(s)&:=&e_1(s)\times e_2(s)\tag{7}\end{eqnarray}
(4)の仮定は(6)を定義するためにあります。(5)(6)(7)の定義から $e_1(s)$ , $e_2(s)$ , $e_3(s)$ が正規直交基底をなすことを示すこともできますので、やってみてください(ヒント:(3)を微分する)。
$c''(s)$ は $c'(s)$ の変化です。$|c'(s)|$ は常に $1$ なので、変化するのは向きのみです。すなわち $c''(s)$ は「向きの変化」を表します。鋭く曲がれば向きの変化は大きく、$c''(s)$ の大きさは大きくなります。つまり曲率は\begin{equation}\kappa(s)=|c''(s)|\tag{8}\end{equation}と考えてよいです。動標構によって定義するなら次のようになります。
\begin{equation}\kappa(s)=e_1'(s)\cdot e_2(s)\tag{9}\end{equation}
この定義と(5)(6)よりただちに(8)または\begin{equation}\kappa(s)=|e'_1(s)|\tag{10}\end{equation}を得ます。(9)の定義は平面曲線のときと同じ式です。ただし平面曲線の曲率に正負があったのに対し、空間曲線の曲率は常に正である点は異なります。平面曲線では常に、接ベクトルを正方向に $\pi/2$ 回転させたものを $e_2(s)$ と定めることにより、$e_2(s)$ の方向は曲率中心またはその逆向きがあり得たためです。
本記事では基本的に $c''(s)\neq 0$ を仮定していましたが、$c''(s)=0$ (直線)の場合は(8)式によって $\kappa(s)=0$ と定めることができます。これは、直線は曲がっていない、すなわち曲率ゼロということです。曲率はゼロであれば直線であり、大きくなるほど線はグニャリと大きく曲がっているというわけです。
$e_3(s)$ の大きさは常に1ですので、$e_3(s)$ は変化するとしても向きだけです。
もし空間曲線が $xy$ 平面上のみを動くならば、$e_3(s)$ はずっと $z$ 方向を向いていて不変です。もう少し一般的に言えば、曲線が同一平面上のみにあるなら(接触平面が変化しないなら)、 $e_3(s)$ は不変です。
しかし曲線が「捩れ」ていて、接触平面が変化する場合、捩れが大きいほど $e_3(s)$ も大きく変化します。これを表すものが捩率(torsion)です。捩率は、パラメータが $s$ から $s+\Delta s$ まで進む間に接触平面が何ラジアン傾いたかを示す量です。要は $s$ での接触平面と $s+\Delta s$ での接触平面のなす角ということですが、2平面のなす角は法線どうしのなす角に等しいので、$e_3(s)$ と $e_3(s+\Delta s)$ のなす角 $\Delta\t$ を考えればよいです(下図)。ただし図2の $\t$ とは無関係です。
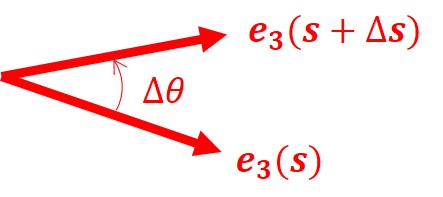
図3よりただちに$$2\left|\sin\frac{\D\t}{2}\right|=|e_3(s+\D s)-e_3(s)|$$両辺を $\D s$ で割って $\D s\to0$ の極限をとると\begin{equation}\left|\frac{d\t}{ds}\right|=|e_3'(s)|\tag{11}\end{equation}これが捩率 $\tau(s)$ の大きさであり、\begin{equation}\left|\tau(s)\right|=|e_3'(s)|\tag{12}\end{equation}となります(後述するが、実際には捩率には正負がある)。
このように捩率はゼロであれば平面曲線であり、(絶対値が)大きくなるほど平面から大きく離れていることを表すのだとイメージできます。
ただし捩率の定義は(9)と同様にやや天下り的であり、次のようになります。
\begin{equation}\tau(s)=e_2'(s)\cdot e_3(s)\tag{13}\end{equation}
後述のフレネ・セレの公式を使えば、(13)から(12)を瞬時に示すことができます。
これらより導かれる系として
$$\kappa(s)=|c''(s)|\;,\;\tau(s)=\frac{\mathrm{det}\left(c'(s),c''(s),c'''(s)\right)}{|c''(s)|^2}$$
左側の式は先ほど出てきました。$\tau$ のほうはベクトル三重積が3×3の行列式で表せることから\begin{eqnarray*}\tau(s) &=&e_2'(s)\cdot e_3(s) \\&=& e_2'(s)\cdot \left(e_1(s)\times e_2(s)\right) \\&=& \mathrm{det}\left(e_1(s),e_2(s),e'_2(s)\right) \\&=& \mathrm{det}\left(c'(s),\frac{c''(s)}{|c''(s)|},\frac{d}{ds}\frac{c''(s)}{|c''(s)|}\right)\\&=&\mathrm{det}\left(c'(s),\frac{c''(s)}{|c''(s)|},\frac{c'''(s)}{|c''(s)|}+c''(s)\frac{d}{ds}\frac{1}{|c''(s)|}\right)\\&=& \mathrm{det}\left(c'(s),\frac{c''(s)}{|c''(s)|},\frac{c'''(s)}{|c''(s)|}\right)\\&=&\frac{\mathrm{det}\left(c'(s),c''(s),c'''(s)\right)}{|c''(s)|^2} \end{eqnarray*}と導出できます。なお途中、$\mathrm{det}(a,b,c+d)=\mathrm{det}(a,b,c)+\mathrm{det}(a,b,d)$ および $\mathrm{det}(a,b,b)=0$ を使いました。これらは行列式の基本的な性質です。
ここまでの内容に関して具体例を見ていきましょう。
空間内の円 $c(s)=(\frac{1}{2}\cos 2s , \frac{1}{2}\sin 2s , 1)$ について、
(1)動標構(3つの基本ベクトル)を求めよ。
(2)定義から曲率と捩率を求めよ。
【解答】単位接ベクトルは$$e_1(s)=c'(s)=(-\sin 2s,\cos 2s,0)$$さらに微分して$$c''(s)=(-2\cos 2s,-2\sin2s,0)$$ですから$$e_2(s)=(-\cos2s,-\sin2s,0)$$$e_1(s)$ と $e_2(s)$ の外積をとって$$e_3(s)=(0,0,1)$$これらより曲率と捩率は$$\kappa(s)=2\;,\;\tau(s)=0$$これは平面曲線なので捩率がゼロになっていますね。【解答終】
$a,b>0$ に対し、常螺旋$$c(t)=(a\cos t,a\sin t,bt)$$を定義する。このとき、
(1)この曲線を弧長パラメータ表示せよ。
(2)動標構を求めよ。
(3)曲率と捩率を求めよ。
【解答】過去記事のように弧長パラメータ表示を求める。$$s(t)=\int_0^t |c(t)|dt=\sqrt{a^2+b^2}\;t$$$$\therefore \quad t(s)=\frac{s}{\sqrt{a^2+b^2}}$$よって弧長パラメータ表示は$$c(s)=\left(a\cos \frac{s}{\sqrt{a^2+b^2}},\,a\sin\frac{s}{\sqrt{a^2+b^2}},\,\frac{bs}{\sqrt{a^2+b^2}}\right)$$微分して$$e_1(s)=\frac{1}{\sqrt{a^2+b^2}}\left(-a\sin \frac{s}{\sqrt{a^2+b^2}},\,a\cos\frac{s}{\sqrt{a^2+b^2}},\,b\right)$$(6)を用いて$$e_2(s)=\left(-\cos \frac{s}{\sqrt{a^2+b^2}},\,-\sin\frac{s}{\sqrt{a^2+b^2}},\,0\right)$$(7)により$$e_3(s)=\frac{1}{\sqrt{a^2+b^2}}\left(b\sin \frac{s}{\sqrt{a^2+b^2}},\,-b\cos\frac{s}{\sqrt{a^2+b^2}},\,a\right)$$(9)(13)から$$\kappa(s)=\frac{a}{a^2+b^2}\;,\;\tau(s)=\frac{b}{a^2+b^2}$$【解答終】
前回、平面曲線に関するフレネ・セレの公式を導出しました。フレネ・セレの公式は動標構の変化(微分)を明示する式です。空間でもやってみましょう。
まず $e_1(s)$ の微分は$$e'_1(s)=c''(s)=|c''(s)|e_2(s)\quad(\because(6))$$さらに(8)より\begin{equation}e'_1(s)=\kappa(s)e_2(s)\tag{14}\end{equation}
動標構をなす3つのベクトル $e_1$ , $e_2$ , $e_3$ は大きさ1でした。よって2乗したものを微分するとゼロなので\begin{equation}e_1(s)\cdot e'_1(s)=e_2(s)\cdot e'_2(s)=e_3(s)\cdot e'_3(s)=0\tag{15}\end{equation}が成り立ちます。つまりそれぞれのベクトルは、自身の微分と直交するのです。よって $e'_2(s)$ は $s$ に応じて定まる数 $a,b$ を用いて\begin{equation}e'_2(s)=ae_1(s)+be_3(s)\tag{16}\end{equation}とできます。すると\begin{eqnarray*}e_1(s)\cdot e_2(s)=0 &\Rightarrow& e'_1(s)\cdot e_2(s)+e_1(s)\cdot e'_2(s)=0\\ &\Rightarrow& \kappa(s)+e_1(s)\cdot \{ae_1(s)+be_3(s)\}=0\quad(\because(9)(16))\\&\Rightarrow& \kappa(s)+a=0\end{eqnarray*}\begin{equation}\therefore\quad a=-\kappa(s)\tag{17}\end{equation}さらに\begin{eqnarray*}e_2(s)\cdot e_3(s)=0 &\Rightarrow& e'_2(s)\cdot e_3(s)+e_2(s)\cdot e'_3(s)=0\\ &\Rightarrow& \tau(s)+e_2(s)\cdot e'_3(s)=0\quad(\because(13))\end{eqnarray*}\begin{equation}\therefore\quad e_2(s)\cdot e'_3(s)=-\tau(s)\tag{18}\end{equation}これについては一方で(7)より\begin{eqnarray}e'_3(s) &=& e'_1(s)\times e_2(s)+ e_1(s)\times e'_2(s) \\&=& \kappa(s)e_2(s)\times e_2(s)+e_1(s)\times\{ae_1(s)+be_3(s)\}\quad(\because(14)(16)) \\&=& b e_1(s)\times e_3(s) \\&=& -b e_2(s)\tag{19}\end{eqnarray}この両辺と $e_2(s)$ との内積を考えると\begin{equation}\therefore\quad e_2(s)\cdot e'_3(s)=-b\tag{20}\end{equation}(18)(20)より\begin{equation}\therefore\quad b=\tau(s)\tag{21}\end{equation}(17)(21)を(16)(19)に適用します。(14)もセットにして次の最終形ができあがります。
\begin{equation}\frac{d}{ds}\begin{pmatrix}e_1(s)\\e_2(s)\\e_3(s)\end{pmatrix}=\begin{pmatrix}0 & \kappa(s) & 0\\-\kappa(s) & 0 & \tau(s)\\0 & -\tau(s) & 0\end{pmatrix}\begin{pmatrix}e_1(s)\\e_2(s)\\e_3(s)\end{pmatrix}\tag{22}\end{equation}
とてもきれいな公式です。
空間曲線 $c(s)$ を $s=s_0$ まわりに展開すると$$c(s)=c(s_0)+(s-s_0)c'(s_0)+\frac{(s-s_0)^2}{2}c''(s_0)+\frac{(s-s_0)^3}{6}c'''(s_0)+O\bigl((s-s_0)^4\bigr)$$フレネ・セレの公式より$$c'=e_1\;,\;c''=\kappa e_2\;,\; c'''=\kappa' e_2-\kappa^2 e_1+\kappa\tau e_3$$したがって
\begin{eqnarray}c(s) &=& c(s_0)+(s-s_0)e_1(s_0)+\frac{(s-s_0)^2}{2}\kappa(s_0)e_2(s_0)\\&&+\frac{(s-s_0)^3}{6}\left\{-\kappa^2(s_0) e_1(s_0)+\kappa'(s_0) e_2(s_0)+\kappa(s_0)\tau(s_0) e_3(s_0)\right\}\\&&+O\bigl((s-s_0)^4\bigr)\tag{23}\end{eqnarray}
$s-s_0$ に関して昇べきに並べていますが、動標構 $e_1$ , $e_2$ , $e_3$ について整理して書くこともあります。
$c(s)$ における接線に $c(s+\D s)$ から下ろした垂線の足の長さを $\D h$ とするとき$$\lim_{\D s\to0}\frac{\D h}{(\D s)^2}=\frac{\kappa(s)}{2}$$を示せ。
【略解】図を書けば、$c(s+\D s)-c(s)$ を $e_2(s)$ に正射影したものの長さが $\D h$ です。$$\D h=(c(s+\D s)-c(s))\cdot e_2(s)$$ブーケの公式を用いて$$=\frac{\kappa(s)}{2}(\D s)^2+O(\D s^3)$$あとは式を整理する。【終】
曲率が「直線とどれだけ離れているか」を表すことの、幾何学的なイメージを語る1つです。
平面曲線の場合、曲率が定まっていれば曲線の形はただ1つに決まるのでした。空間曲線の場合は次のようになります。
関数 $\kappa(s)>0$ および $\tau(s)$ が定まっているとき、$s$ を弧長パラメータとして曲率 $\kappa(s)$、捩率 $\tau(s)$ をもつ曲線 $c(s)$ が、回転と平行移動の自由度を除いて一意的に存在する。
証明は省きます。
多くの曲線ではそもそも弧長パラメータ表示ができないことが多いです。一般のパラメータ $t$ に対して、曲線 $c(t)$ の曲率および捩率は次の式で表されます。
\begin{equation}\kappa(t)=\frac{|\dot{c}(t)\times \ddot{c}(t)|}{|\dot{c}(t)|^3}\tag{24}\end{equation}\begin{equation}\tau(t)=\frac{\mathrm{det}(\dot{c}(t),\ddot{c}(t),\dddot{c}(t))}{|\dot{c}(t)\times\ddot{c}(t)|^2}\tag{25}\end{equation}
計算が少々面倒ですが、ここでは概略にとどめます。定理1からスタートして $s=s(t)$ と置換します。その際\begin{eqnarray*}c'(s)&=&\frac{\dot{c}(t)}{|\dot{c}(t)|}\\c''(s)&=&\frac{1}{|\ddot{c}(t)|^2}\left[\ddot{c}(t)-\frac{\dot{c}(t)\cdot\ddot{c}(t)}{|\dot{c}(t)|^2}\dot{c}(t)\right]\end{eqnarray*}および$$c'''(s)=\dddot{c}(t)t'(s)^3+3\ddot{c}(t)t''(s)t'(s)+\dot{c}(t)t'''(s)$$を代入することから始めます。特に(25)の証明では定理1を示したときと同様、行列式の性質を用いてスマートに計算します。また$$\sqrt{|\dot{c}(t)|^2|\ddot{c}(t)|^2-(\dot{c}(t)\cdot\ddot{c}(t))^2}=|\dot{c}(t)||\ddot{c}(t)|\sin\t=|\dot{c}(t)\times\ddot{c}(t)|$$も使います(ラグランジュ恒等式)。$\t$ は $\dot{c}(t)$ と $\ddot{c}(t)$ のなす角です。
『幾何学は微分しないと』を参照しました。オヤジギャグまじりの平易な文章で微分幾何学を分かりやすく解説しています。

新装版 幾何学は微分しないと 〜微分幾何学入門〜【Amazon】
次:
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。