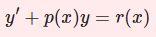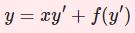１階の非線型な微分方程式の一種であるベルヌーイの微分方程式を、例題つきで紹介します。非線型でありながらも、適切な変形を施すことで非斉次１階線型微分方程式へ帰着する例です。
非斉次１階線型微分方程式の解法については過去記事
【D1】１階線型微分方程式の解法
をご覧ください。
$$y^\prime+p(x)y=q(x)y^a\;,\;a\neq 0,1$$
ベルヌーイ方程式は非線型の微分方程式ながら、適切な変形を施すことで非斉次な１階線型微分方程式へ帰着させ、厳密解を得られるというものです。
$a$ は実数ですが $0,1$ ではありません。もし $a=0,1$ なら非斉次１階線型微分方程式そのものですので特別に論じる必要はありませんから。
$u(x)\equiv y^{1-a}$ として微分することにより$$y' =\frac{1}{1-a}y^au'$$なる関係式を得ます。ベルヌーイ方程式の第1項にこの関係式を代入、さらに $uy^{-(1-a)}=1$ を第2項にかけることで$$\frac{1}{1-a}y^au^\prime+puy^a=qy^a \Longleftrightarrow u^\prime+(1-a)p(x)u=(1-a)q(x)$$これで $u(x)$ に関する非斉次１階線型微分方程式となりました。あとはこれを解けば $y$ も得られるというわけです。
最後の式を丸暗記するのではなく、「$u(x)\equiv y^{1-a}$ とおく」ということだけ覚えて、あとは方程式にある $y$ を $u$ へ置き換えていくというごく当然の手法を進めればいいと思います。
$y'+2y=y^2$ を解け．
$u(x)=y^{-1}$ とおき、微分すると $y'=-y^2u'=-u^{-2}u'$ を得ます。これにより与方程式は$$-u^{-2}u'+2u^{-1}=u^{-2}$$となります。$u^2$ をかけて整理すると$$u^\prime-2u=-1$$となります。変数分離によってこれを解くと $u=\displaystyle\frac{1}{2}(Ce^{2x}+1)$となります。$$\therefore \;y(x)=\frac{2}{Ce^{2x}+1}$$
$u(x)=y^{-1}$ とおくのは技巧的ですが、それ以外は基本的な式変形であることを確認してください。
$y^\prime+\displaystyle\frac{y}{3}=\frac{1-2x}{3}y^4$ を解け。
$u(x)=y^{-3}$ とおき、微分すると$$y'=-\frac{1}{3}y^4u'=-\frac{1}{3}u^{-\frac{4}{3}}u'$$ を得ます。これにより与えられた方程式は$$-\frac{1}{3}u^{-\frac{4}{3}}u'+\frac{1}{3}u^{-\frac{1}{3}}=\frac{1-2x}{3}u^{-\frac{4}{3}}$$$$\therefore\;u'-u=2x-1$$
これは非斉次１階微分方程式です。以下のように解きます。\begin{eqnarray*}& &u'e^{-x}-ue^{-x}=(2x-1)e^{-x}\\ &\Longleftrightarrow &(ue^{-x})'=(2x-1)e^{-x}\\ &\Longleftrightarrow & ue^{-x}=-e^{-x}(2x+1)+C\\ &\Longleftrightarrow & u=Ce^x-2x-1\\ &\therefore & y=(Ce^{x}-2x-1)^{-\frac{1}{3}}\end{eqnarray*}
生態学における個体群成長モデルの１つであるロジスティック方程式$$\frac{dN}{dt}=r\left(1-\frac{N}{K}\right)N\quad (r,K>0)$$を解け。初期条件を $N(0)=N_0$ とする。また $N(\infty)$ の値はどうなるか。
定数 $r$ を内的自然増加率といい、簡単に言うとその生物の繁殖力である。定数 $K$ を環境収容力といい、その生物が継続して繁栄できる最大の個体数である。
やってみてください。まぁこれは変数分離でも解けてしまうのですが・・・。
次回：
【D3】クレローの方程式と包絡線（解法と例題）
【D4】Chrystalの微分方程式と包絡線
本記事では、下記の本を大いに参考にしています。厳密性はほどほどに、なるべくたくさんの演習問題が用意されています。産業や自然界における事例も豊富。数学科以外の理学部・工学部生にオススメです。
【Amazon】常微分方程式 (技術者のための高等数学)
Please support me!
記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。