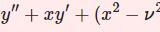\begin{equation}(t^2+pt+q)\frac{d^2y}{dt^2}+(rt+s)\frac{dy}{dt}+Ky=0\tag{1}\end{equation}
2階の係数に2次式が,1階の係数に1次式がついている方程式です.これは適切な変換によりガウスの超幾何微分方程式に書き直せます.
ガウスの超幾何微分方程式については
$t^2+pt+q=0$ の解を $t_1,t_2$ とし$$x\equiv \frac{t-t_1}{t_2-t_1}$$なる変換をします.すると上記方程式は $y(x)$ に関する微分方程式$$x(1-x)y''+\left[ -\frac{rt_1+s}{t_2-t_1}-rx \right]y'-Ky=0$$となります.$K=ab$ , $r=a+b+1$ , $rt_1+s=c(t_2-t_1)$ とすれば超幾何微分方程式に帰着できたことが分かります.
ガウスの超幾何微分方程式は$$x(1-x)y^{\prime\prime}+[c-(a+b+1)x]y'-aby=0$$であり,2つの特殊解は$$F(a,b,c;x)\;,\;x^{1-c}F(a-c+1,b-c+1,2-c;x)$$
$(t^2-5t+6)\dfrac{d^2y}{dt^2}+(1-2t)\dfrac{dy}{dt}-2y=0$ を超幾何微分方程式に帰着させよ.
変形すると$$(t-2)(t-3)\frac{d^2y}{dt^2}+(1-2t)\frac{dy}{dt}-2y=0$$2階導関数の係数 $(t-2)(t-3)$ より $x\equiv\displaystyle\frac{t-2}{3-2}=t-2$ とおきます。$dx=dt$ より微分方程式を変形すると $y(x)$ についての方程式$$x(1-x)y^{\prime\prime}+(3+2x)y'+2y=0$$を得ます.
超幾何微分方程式 $x(1-x)y^{\prime\prime}+[c-(a+b+1)x]y'-aby=0$ の2つの特殊解は$$F(a,b,c;x)\;,\;x^{1-c}F(a-c+1,b-c+1,2-c;x)$$です。この事実と比べると$$c=3\;,\;a=\frac{-3+\sqrt{17}}{2}\;,\;b=-\frac{3+\sqrt{17}}{2}$$ですから2つの特殊解は\begin{eqnarray*}y_1 &=& F\left(\frac{-3+\sqrt{17}}{2},-\frac{3+\sqrt{17}}{2},3;x\right)\\ y_2 &=& \frac{1}{x^2}F\left(\frac{-7+\sqrt{17}}{2},-\frac{7+\sqrt{17}}{2},-1;x\right)\end{eqnarray*}となります.多分ここまでしか進めないと思います.
$(t^2-5t+6)\displaystyle\frac{d^2y}{dt^2}+(1-2t)\frac{dy}{dt}+2y=0$ を解け.
先の例題と1か所の符号が違うだけです.同様に $x\equiv\displaystyle\frac{t-2}{3-2}=t-2$ とおきます.$dx=dt$ より微分方程式を変形すると $y(x)$ についての方程式$$x(1-x)y^{\prime\prime}+(3+2x)y'-2y=0$$を得ます.
超幾何微分方程式 $x(1-x)y^{\prime\prime}+[c-(a+b+1)x]y'-aby=0$ と比べて$$a=-1\;,\;b=-2\;,\;c=3$$1つ目の特殊解は\begin{eqnarray*}y_1 &=& F(-1,-2,3;x)\\ &=& \sum_{n=0}^\infty\frac{(-1)_n(-2)_n}{(3)_n}\frac{x^n}{n!}\\ &=&1+\frac{2}{3}x\\ &=& \frac{1}{3}(2t-1)\end{eqnarray*}2つ目は階数低減法でやります.$y_2=u(x)(2x+3)$ とおいてやります。答えは煩雑になります(wolframで計算可能)。
次の記事:
本記事では、下記の本を大いに参考にしています。厳密性はほどほどに、なるべくたくさんの演習問題が用意されています。産業や自然界における事例も豊富。数学科以外の理学部・工学部生にオススメです。

【Amazon】常微分方程式 (技術者のための高等数学)
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。