ここまでの流れは過去記事参照:
フックス型微分方程式と確定特異点2 (RiemannのP方程式)
本記事ではこれらの内容をガンガン使います。
もくじ
詳しくは前回までの記事を見てください。2階の方程式に限ります。
$u''+p(z)u+q(z)u=0$ において $p(z)$ , $q(z)$ が有理型関数であり、その方程式の特異点がすべて確定特異点であるものをフックス型微分方程式(Fuchsian equation)という。
このうち、確定特異点がちょうど3つの場合は次の「リーマンのP方程式」となります。
リーマンのP微分方程式\begin{eqnarray}&&u''+\left(\frac{1-\a-\a'}{z-a}+\frac{1-\b-\b'}{z-b}+\frac{1-\g-\g'}{z-c}\right)u'\\&&\quad+\left(\frac{\a\a'(a-b)(a-c)}{z-a}+\frac{\b\b'(b-a)(b-c)}{z-b}+\frac{\g\g'(c-a)(c-b)}{z-c}\right)\\&&\quad\quad\quad\times\frac{u}{(z-a)(z-b)(z-c)}=0\tag{0.1}\end{eqnarray}(ただし $\a+\a'+\b+\b'+\g+\g'=1$)
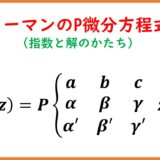
の6つの特殊解は$$(z-a)^{\a}\sum_{n=0}^\infty a_n(z-a)^{n}\quad,\quad (z-a)^{\a'}\sum_{n=0}^\infty a'_n(z-a)^{n}$$$$(z-b)^{\b}\sum_{n=0}^\infty b_n(z-b)^{n}\quad,\quad (z-b)^{\b'}\sum_{n=0}^\infty b'_n(z-b)^{n}$$$$(z-c)^{\g}\sum_{n=0}^\infty c_n(z-c)^{n}\quad,\quad (z-c)^{\g'}\sum_{n=0}^\infty c'_n(z-c)^{n}$$と表され、任意の解を$$u(z)=P\left\{\begin{matrix}a & b & c\\\a & \b & \g\\\a' & \b' & \g'\end{matrix}\;z\right\}$$と表され、任意の解を$$u(z)=P\left\{\begin{matrix}a & b & c\\\a & \b & \g\\\a' & \b' & \g'\end{matrix}\;z\right\}$$と表記する。
以上の事実は、いずれかの特異点を $\infty$ としても成り立つ。
参考文献はWhittaker & Watsonです。
古いですが有名な書物で、どんどん改訂版が出ています。前半は解析学一般、後半は特殊関数という内容で、網羅的に勉強できます。演習問題に解答がないのが昔ながらのものって感じ。2022/11/6現在、最新版は5th Editionで私も所有していますが、廉価な3rdとかでも十分かと。

A Course of Modern Analysis: fifth Edition

A Course of Modern Analysis: Third Edition
複素関数論で現れるメビウス変換(Möbius transformation)とは、\begin{equation}\zeta=\frac{Az+B}{Cz+D}\;,\quad AD-BC\neq0\tag{1.1}\end{equation}なる変数変換のことです。一次分数変換ともよばれます。$AD-BC=0$ ではただの定数になってしまうので除外しています。
メビウス変換で $C=0$ とすると $\zeta=z+a$ のように表すことができ、複素平面上の平行移動となります。また $A=0$ , $B=C=D=1$ で反転変換 $\zeta=1/z$ になります。これまでにも扱いましたね。このようにメビウス変換は、基本的な変換を包括しています。
またメビウス変換はフックス型方程式に応用することで、面白い特性をあらわにします。ここでは\begin{equation}\zeta=\frac{z+A}{z+B}\;,\;z+A\;,\;\frac{1}{z+B}\tag{1.2}\end{equation}という形のみ現れます。
特異点の移動と方程式の不変性
ウォーミングアップです。過去記事の例題3と同様の議論により、確定特異点が $a$ のみのフックス型方程式は\begin{equation}u''(z)+\frac{2}{z-a}u'(z)=0\tag{2.1}\end{equation}と表されます。実質、1階の方程式なので簡単に解けます。ここで $\zeta=z-a$ なるメビウス変換(平行移動)をすると $f(\zeta):=u(\zeta+a)$ として\begin{equation}f''(\zeta)+\frac{2}{\zeta}f'(\zeta)=0\tag{2.2}\end{equation}方程式の特異点が $a$ から $0$ に移ったことが分かります。それ以外は(2.1)と形が何ら変化していないことも分かります。
あるいは平行移動+反転である $\zeta=\frac{1}{z-a}$ としましょう。$u(\frac{1}{\zeta}+a)=f(\zeta)$ とすると$$\frac{du}{dz}=-\zeta^2\frac{df}{d\zeta}\;,\;\frac{d^2u}{dz^2}=\zeta^4\frac{d^2f}{d\zeta^2}+2\zeta^3\frac{df}{d\zeta}$$これらを用いると、(2.1)は何と\begin{equation}f''(\zeta)=0\tag{2.3}\end{equation}なる微分方程式に変換されます。以前に見たように、これは確定特異点を $\infty$ にのみもつフックス型微分方程式であり、(2.1)で $a\to\infty$ としたものです。
このようにメビウス変換を2種類やってみたところ、いずれも微分方程式(2.1)の形はそのままに、特異点のみが移動しました。
解への応用
(2.3)の解は$$f(\zeta)=A\zeta+B$$です。したがって $u(z)=f(\zeta)$ , $\zeta=\frac{1}{z-a}$ より$$u(z)=\frac{A}{z-a}+B$$と(2.1)の解が得られます。試しに変数分離などで(2.1)を普通に解いてみると、同じ一般解が得られます。この例ではそれほどありがたみはありませんが、(2.3)が解けるとただちに(2.1)が解けることになるわけです。なのでここでの結論として
確定特異点を1つもつフックス型微分方程式は、本質的に$$u''=0$$のみである。
と述べておきます。要は、これさえ解ければ他のもぜんぶ解けるよという意味です。
2点を一気に移す変換
確定特異点を移すことで方程式は簡単にも難解にもなります。先ほどの話からも推測できるように、確定特異点は一般の $a$ などよりも $0$ や $\infty$ であったほうが式をシンプルにできます。
いま2点 $a,b$ があるとします。$a$ を $\infty$ へ、$b$ を $0$ へ移すメビウス変換は\begin{equation}\zeta=\frac{z-b}{z-a}\tag{3.1}\end{equation}です。これはまた $\zeta=1+\frac{a-b}{z-a}$ や $z=\frac{a\zeta-b}{\zeta-1}$ とも書けます。
$u(z)$ は $u\left(\frac{a\zeta-b}{\zeta-1}\right):=f(\zeta)$ に移りますので\begin{equation}u'(z)=-\frac{(\zeta-1)^2}{a-b}f'(\zeta)\tag{3.2}\end{equation}\begin{equation}u''(z)=\frac{(\zeta-1)^3}{(a-b)^2}\left[(\zeta-1)f''(\zeta)+2f'(\zeta)\right]\tag{3.3}\end{equation}のように変換されます。
方程式の変換と不変性
確定特異点が $a,b$ であるときのフックス型方程式は、確定特異点が $a,b,c$ であるときのフックス型方程式(すなわちリーマンP方程式(0.1))で $c\to a$ とすることで作れます。すなわち\begin{equation}u''+\left(\frac{1+\b+\b'}{z-a}+\frac{1-\b-\b'}{z-b}\right)u'+\frac{\b\b'(a-b)}{(z-a)(z-b)}\left(\frac{1}{z-a}-\frac{1}{z-b}\right)u=0\tag{3.4}\end{equation}これは過去記事の命題1Cとも一致しており、間違いありません。 ※なので(0.1)は特異点2つの場合を含んでいる!
この方程式に対して(3.1)のメビウス変換を行うと(3.2)(3.3)を用いて\begin{equation}\frac{d^2f}{d\zeta^2}+\frac{1-\b-\b'}{\zeta}\frac{df}{d\zeta}+\frac{\b\b'}{\zeta^2}f=0\tag{3.5}\end{equation}これは過去記事の例題4で個別に求めたものと一致しており、確かに確定特異点が $\zeta=0,\infty$ に移っています。また(3.4)で $a=\infty$ , $b=0$ としたものと同じですので、特異点が移ったことを除いて方程式は不変であることが分かります。
確定特異点を2つもつフックス型微分方程式は、本質的に(3.5)のみである。
完全な解を求める
ここまでの話を使えば(3.4)すなわち「確定特異点を2つもつフックス型方程式」を完全に解くことができます。しかも解はすべて初等関数なのです。
(3.5)はオイラー・コーシー方程式の形をしています。試行解 $\zeta^r$ を代入すると$$r(r-1)+(1-\b-\b')r+\b\b'=0$$を得ます。よって $r=\b,\b'$ です。したがって $\b\neq\b'$ であれば独立な特殊解 $\zeta^\b$ , $\zeta^{\b'}$ が得られます。 $\zeta$ を $z$ へ戻すと一般解は任意定数 $A,B$ を用いて\begin{equation}u(z)=A\left(\frac{z-b}{z-a}\right)^\beta+B\left(\frac{z-b}{z-a}\right)^{\beta'}\tag{3.6}\end{equation}となります。
$\b=\b'$ のときは特殊解 $\zeta^\b$ に対して $\zeta^\b v(\zeta)$ なる試行解を方程式に代入すると$$\zeta v''(\zeta)+v'(\zeta)=0$$であり、変数分離などの基本的操作で $v(\zeta)=C\ln\zeta+C'$ となります。よって一般解は\begin{equation}u(z)=A\left(\frac{z-b}{z-a}\right)^\beta+B\left(\frac{z-b}{z-a}\right)^{\beta}\ln\frac{z-b}{z-a}\tag{3.7}\end{equation}
まとめると
(3.4)で表される方程式の解は$$u(z)=A\left(\frac{z-b}{z-a}\right)^\beta+B\left(\frac{z-b}{z-a}\right)^{\beta'}\quad(\b\neq\b')$$$$u(z)=A\left(\frac{z-b}{z-a}\right)^\beta+B\left(\frac{z-b}{z-a}\right)^{\beta}\ln\frac{z-b}{z-a}\quad(\b=\b')$$
具体例を解いてみよう
\begin{equation}u''+\frac{2z}{z^2-1}u'-\frac{u}{(z^2-1)^2}=0\tag{4.1}\end{equation}がフックス型であることを示し、確定特異点をすべて挙げよ。そのうえで(4.1)を(3.4)の形で表し、メビウス変換によって一般解を求めよ。
【解答】$z=\infty$ で $zp(z)=2$ かつ $z^4q(z)$ が正則なので、確定特異点は $\pm 1$ の2点のみであり、他に特異点をもたないためフックス型といえる。$\zeta=\frac{z+1}{z-1}$ なる変換により $u(z)=f(\zeta)$ として$$\zeta^2f''(\zeta)+\zeta f'(\zeta)-\frac{1}{4}f(\zeta)=0$$である。これはオイラー・コーシー型であり、解は$$f(\zeta)=A\sqrt{\zeta}+\frac{B}{\sqrt{\zeta}}$$したがって一般解は$$u(z)=A\sqrt{\frac{z+1}{z-1}}+B\sqrt{\frac{z-1}{z+1}}$$あるいは次のようにも書ける。$$u(z)=\frac{Cz+D}{\sqrt{1-z^2}}$$【解答終】
次回は3つの確定特異点を移す話をしましょう。
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。