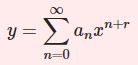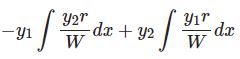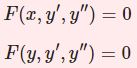2階の非斉次方程式では、斉次方程式の一般解にもう１つの特殊解を加えることで解を得る。よって「もう１つの特殊解」を見つけることがポイントとなる。今回はその方法として「定数変化法」を紹介する。
非斉次2階線型微分方程式$$y^{\prime\prime}+p(x)y'+q(x)y=r(x)$$の特殊解を定数変化法によって求める．
非斉次方程式は斉次方程式 $r(x)=0$ であった場合の一般解を求め、それにもう１つの特殊解を足し合わせることで解くことができます。
$$y^{\prime\prime}+p(x)y'+q(x)y=0$$の一般解 $y_0$ を導出。任意定数を２つ含む。
※過去記事で解説済
$$y^{\prime\prime}+p(x)y'+q(x)y=r(x)$$の特殊解 $y_p$ を見つける。
・試行解による方法（過去記事）
・定数変化法（本記事の要点）
$y=y_0+y_p$ が最終的な答えである。
斉次一般解の求め方は
【D5】斉次2階線型微分方程式
【D7】オイラー・コーシーの方程式
を参照ください。
非斉次の特殊解の見つけ方の１つである「試行解による方法」はこちら
【D8】非斉次2階線型微分方程式その１
試行解による方法は分かりやすいのですが、職人技であり、うまく思いついた時しか機能しません。今回はより一般的に解ける「定数変化法」を解説します。
斉次方程式 $y^{\prime\prime}+p(x)y'+q(x)y=0$ の線型独立な２解 $y_1,y_2$ を得たとします。このとき非斉次方程式 $y^{\prime\prime}+p(x)y'+q(x)y=r(x)$ の特殊解は
$$y_p=-y_1\int\frac{y_2r}{W}dx+y_2\int\frac{y_1r}{W}dx$$ただし $W$ はロンスキアンで$$W\equiv\left| \begin{matrix}y_1 & y_2\\y'_1 & y'_2\end{matrix}\right|=y_1y'_2-y_2y'_1$$
です。
実際に $y_p$ が解になっているか確認しましょう。まず\begin{eqnarray*}y'_p&=& -y'_1 \int\frac{y_2r}{W}dx -y_1\frac{y_2r}{W}+y'_2\int\frac{y_1r}{W}dx+y_2\frac{y_1r}{W}\\ &=& -y'_1 \int\frac{y_2r}{W}dx +y'_2\int\frac{y_1r}{W}dx\end{eqnarray*}2階微分は\begin{eqnarray*}y^{\prime\prime}_p&=& -y^{\prime\prime}_1 \int\frac{y_2r}{W}dx-y'_1\frac{y_2r}{W}+y^{\prime\prime}_2\int\frac{y_1r}{W}dx+y'_2\frac{y_1r}{W}\\ &=& -y^{\prime\prime}_1 \int\frac{y_2r}{W}dx+y^{\prime\prime}_2\int\frac{y_1r}{W}dx+r\end{eqnarray*} これらを微分方程式の左辺に代入すると\begin{eqnarray*} y_p^{\prime\prime}+p(x)y_p'+q(x)y_p &=& -y^{\prime\prime}_1 \int\frac{y_2r}{W}dx+y^{\prime\prime}_2\int\frac{y_1r}{W}dx+r -p\left(y'_1 \int\frac{y_2r}{W}dx -y'_2\int\frac{y_1r}{W}dx\right)+q\left(-y_1\int\frac{y_2r}{W}dx+y_2\int\frac{y_1r}{W}dx\right)\\ &=& r-(y_1^{\prime\prime}+py'_1+qy_1)\int\frac{y_2r}{W}dx+(y_2^{\prime\prime}+py'_2+qy_2)\int\frac{y_1r}{W}dx \\&=& r\end{eqnarray*} と右辺に一致しているので確かに $y_p$ は解ですね。
ということでこの公式を使って例題を解いてみましょう。
$y^{\prime\prime}+y=\sec x$ を解け．
斉次方程式 $y^{\prime\prime}+y=0$ の独立な2解は $y_1=\sin x$ , $y_2=\cos x$ なので斉次一般解は$$y_0=a\sin x +b\cos x$$です。
ロンスキアンは$$W=-\sin^2 x-\cos^2 x=-1$$ なので特殊解は\begin{eqnarray*}y_p&=&-\sin x\int(-\cos x\sec x)dx+\cos x\int(-\sin x\sec x)dx\\&=& \sin x\int 1dx-\cos x\int\tan xdx\\&=& \sin x\cdot (x+c_1)+\cos x(\log|\cos x|+c_2)\end{eqnarray*}$y_0$ を含んでいますのでこれがそのまま求める一般解です。$$\therefore\quad y=(x+c_1)\sin x+(\log|\cos x|+c_2)\cos x$$
$y^{\prime\prime}-4y'+4y=\displaystyle\frac{e^{2x}}{x}$ を解け．
斉次の2解は $y_1=xe^{2x}$ , $y_2=e^{2x}$ です。定数係数の方程式で重解が出てしまうケースですね（過去記事）。
ロンスキアンは$$W=\left| \begin{matrix}xe^{2x} & e^{2x}\\(2x+1)e^{2x} & 2e^{2x}\end{matrix}\right|=-e^{4x}$$特殊解を計算すると\begin{eqnarray*}y_p&=& -xe^{2x}\int\frac{e^{2x}\frac{e^{2x}}{x}}{-e^{4x}}dx+e^{2x}\int\frac{xe^{2x}\frac{e^{2x}}{x}}{-e^{4x}}dx\\&=& xe^{2x}\int\frac{dx}{x}-e^{2x}\int dx\\&=& xe^{2x}(\log x+c_1)-e^{2x}(x+c_2)\end{eqnarray*}斉次一般解を含んでいるのでこれがそのまま答えとなります。あるいは定数を別のとりかたにすると$$y=axe^{2x}+c_2e^{2x}+xe^{2x}\log x$$とも書けます。こっちのほうが見やすいかな？
$x^2y^{\prime\prime}-4xy'+6y=21x^{-4}$ を解け．
斉次方程式 $x^2y^{\prime\prime}-4xy'+6y=0$ はオイラー・コーシーの方程式です（過去記事）。試行解 $x^n$ を代入して $n$ の値を決定してください。すると $y_1=x^3$ , $y_2=x^2$ を得ます。よって斉次一般解は$$y_0=c_1x^3+c_2x^2$$
ロンスキアンは$$W=\left| \begin{matrix}x^3 & x^2\\3x^2 & 2x\end{matrix}\right|=-x^4$$与えられた方程式を $x^2$ で割ると$$y^{\prime\prime}-\frac{4}{x}y'+\frac{6}{x^2}y=21x^{-6}$$すなわち$r(x)=21x^{-6}$ です。これを用いて\begin{eqnarray*}y_p&=& -x^3\int\frac{21x^{-4}}{-x^4}dx+x^2\int\frac{21x^{-3}}{-x^4}dx\\&=& -3x^{-4}+\frac{7}{2}x^{-4}\\&=& \frac{1}{2x^4}\end{eqnarray*}これまでで見たように、積分定数をつけて現れる項はどうせ斉次一般解なので、今回は定数をつけずにやりました。よって求める一般解は$$y=y_0+y_p=c_1x^3+c_2x^2+\frac{1}{2x^4}$$
質量 $m$ の物体がばね定数 $m\omega^2_0$ のばねに取り付けられている．時刻 $t=0$ においてこの物体の変位 $x(0)=0$ , 速度 $\dot{x}(0)=0$ であったところに $F(t)=mA\sin 2\omega_0t$ なる力を加えるとき，この物体の運動方程式を解け．
運動方程式は$$m\ddot{x}=-m\omega^2_0 x+mA\sin 2\omega_0t$$$$\therefore\quad \ddot{x}+\omega^2_0x=A\sin2\omega_0t$$斉次方程式 $ \ddot{x}+\omega^2_0x= 0$ の独立な2解は $\sin \omega_0t$ , $\cos\omega_0 t$ です。ロンスキアンは $W=-\omega_0$ と求まるので非斉次特殊解は$$x_p(t)=-\frac{A}{3\omega^2_0}\sin 2\omega_0t$$よって一般解は$$x(t)=a\sin\omega_0t+b\cos\omega_0t -\frac{A}{3\omega^2_0}\sin 2\omega_0t $$初期条件から定数 $a$ と $b$ は定まって$$x(t)=\frac{2A}{3\omega^2_0}\sin\omega_0t(1-\cos\omega_0t)$$と解けます。
以上、2回にわたって非斉次2階微分方程式の解法を紹介しました！次はこちら：
【D10】高階線型微分方程式の指針と例題
本記事では、下記の本を大いに参考にしています。厳密性はほどほどに、なるべくたくさんの演習問題が用意されています。産業や自然界における事例も豊富。数学科以外の理学部・工学部生にオススメです。
【Amazon】常微分方程式 (技術者のための高等数学)
常微分シリーズ過去記事
Please support me!
記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。