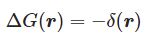【物理数学】N次元グリーン関数の解法(2)

前回から上記のテーマで書いています。前回は $N=1～3$ の場合の $G$ を求めました。本記事も同様の流れになりますので、読む前に参考にしてください。

2021年12月8日 【物理数学】N次元グリーン関数の解法(1)

今回は4次元でも同様に解を求め、最後に $N$ 次元での解を考えます。フーリエ変換、デルタ関数、ベッセル関数とそれに関する積分公式など、数学トピックが詰まっているのでいい勉強になると思います。

4次元の場合

4次元の場合、座標を $\boldsymbol{x}=(x_1,x_2,x_3,x_4)$ と表せばグリーン関数 $G(\boldsymbol{x})$ が満たす微分方程式は\begin{equation}\Delta G(\boldsymbol{x})=-\delta^4 (\boldsymbol{x})\tag{1}\end{equation}となります。

$\boldsymbol{k}=(k_1,k_2,k_3,k_4)$ , $k^2=k_1^2+k_2^2+k_3^2+k_4^2$ として $G$ をフーリエ変換すれば\begin{equation}\tilde{G}(\boldsymbol{k})=\int G(\boldsymbol{x})e^{-i\boldsymbol{k}\cdot\boldsymbol{x}}d^4x\end{equation}ここで $d^4x=dx_1dx_2dx_3dx_4$ としています。さらに逆フーリエ変換すれば\begin{equation}G(\boldsymbol{x})=\frac{1}{16\pi^4}\int\tilde{G}(\boldsymbol{k})e^{i\boldsymbol{k}\cdot\boldsymbol{x}}d^4k\end{equation}となります。これに4次元ラプラシアンを作用させて\begin{eqnarray}\Delta G(\boldsymbol{x}) &=& \frac{1}{16\pi^4}\int\tilde{G}(\boldsymbol{k})\Delta e^{i\boldsymbol{k}\cdot\boldsymbol{x}}d^4k\\ &=&-\frac{1}{16\pi^4}\int\tilde{G}(\boldsymbol{k})k^2 e^{i\boldsymbol{k}\cdot\boldsymbol{x}}d^4k\end{eqnarray}このラプラシアンは $\boldsymbol{x}$ に関する微分作用素なので $\boldsymbol{k}$ にはかかりません。

一方、デルタ関数のフーリエ変換は\begin{equation}\delta^4(\boldsymbol{x})=\frac{1}{16\pi^4}\int e^{i\boldsymbol{k}\cdot\boldsymbol{x}}d^4k\end{equation}以上より(1)は以下のように書き換えられます。\begin{equation}-\frac{1}{16\pi^4}\int\tilde{G}(\boldsymbol{k})k^2 e^{i\boldsymbol{k}\cdot\boldsymbol{x}}d^4k=-\frac{1}{16\pi^4}\int e^{i\boldsymbol{k}\cdot\boldsymbol{x}}d^4k\end{equation}両辺を比べて\begin{equation}\tilde{G}(\boldsymbol{k})=\frac{1}{k^2}\end{equation}となります。この逆変換が求める解であり、\begin{equation}G(\boldsymbol{x})=\frac{1}{16\pi^4}\int\frac{1}{k^2}e^{i\boldsymbol{k}\cdot\boldsymbol{x}}d^4k\end{equation}となります。ここまでは2次元、3次元のときと全く同じです。

全空間にわたる積分ですので極座標に置換すると\begin{eqnarray*}G(\boldsymbol{x})&=&\frac{1}{16\pi^4}\int\frac{1}{k^2}e^{i\boldsymbol{k}\cdot\boldsymbol{x}}d^4k\\&=&\frac{1}{16\pi^4}\int^\infty_0dk\int^{2\pi}_0d\theta_1\int^{\pi}_0d\theta_2\int^{\pi}_0d\theta_3\frac{1}{k^2}e^{ikx\cos\theta_3}k^3\sin^2\theta_3\sin\theta_2\\&=&\frac{1}{4\pi^3}\int^\infty_0dk\;k\int^{\pi}_0e^{ikx\cos\theta_3}\sin^2\theta_3d\theta_3\\&=& \frac{1}{4\pi^3}\int^\infty_0dk\;k\int^{\pi}_0e^{ikx\cos\theta}\sin^2\theta d\theta\\&=& \frac{1}{8\pi^3}\int^\infty_0dk\;k\int^{\pi}_0e^{ikx\cos\theta}(1-\cos2\theta)d\theta \end{eqnarray*}Hansen-Besselの公式によると第1種ベッセル関数 $J_n(z)$ は以下のように積分表示されます。\begin{equation}J_n(z)=\frac{1}{\pi i^n}\int^\pi_0e^{iz\cos\theta}\cos n\theta d\theta\end{equation}この公式の導出については

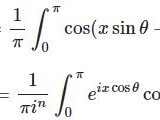2021年12月11日 第1種ベッセル関数の積分表示とその導出

を参照してください。
よって\begin{eqnarray*}G(\boldsymbol{x})&=&\frac{1}{8\pi^3}\int^\infty_0dk\;k\int^{\pi}_0e^{ikx\cos\theta}(1-\cos\theta)d\theta\\&=&\frac{1}{8\pi^2}\int^\infty_0dk\;k[J_0(kx)+J_2(kx)]\end{eqnarray*}第1種ベッセル関数における漸化式

$$J_{\nu+1}(z)+J_{\nu-1}(z)=\frac{2\nu}{z}J_\nu(z)$$を用いると（ベッセル関数については関連記事をご覧ください）、 \begin{eqnarray*} G(\boldsymbol{x}) &=& \frac{1}{8\pi^2}\int^\infty_0dk\;k \frac{2}{kx}J_1(kx)\\&=& \frac{1}{4\pi^2x}\int^\infty_0J_1(kx)dk\end{eqnarray*} さらに第1種ベッセル関数の微分を含んだ漸化式$$\frac{d}{dz}(t^{-\nu} J_\nu(z))=-z^{-\nu} J_{\nu+1}(z)$$
より $\frac{d}{dz}(J_0(z))=-J_1(z)$ を得ますので$$ G(\boldsymbol{x}) = \frac{1}{4\pi^2x^2}\Bigl[-J_0(kx)\Bigr] ^\infty_{k=0}$$$J_0(0)=1$ , $\displaystyle\lim_{t\to\infty}J_0(t)=0$ なので結局$$\therefore\;G(\boldsymbol{x})=\frac{1}{4\pi^2|\boldsymbol{x}|^2}$$

５次元の場合

先ほどと同様に進めれば\begin{equation}G(\boldsymbol{x})=\frac{1}{32\pi^5}\int\frac{1}{k^2}e^{i\boldsymbol{k}\cdot\boldsymbol{x}}d^5k\end{equation}極座標に置換すると
$$\begin{cases}k_1&=&k\sin\theta_4\sin\theta_3\sin\theta_2\cos\theta_1\\k_2&=&k\sin\theta_4\sin\theta_3\sin\theta_2\sin\theta_1\\k_3&=&k\sin\theta_4\sin\theta_3\cos\theta_2\\k_4&=&k\sin\theta_4\cos\theta_3\\k_5&=&k\cos\theta_4\end{cases}$$となり、$$d^5k=k^4\sin^3\theta_4\sin^2\theta_3\sin\theta_2dkd\theta_1d\theta_2d\theta_3 d\theta_4$$
を得ますから、全空間にわたる積分は\begin{eqnarray*}G(\boldsymbol{x})&=&\frac{1}{32\pi^5}\int\frac{1}{k^2}e^{i\boldsymbol{k}\cdot\boldsymbol{x}}d^5k\\&=&\frac{1}{32\pi^5}\int^\infty_0\hskip -1em dk\int^{2\pi}_0\hskip -1em d\theta_1\int^{\pi}_0\hskip -1em d\theta_2\int^{\pi}_0\hskip -1em d\theta_3\int^{\pi}_0\hskip -1em d\theta_4\frac{1}{k^2}e^{ikx\cos\theta_4}k^4\sin^3\theta_4\sin^2\theta_3\sin\theta_2\\&=&\frac{1}{16\pi^3}\int^\infty_0dk\;k^2\int^{\pi}_0e^{ikx\cos\theta}\sin^3\theta d\theta\\&=&\frac{1}{16\pi^3}\int^\infty_0dk\;k^2\int^{\pi}_0[\cos(kx\cos\theta)+i\sin(kx\sin\theta)]\sin^3\theta d\theta \end{eqnarray*}ここで第2項の積分は虚部となっていますが区間を半分で分けて片方を $\phi=\pi-\theta$ と置換して計算します。\begin{eqnarray*}\int^{\pi}_0\sin(kx\cos\theta)\sin^3\theta d\theta&=&\int^{\frac{\pi}{2}}_0\sin(kx\cos\theta)\sin^3\theta d\theta+\int^{\pi}_{\frac{\pi}{2}}\sin(kx\cos\theta)\sin^3\theta d\theta\\&=&\int^{\frac{\pi}{2}}_0\sin(kx\cos\theta)\sin^3\theta d\theta+\int^{0}_{\frac{\pi}{2}}\sin(-kx\cos\phi)\sin^3\phi (-d\phi)\\&=&\int^{\frac{\pi}{2}}_0\sin(kx\cos\theta)\sin^3\theta d\theta+\int^{0}_{\frac{\pi}{2}}\sin(kx\cos\theta)\sin^3\theta d\theta \\&=& 0\end{eqnarray*}よって虚部は省いて$$ G(\boldsymbol{x}) = \frac{1}{16\pi^3}\int^\infty_0dk\;k^2\int^{\pi}_0\cos(kx\cos\theta)\sin^3\theta d\theta $$$\sin^3$ があるので、2次元,4次元のときに使ったHansen-Besselの公式がそのままでは使えません。困ってしまったので『岩波数学公式』に頼ることにします。本書によれば、Lommelの積分表示\begin{equation}\int^{\pi}_0\cos(z\cos\theta)\sin^{2\nu}\theta d\theta=\frac{\sqrt{\pi}\Gamma(\nu+\frac{1}{2})}{(z/2)^\nu}J_\nu(z)\end{equation}なるものがあるようです。$\nu=3/2$ とすれば\begin{eqnarray*}G(\boldsymbol{x})&=&\frac{1}{16\pi^3}\int^\infty_0dk\; k^2\int^{\pi}_0\cos(kx\cos\theta)\sin^3\theta d\theta\\&=& \frac{1}{16\pi^3}\int^\infty_0dk\; k^2\frac{2\sqrt{2\pi}}{(kx)^\frac{3}{2}}J_\frac{3}{2}(kx)\\&=& \frac{\sqrt{2\pi}}{8\pi^3x^2}\int^\infty_0\sqrt{kx}J_\frac{3}{2}(kx)dk\\&=&  \frac{\sqrt{2\pi}}{8\pi^3x^2}\int^\infty_0\sqrt{\frac{2}{\pi}}\left(\frac{\sin kx}{kx}-\cos kx\right)dk \\&=&\frac{1}{4\pi^3x^2}\int^\infty_0\left(\frac{\sin kx}{kx}-\cos kx\right)dk\end{eqnarray*}となります。被積分関数の第1項は $\frac{\pi}{2x}$ です。第2項が通常の意味では発散しますが$\cos kx$ の波数 $k$ をあらゆる正の実数として重ね合わせると $x\neq0$ で $0$ となることから、積分値を$0$とすると$$ G(\boldsymbol{x}) = \frac{1}{8\pi^2|\boldsymbol{x}|^3} $$と求まります。

途中で現れたLommelの積分表示の証明は以下の記事で書いています。

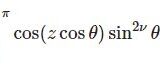2021年12月12日 第1種ベッセル関数の積分表示(2) ポアソンの公式の導出

$N$ 次元の場合

いよいよ $N$ 次元でやってみます。これまで１～５次元とやってきましたが、ここまでくると一般の $N$ でもやれそうな気がします。ただし以下の解法は $N\ge3$ という条件付きで通用することに注意。方針は、まずフーリエ変換してグリーン関数を積分表示し、極座標へ置換して全空間積分をします。すると第1種ベッセル関数が登場するのでそれを計算できればOKです。

$G$ をフーリエ変換すれば $\boldsymbol{k}=(k_1,k_2,\cdots,k_N)$ , $k^2=k_1^2+k_2^2+\cdots+k_N^2$ として\begin{equation}\tilde{G}(\boldsymbol{k})=\int G(\boldsymbol{x})e^{-i\boldsymbol{k}\cdot\boldsymbol{x}}d^Nx\end{equation}ここで $d^Nx=dx_1dx_2\cdots dx_N$ としています。さらに逆フーリエ変換すれば\begin{equation}G(\boldsymbol{x})=\frac{1}{(2\pi)^N}\int\tilde{G}(\boldsymbol{k})e^{i\boldsymbol{k}\cdot\boldsymbol{x}}d^Nk\end{equation}となります。これに $N$ 次元ラプラシアンを作用させて\begin{eqnarray*}\Delta G(\boldsymbol{x}) &=& \frac{1}{(2\pi)^N}\int\tilde{G}(\boldsymbol{k})\Delta e^{i\boldsymbol{k}\cdot\boldsymbol{x}}d^Nk\\ &=&-\frac{1}{(2\pi)^N}\int\tilde{G}(\boldsymbol{k})k^2 e^{i\boldsymbol{k}\cdot\boldsymbol{x}}d^Nk\end{eqnarray*}このラプラシアンは $\boldsymbol{x}$ に関する微分作用素なので $\boldsymbol{k}$ にはかかりません。

一方、デルタ関数は\begin{equation}\delta^N(\boldsymbol{x})=\frac{1}{(2\pi)^N}\int e^{i\boldsymbol{k}\cdot\boldsymbol{x}}d^Nk\end{equation}ですので方程式は以下のように書き換えられます。\begin{equation}-\frac{1}{(2\pi)^N}\int\tilde{G}(\boldsymbol{k})k^2 e^{i\boldsymbol{k}\cdot\boldsymbol{x}}d^Nk=-\frac{1}{(2\pi)^N}\int e^{i\boldsymbol{k}\cdot\boldsymbol{x}}d^Nk\end{equation}両辺を比べて\begin{equation}\tilde{G}(\boldsymbol{k})=\frac{1}{k^2}\end{equation}となります。この逆変換が求める解であり、\begin{equation}G(\boldsymbol{x})=\frac{1}{(2\pi)^N}\int\frac{1}{k^2}e^{i\boldsymbol{k}\cdot\boldsymbol{x}}d^Nk\end{equation}となります。

極座標に置換すると$$\begin{cases}k_1&=&k\sin\theta_{N-1}\sin\theta_{N-2}\cdots\sin\theta_2\cos\theta_1\\k_2&=&k\sin\theta_{N-1}\sin\theta_{N-2}\cdots\sin\theta_2\sin\theta_1\\k_3&=&k\sin\theta_{N-1}\sin\theta_{N-2}\cdots\cos\theta_2\\&\vdots&\\k_N&=&k\cos\theta_{N-1}\end{cases}$$となり、$$d^Nk=k^{N-1}\sin^{N-2}\theta_{N-1}\sin^{N-3}\theta_{N-2}\cdots\sin\theta_2dkd\theta_1d\theta_2\cdots d\theta_{N-1}$$を得ますから、全空間にわたる積分は\begin{eqnarray*}G(\boldsymbol{x})&=&\frac{1}{(2\pi)^N}\int\frac{1}{k^2}e^{i\boldsymbol{k}\cdot\boldsymbol{x}}d^Nk\\&=&\frac{1}{(2\pi)^N}\int^\infty_0\hskip -1em dk\int^{2\pi}_0\hskip -1em d\theta_1\int^{\pi}_0\hskip -1em d\theta_2\cdots\int^{\pi}_0\hskip -1em d\theta_{N-1}\frac{1}{k^2}e^{ikx\cos\theta_{N-1}}k^{N-1}\sin^{N-2}\theta_{N-1}\sin^{N-3}\theta_{N-2}\cdots\sin\theta_2\\&=&\frac{1}{(2\pi)^{N-1}}\left(\int^{\pi}_0\hskip -1em \sin\theta d\theta\right) \left(\int^{\pi}_0\hskip -1em \sin^2\theta d\theta\right)\cdots\left(\int^{\pi}_0\hskip -1em \sin^{N-3}\theta d\theta\right)\int^\infty_0\hskip -1em dk\;k^{N-3}\int^{\pi}_0e^{ikx\cos\theta}\sin^{N-2}\theta d\theta\\&=&\frac{1}{(2\pi)^{N-1}}\prod^{N-3}_{n=1}\left(\int^{\pi}_0\hskip -1em \sin^n\theta d\theta\right)\int^\infty_0\hskip -1em dk\;k^{N-3}\int^{\pi}_0e^{ikx\cos\theta}\sin^{N-2}\theta d\theta\\&=&\frac{1}{(2\pi)^{N-1}}\prod^{N-3}_{n=1}\left(\sqrt{\pi}\frac{\Gamma(\frac{n+1}{2})}{\Gamma(\frac{n+2}{2})}\right)\int^\infty_0\hskip -1em dk\;k^{N-3}\int^{\pi}_0e^{ikx\cos\theta}\sin^{N-2}\theta d\theta\\&=&\frac{\pi^{\frac{N-3}{2}}}{(2\pi)^{N-1}}\frac{1}{\Gamma(\frac{N-1}{2})}\int^\infty_0\hskip -1em dk\;k^{N-3}\int^{\pi}_0e^{ikx\cos\theta}\sin^{N-2}\theta d\theta\\&=&\frac{\pi^{\frac{N-3}{2}}}{(2\pi)^{N-1}}\frac{1}{\Gamma(\frac{N-1}{2})}\int^\infty_0\hskip -1em dk\;k^{N-3}\int^{\pi}_0\{\cos(kx\cos\theta)+i\sin(kx\cos\theta)\}\sin^{N-2}\theta d\theta\end{eqnarray*}第2項は虚部となっていますが区間を半分で分けて片方を $\phi=\pi-\theta$ と置換して計算します。\begin{eqnarray*}&&\int^{\pi}_0\sin(kx\cos\theta)\sin^{N-2}\theta d\theta\\&=&\int^{\frac{\pi}{2}}_0\sin(kx\cos\theta)\sin^{N-2}\theta d\theta+\int^{\pi}_{\frac{\pi}{2}}\sin(kx\cos\theta)\sin^{N-2}\theta d\theta\\&=&\int^{\frac{\pi}{2}}_0\sin(kx\cos\theta)\sin^{N-2}\theta d\theta+\int^{0}_{\frac{\pi}{2}}\sin(-kx\cos\phi)\sin^{N-2}\phi (-d\phi)\\&=&\int^{\frac{\pi}{2}}_0\sin(kx\cos\theta)\sin^{N-2}\theta d\theta+\int^{0}_{\frac{\pi}{2}}\sin(kx\cos\theta)\sin^{N-2}\theta d\theta \\&=& 0\end{eqnarray*}よって虚部はゼロなのでもとの計算に立ち返ると\begin{equation}G(\boldsymbol{x})=\frac{\pi^{\frac{N-3}{2}}}{(2\pi)^{N-1}}\frac{1}{\Gamma(\frac{N-1}{2})}\int^\infty_0\hskip -1em dk\;k^{N-3}\int^{\pi}_0\cos(kx\cos\theta)\sin^{N-2}\theta d\theta\end{equation}ところで第1種ベッセル関数におけるLommelの積分表示は\begin{equation}\int^{\pi}_0\cos(z\cos\theta)\sin^{2\nu}\theta d\theta =\frac{\sqrt{\pi}\Gamma(\nu+\frac{1}{2})}{(\frac{z}{2})^\nu}J_\nu(z)\end{equation}と書かれます。この公式において $z=kx$ , $\nu=\frac{N}{2}-1$ と適用すれば\begin{eqnarray*}G(\boldsymbol{x})&=&\frac{\pi^{\frac{N-3}{2}}}{(2\pi)^{N-1}}\frac{1}{\Gamma(\frac{N-1}{2})}\int^\infty_0\hskip -1em dk\;k^{N-3}\int^{\pi}_0\cos(kx\cos\theta)\sin^{N-2}\theta d\theta\\&=&\frac{\pi^{\frac{N-3}{2}}}{(2\pi)^{N-1}}\frac{1}{\Gamma(\frac{N-1}{2})}\int^\infty_0\hskip -1em dk\;k^{N-3}\frac{\sqrt{\pi}\Gamma(\frac{N-1}{2})}{(\frac{kx}{2})^{\frac{N}{2}-1}}J_{\frac{N}{2}-1}(kx)\\&=&\frac{1}{(2\pi)^{\frac{N}{2}}x^{\frac{N}{2}-1}}\int^\infty_0 k^{\frac{N}{2}-2}J_{\frac{N}{2}-1}(kx)dk\end{eqnarray*}さらに以下で表されるWeberの積分\begin{equation}\int^\infty_0k^{\mu-1}J_\nu(kx)dk=\frac{2^{\mu-1}\Gamma(\frac{\nu+\mu}{2})}{x^\mu\Gamma(\frac{\nu-\mu}{2}+1)}\end{equation}において $\mu=\nu=\frac{N}{2}-1$ とすることで\begin{eqnarray*}G(\boldsymbol{x})&=&\frac{1}{(2\pi)^{\frac{N}{2}}x^{\frac{N}{2}-1}}\int^\infty_0 k^{\frac{N}{2}-2}J_{\frac{N}{2}-1}(kx)dk\\&=&\frac{1}{(2\pi)^{\frac{N}{2}}x^{\frac{N}{2}-1}}\frac{2^{\frac{N}{2}-2}\Gamma(\frac{N}{2}-1)}{x^{\frac{N}{2}-1}}\end{eqnarray*}

従って求めるグリーン関数は\begin{equation}\therefore\;G(\boldsymbol{x})=\frac{\Gamma(\frac{N}{2}-1)}{4\pi^{\frac{N}{2}}|\boldsymbol{x}|^{N-2}}\quad (N\ge 3)\end{equation}となりました！ここまでたどり着く過程でいろいろと勉強になってよかったと思います。なおこの解は $N\ge 3$ が前提ですので、$N=1,2$ については前記事で導出した$$G(x)=\frac{1}{2}|x|+b$$$$G(\boldsymbol{x})=- \frac{1}{2\pi}\log |\boldsymbol{x}| $$が解となります。

応援のおねがい

Please support me!

まめしば

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。

ご支援いただいた方は、こちらで確認できます。

◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。

◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。

OFUSEで応援を送る

◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。