\begin{multline}\sum_{k=m}^nf(k)=\frac{f(m)+f(n)}{2}+\int_m^nf(z)dz\\+i\int_0^\infty\frac{f(m+iy)-f(m-iy)-f(n+iy)+f(n-iy)}{e^{2\pi y}-1}dy\end{multline}
この公式を導出します。といってもこれ自体に興味を持ったのではありません。ガンマ関数の勉強をしていたときに必要になったので頑張って導出しました。計算がややこしかったですが。
公式名のもととなった人物 Niels Henrik Abel は普通「アーベル」とよばれるので、「アーベル・プラナの和公式」とするのが適切との指摘をいただきました。最近wikipediaでもこちらに変更されています。
周回積分の定義
2つの整数を $m\le n$ とします。複素数 $z=x+iy$ の関数 $f(z)$ は $m\le \mathfrak{R}z\le n$ で解析的かつ有界とします。
いま積分\begin{equation}\oint_Cf(z)\pi\cot\pi zdz\tag{1}\end{equation}を考えます。経路 $C$ は下図の全体を1周するものです。向きに注意して表すと$$C=\G_{15}+\G_{11}+\G_{12}+\G_{13}+\G_{14}-\G_{24}-\G_{23}-\G_{22}-\G_{21}-\G_{25}$$
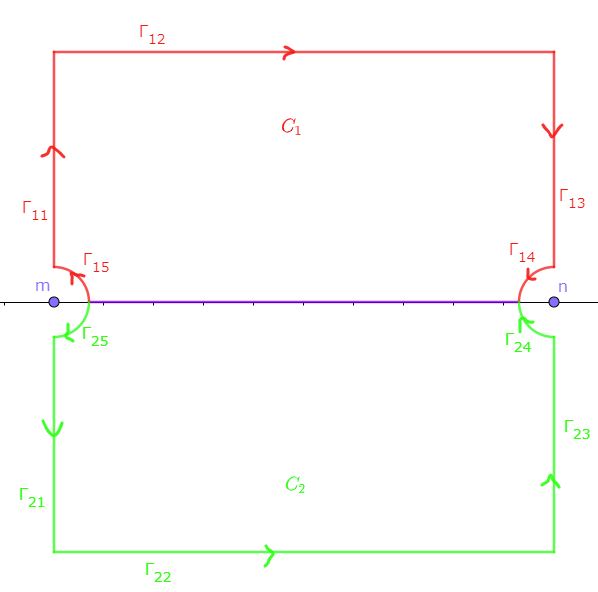
また $\mathfrak{I}z\ge0$ における積分路 $C_1$ は$$C_1=\G_{15}+\G_{11}+\G_{12}+\G_{13}+\G_{14}$$と定義します(赤色の経路)。同様に $\mathfrak{I}z\le0$ における緑色の積分路 $C_2$ を$$C_2=\G_{25}+\G_{21}+\G_{22}+\G_{23}+\G_{24}$$とすれば$$C=C_1-C_2$$であることが分かります。
実軸近辺で半円がくり抜かれています。これは(1)の被積分関数が $z\in\ZZ$ で極をもつために避けています。半径 $\epsilon$ の小さな半円であることに留意します。
$\G_{12}$ と $\G_{22}$ では $z$ の虚部(の絶対値)が非常に大きいと考えてください。
留数で積分値を求める
さて、(1)の被積分関数は $\cot$ のせいで $z=0,\pm1,\pm2\cdots$ において1位の極をもちます。$z=k\in\ZZ$ における留数は\begin{eqnarray*}\displaystyle\lim_{z\to k}f(z)\pi\cot\pi z\cdot(z-k)&=&\displaystyle\lim_{z\to k}f(z)\cos\pi z\frac{\pi(z-k)}{\sin\pi z}\\&=&\displaystyle\lim_{z\to k}f(z)\cos\pi z\frac{\pi(z-k)}{\sin\pi(z-k)}\cos k\pi\\&=&f(k)\end{eqnarray*}閉曲線 $C$ 内の極は $z=m+1,m+2,\cdots,n-1$ ですから、留数定理により$$\oint_Cf(z)\pi\cot\pi zdz=2\pi i\sum_{k=m+1}^{n-1}f(k)$$
\begin{equation}\therefore\quad\int_{C_2-C_1}f(z)\cot\pi zdz=2 i\sum_{k=m+1}^{n-1}f(k)\tag{2}\end{equation}
計算できる形づくり
(2)の左辺を変形しましょう。
\begin{eqnarray*}\int_{C_2-C_1}f(z)\cot\pi zdz&=&-\int_{C_1}f(z)\cot\pi zdz+\int_{C_2}f(z)\cot\pi zdz\\&=&-i\int_{C_1}f(z)(1-i\cot\pi z)dz-i\int_{C_2}f(z)(1+i\cot\pi z)dz\\&&+i\int_{C_1}f(z)dz+i\int_{C_2}f(z)dz\end{eqnarray*}$f(z)$ は正則なので周回積分するとゼロになることから$$\int_{C_1}f(z)dz+\int_{n-\epsilon}^{m+\epsilon}f(z)dz=0$$$$\int_{C_2}f(z)dz+\int_{n-\epsilon}^{m+\epsilon}f(z)dz=0$$これを先ほどの式に用いて\begin{eqnarray*}&&\int_{C_2-C_1}f(z)\cot\pi zdz\\&=&-i\int_{C_1}f(z)(1-i\cot\pi z)dz-i\int_{C_2}f(z)(1+i\cot\pi z)dz+2i\int_m^nf(z)dz\end{eqnarray*}ただし $\epsilon\to0$ としました(最後にまとめて極限をとるべきところですが、結果に影響しません)。
\begin{equation}\oint_{C}f(z)\cot\pi zdz=-i\int_{C_1}f(z)(1-i\cot\pi z)dz-i\int_{C_2}f(z)(1+i\cot\pi z)dz+2i\int_m^nf(z)dz\tag{3}\end{equation}
$C_1$の計算
(3)の $C_1$ の積分の被積分関数を評価します。\begin{eqnarray*}|1-i\cot\pi z|&=&\left|\frac{2e^{i\pi z}}{e^{i\pi z}-e^{-i\pi z}}\right|\\&=&\frac{2}{|1-e^{-2i\pi z}|}\\&=&\frac{2}{|1-e^{-2i\pi (x+iy)}|}\quad(z=x+iy)\\&=&\frac{2}{\sqrt{1-2e^{2\pi y}\cos2\pi x+e^{4\pi y}}}\\&\le&\frac{2}{\sqrt{1-2e^{2\pi y}+e^{4\pi y}}}\\&=&\frac{2}{e^{2\pi y}-1}\end{eqnarray*}$C_1$ は上半平面なので $y>0$ であることに注意します。$f(z)$ は有界ですから\begin{equation}|f(z)(1-i\cot\pi z)|\xrightarrow[]{y\to\infty}0\tag{4}\end{equation}となります。
実際に計算を進めます。$$\int_{C_1}f(z)(1-i\cot\pi z)dz=\int_{\G_{15}}+\int_{\G_{11}}+\int_{\G_{12}}+\int_{\G_{13}}+\int_{\G_{14}}$$(4)より $\G_{12}$ での虚部を $+\infty$ とする極限で $\int_{\G_{12}}\to0$ ですから$$\int_{C_1}f(z)(1-i\cot\pi z)dz=\int_{\G_{15}}+\int_{m+i\epsilon}^{m+i\infty}+\int_{n+i\infty}^{n+i\epsilon}+\int_{\G_{14}}$$$z=x+iy$ として\begin{eqnarray*}&=&i\int_{\epsilon}^{\infty}f(m+iy)(1-i\cot\pi(m+iy))dy\\&&-i\int_{\epsilon}^{\infty}f(n+iy)(1-i\cot\pi(n+iy))dy+\int_{\G_{14}}+\int_{\G_{15}}\\&=&i\int_{\epsilon}^{\infty}f(m+iy)(1-i\cot(i\pi y))dy\\&&-i\int_{\epsilon}^{\infty}f(n+iy)(1-i\cot(i\pi y))dy+\int_{\G_{14}}+\int_{\G_{15}}\\&=&i\int_{\epsilon}^{\infty}f(m+iy)\frac{-2}{e^{2\pi y}-1}dy\\&&-i\int_{\epsilon}^{\infty}f(n+iy)\frac{-2}{e^{2\pi y}-1}dy+\int_{\G_{14}}+\int_{\G_{15}}\end{eqnarray*}よって\begin{eqnarray*}&&\int_{C_1}f(z)(1-i\cot\pi z)dz\\&=&\frac{2}{i}\int_0^{\infty}\frac{f(m+iy)-f(n+iy)}{e^{2\pi y}-1}dy+\int_{\G_{14}}+\int_{\G_{15}}\end{eqnarray*}
$\G_{14}$ と $\G_{15}$は小さな円弧です。半径 $\epsilon\to0$ なら積分路はいくらでも短くなります。また $f(z)$ は有界でしたから $\int f(z)dz\to0$ となります。よって$$\int_{\G_{14}}f(z)(1-i\cot\pi z)dz=\frac{1}{i}\int_{\G_{14}}f(z)\cot\pi zdz$$$$\int_{\G_{15}}f(z)(1-i\cot\pi z)dz=\frac{1}{i}\int_{\G_{15}}f(z)\cot\pi zdz$$従って次の式を得ます。
\begin{eqnarray}\int_{C_1}&f(z)&(1-i\cot\pi z)dz\\&=&\frac{2}{i}\int_0^{\infty}\frac{f(m+iy)-f(n+iy)}{e^{2\pi y}-1}dy\\&&+\frac{1}{i}\int_{\G_{14}}f(z)\cot\pi zdz+\frac{1}{i}\int_{\G_{15}}f(z)\cot\pi zdz\tag{5}\end{eqnarray}
$C_2$の計算
同様にこちらも進めましょう。$z=x+iy$ とすると $y<0$ であることに注意します。\begin{eqnarray*}|1+i\cot\pi z|&=&\frac{2}{|e^{2i\pi z}-1|}\\&\le&\frac{2}{e^{-2\pi y}-1}\end{eqnarray*}$f(z)$ は有界ですから$$|f(z)(1+i\cot\pi z)|\xrightarrow[]{y\to -\infty}0$$となります。
$$\int_{C_2}f(z)(1+i\cot\pi z)dz=\int_{\G_{25}}+\int_{\G_{21}}+\int_{\G_{22}}+\int_{\G_{23}}+\int_{\G_{24}}$$$\G_{22}$ での虚部を $-\infty$ とする極限で $\int_{\G_{22}}\to0$ ですから$$\int_{C_2}f(z)(1+i\cot\pi z)dz=\int_{\G_{25}}+\int_{m-i\epsilon}^{m-i\infty}+\int_{n-i\infty}^{n-i\epsilon}+\int_{\G_{24}}$$$z=x+iy$ として\begin{eqnarray*}&=&-i\int_{\epsilon}^{\infty}f(m-iy)(1+i\cot\pi(m-iy))dy\\&&+i\int_{\epsilon}^{\infty}f(n-iy)(1+i\cot\pi(n-iy))dy+\int_{\G_{24}}+\int_{\G_{25}}\\&=&-i\int_{\epsilon}^{\infty}f(m-iy)(1-i\cot(i\pi y))dy\\&&+i\int_{\epsilon}^{\infty}f(n-iy)(1-i\cot(i\pi y))dy+\int_{\G_{24}}+\int_{\G_{25}}\\&=&-i\int_{\epsilon}^{\infty}f(m-iy)\frac{-2}{e^{2\pi y}-1}dy\\&&+i\int_{\epsilon}^{\infty}f(n-iy)\frac{-2}{e^{2\pi y}-1}dy+\int_{\G_{24}}+\int_{\G_{25}}\end{eqnarray*}よって\begin{eqnarray*}&&\int_{C_2}f(z)(1+i\cot\pi z)dz\\&=&\frac{2}{i}\int_0^{\infty}\frac{f(n-iy)-f(m-iy)}{e^{2\pi y}-1}dy+\int_{\G_{24}}+\int_{\G_{25}}\end{eqnarray*}
$\G_{24}$ と $\G_{25}$ については $\int f(z)dz\to0$ です。$$\int_{\G_{24}}f(z)(1+i\cot\pi z)dz=\frac{-1}{i}\int_{\G_{24}}f(z)\cot\pi zdz$$$$\int_{\G_{25}}f(z)(1+i\cot\pi z)dz=\frac{-1}{i}\int_{\G_{25}}f(z)\cot\pi zdz$$従って次の式を得ます。
\begin{eqnarray}\int_{C_2}&f(z)&(1+i\cot\pi z)dz\\&=&\frac{2}{i}\int_0^{\infty}\frac{f(n-iy)-f(m-iy)}{e^{2\pi y}-1}dy\\&&-\frac{1}{i}\int_{\G_{24}}f(z)\cot\pi zdz-\frac{1}{i}\int_{\G_{25}}f(z)\cot\pi zdz\tag{6}\end{eqnarray}
ここまでのまとめ
(5)(6)を(3)へ代入します。\begin{eqnarray*}\oint_{C}f(z)\cot\pi zdz&=&2i\int_m^nf(z)dz-2\int_0^{\infty}\frac{f(m+iy)-f(n+iy)}{e^{2\pi y}-1}dy\\&&-\int_{\G_{14}}f(z)\cot\pi zdz-\int_{\G_{15}}f(z)\cot\pi zdz\\&&-2\int_0^{\infty}\frac{f(n-iy)-f(m-iy)}{e^{2\pi y}-1}dy\\&&+\int_{\G_{24}}f(z)\cot\pi zdz+\int_{\G_{25}}f(z)\cot\pi zdz\\&=&2i\int_m^nf(z)dz\\&&-2\int_0^{\infty}\frac{f(m+iy)-f(m-iy)-f(n+iy)+f(n-iy)}{e^{2\pi y}-1}dy\\&&-\int_{\G_{14}}f(z)\cot\pi zdz-\int_{\G_{15}}f(z)\cot\pi zdz\\&&+\int_{\G_{24}}f(z)\cot\pi zdz+\int_{\G_{25}}f(z)\cot\pi zdz\end{eqnarray*}
\begin{eqnarray}&&\oint_{C}f(z)\cot\pi zdz\\&=&2i\int_m^nf(z)dz\\&&-2\int_0^{\infty}\frac{f(m+iy)-f(m-iy)-f(n+iy)+f(n-iy)}{e^{2\pi y}-1}dy\\&&-\int_{\G_{14}}f(z)\cot\pi zdz-\int_{\G_{15}}f(z)\cot\pi zdz\\&&+\int_{\G_{24}}f(z)\cot\pi zdz+\int_{\G_{25}}f(z)\cot\pi zdz\tag{7}\end{eqnarray}
ここからは、下2行の積分をどうにかしましょう。
経路の合体
経路の図を見ると $\G_{24}-\G_{14}$ は $n$ を中心とした半円を描きます。$$\int_{\G{24}}-\int_{\G{14}}=\int_{n\curvearrowright}$$円弧の角度は $\frac{3}{2}\pi$ から $\frac{\pi}{2}$ までなので $\curvearrowright$ の記号を+90度回して表示したいのですが、うまくいかないのでこれでいきます。同様に$$\int_{\G{25}}-\int_{\G{15}}=\int_{m\curvearrowright}$$この円弧は $\frac{\pi}{2}$ から $-\frac{\pi}{2}$ です。
したがって(7)式を書き改めると
\begin{eqnarray}&&\oint_{C}f(z)\cot\pi zdz\\&=&2i\int_m^nf(z)dz\\&&-2\int_0^{\infty}\frac{f(m+iy)-f(m-iy)-f(n+iy)+f(n-iy)}{e^{2\pi y}-1}dy\\&&+\int_{n\curvearrowright}f(z)\cot\pi zdz+\int_{m\curvearrowright}f(z)\cot\pi zdz\tag{8}\end{eqnarray}
半円の積分値
$$\int_{n\curvearrowright}f(z)\cot\pi z$$ で $z=n+\epsilon e^{i\theta}$ と置換すると\begin{eqnarray*}\int_{n\curvearrowright}f(z)\cot\pi z&=&\int_{\frac{3}{2}\pi}^{\frac{\pi}{2}}f(n+\epsilon e^{i\theta})\cot(\pi\epsilon e^{i\t})i\epsilon e^{i\t}d\t\\&=&i\epsilon\int_{\frac{3}{2}\pi}^{\frac{\pi}{2}}f(n)\cot(\pi\epsilon e^{i\t})e^{i\t}d\t\end{eqnarray*}$\phi=\t-\pi$ と置換してまた $\t$ と書き直すと$$=i\epsilon\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}f(n)\cot(\pi\epsilon e^{i\t})e^{i\t}d\t$$よって $\int_{n\curvearrowright}$ の値は $n$ を時計回りに1周した値の半分です。すなわち留数の半分を考えればよく、$$\int_{n\curvearrowright}f(z)\cot\pi z=-if(n)$$($f(z)\pi\cot\pi z$ の留数が $f(n)$ なので。また積分は時計回りであったことに注意)。
$\int_{m\curvearrowright}$ についても同様にやれば(8)式は次のようになります。
\begin{eqnarray}&&\oint_{C}f(z)\cot\pi zdz\\&=&2i\int_m^nf(z)dz\\&&-2\int_0^{\infty}\frac{f(m+iy)-f(m-iy)-f(n+iy)+f(n-iy)}{e^{2\pi y}-1}dy\\&&-if(n)-if(m)\tag{9}\end{eqnarray}
冒頭の(2)式を再掲します。$$\int_{C_2-C_1}f(z)\cot\pi zdz=2 i\sum_{k=m+1}^{n-1}f(k)$$$C_2-C_1=C$ ですから$$2 i\sum_{k=m+1}^{n-1}f(k)=\oint_{C}f(z)\cot\pi zdz$$(9)をガツンと代入します。\begin{eqnarray*}&&2 i\sum_{k=m+1}^{n-1}f(k)\\&=&2i\int_m^nf(z)dz\\&&-2\int_0^{\infty}\frac{f(m+iy)-f(m-iy)-f(n+iy)+f(n-iy)}{e^{2\pi y}-1}dy\\&&-if(n)-if(m)\end{eqnarray*}$2i$ で割って\begin{eqnarray*}&&\sum_{k=m+1}^{n-1}f(k)\\&=&\int_m^nf(z)dz\\&&+i\int_0^{\infty}\frac{f(m+iy)-f(m-iy)-f(n+iy)+f(n-iy)}{e^{2\pi y}-1}dy\\&&-\frac{f(m)+f(n)}{2}\end{eqnarray*}両辺に $f(m)+f(n)$ を加算すれば公式の完成!
\begin{multline}\sum_{k=m}^nf(k)=\frac{f(m)+f(n)}{2}+\int_m^nf(z)dz\\+i\int_0^\infty\frac{f(m+iy)-f(m-iy)-f(n+iy)+f(n-iy)}{e^{2\pi y}-1}dy\end{multline}
不慣れな計算だったので自分としては骨が折れました。参考になったのは意外にも日本語版Wikipediaです。英語版より詳しい。
プラナの論文も見てみたのですが、イタリア語だか何なのか全く読めませんでした。
この公式は後日ガンマ関数に関する「ビネの第2公式」を証明するときに使います。というかそのためにこれをやった感じです。
→やりました:
アベル・プラナの和公式のバリエーション:
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。




