アベル・プラナの和公式のバリエーション（複素積分・cotでなくtanで導出する）

以前、アベル・プラナの和公式（Abel-Plana summation formula）を導出しました。

2022年3月5日 アベル・プラナの和公式　複素積分を応用して

その公式は以下で表されます。

今回はこれの少し変化したバージョンをやります。

これに取り組んだのは、とある積分を計算するときにアベル・プラナの和公式の $e^{2\pi y} -1$ の部分が $e^{2\pi y} +1$ となった公式が欲しいなと思ったのがきっかけです。

導出の仕方はアベル・プラナの和公式とほとんど同じで、かつそれよりもお手軽です。では見ていきましょう。

複素積分と留数

$m\le n\in\ZZ$ とします。関数 $f(z)$ は $m\le\mathfrak{R}z\le n$ で有界かつ正則します。さらに周回積分 $$\oint_C f(z)\tan\pi zdz$$ を考えます（アベル・プラナの和公式のときは $\cot\pi z$ でした）。積分路は下図です。

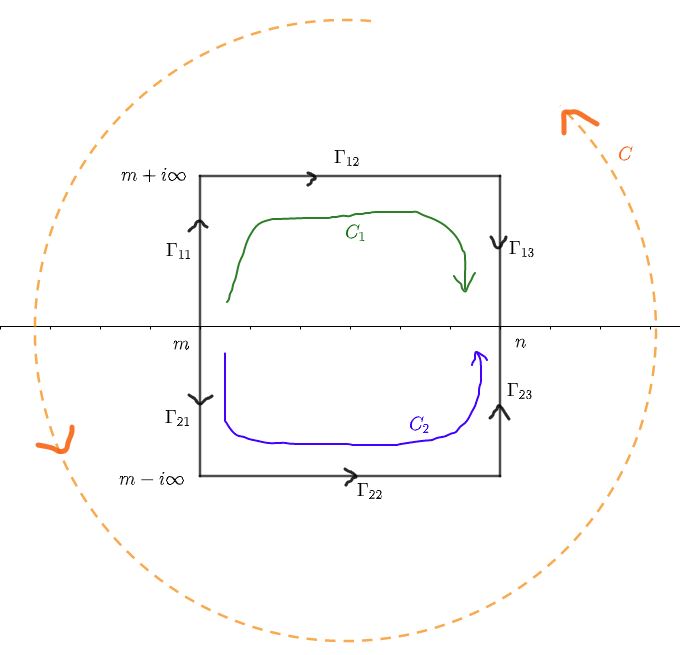
縦に長い長方形の周回 $C$ は上半分の経路 $C_1$ と下半分の経路 $C_2$ の組み合わせですが、向きに注意します。 $$\begin{cases}C&=&C_2-C_1\\C_1&=&\G_{11}+\G_{12}+\G_{13}\\C_2&=&\G_{21}+\G_{22}+\G_{23}\end{cases}$$

被積分関数は $\pm\frac{1}{2},\pm\frac{3}{2},\pm\frac{5}{2},\cdots$ に1位の極をもちますので、留数により積分値を求めます。 $$\begin{eqnarray*}\oint_C f(z)\tan\pi zdz&&=2\pi i\sum_{k=m}^{n-1}\displaystyle\lim_{z\to k+\frac{1}{2}}f(z)\tan\pi z\cdot \left(z-k-\frac{1}{2}\right)\\&&=2\pi i\sum_{k=m}^{n-1}\displaystyle\lim_{z\to k}f\left(z+\frac{1}{2}\right)\tan\pi (z+1/2)\cdot (z-k)\\&&=2\pi i\sum_{k=m}^{n-1}\displaystyle\lim_{z\to k}f\left(z+\frac{1}{2}\right)\frac{\cos\pi z}{-\sin \pi z}\cdot (z-k)\\&&=-2i\sum_{k=m}^{n-1}\displaystyle\lim_{z\to k}f\left(z+\frac{1}{2}\right)\cos\pi z\frac{\pi(z-k)}{\sin \pi (z-k)}(-1)^k\\&&=-2i\sum_{k=m}^{n-1}f\left(k+\frac{1}{2}\right)\end{eqnarray*}$$

したがって次のようになります。

積分路の分割と賢い変形

(1)の左辺は $$\oint_C f(z)\tan\pi zdz=\int_{C_2} f(z)\tan\pi zdz-\int_{C_1} f(z)\tan\pi zdz$$ アベル・プラナの和公式を導出したときを思い出しながら、やや技巧的な変形をしていきます。

$$\begin{eqnarray*}\oint_C f(z)\tan\pi zdz&&=-i\int_{C_1}f(z)dz-i\int_{C_2}f(z)dz\\&&\quad-i\int_{C_2}f(z)(i\tan\pi z-1)dz+i\int_{C_1}f(z)(i\tan\pi z+1)dz\end{eqnarray*}$$

$f(z)$ は正則なので右辺第1,2項は経路を変形できます。 $$\int_{C_1}f(z)dz=\int_{C_2}f(z)dz=\int_m^n f(x)dx$$ したがって

右辺第2項について

(2)の右辺第2項は経路 $C_2$ ですので $z=x+iy$ と表したときに $y\le0$ です。よって $$\begin{eqnarray*}|i\tan\pi z-1|&&=\left|\frac{e^{i\pi z}-e^{-i\pi z}}{e^{i\pi z}+e^{-i\pi z}}-1\right|\\&&=\frac{2}{|e^{2i\pi z}+1|}\\&&=\frac{2}{|e^{2i\pi x}e^{-2\pi y}+1|}\\&&\le\frac{2}{|e^{-2\pi y}-1|}\\&&\xrightarrow[y\to-\infty]{}0\end{eqnarray*}$$ $f(z)$ は有界だと仮定していますから $$|f(z)(i\tan\pi z-1)|\xrightarrow[y\to-\infty]{}0$$ よって経路 $C_2$ のうち $\G_{22}$ の積分値はゼロとなります。

$$\begin{eqnarray*}\int_{C_2}&&f(z)(i\tan\pi z-1)dz\\&&=\int_{\G_{21}}+\int_{\G_{23}}\\&&=-i\int_0^\infty f(m-iy)\bigl(i\tan\pi(m-iy)-1\bigr)dy\\&&\quad -i\int_\infty^0f(n-iy)\bigl(i\tan\pi(n-iy)-1\bigr)dy\\&&=i\int_0^\infty f(m-iy)(i\tan i\pi y+1)dy\\&&\quad +i\int_\infty^0f(n-iy)(i\tan i\pi y+1)dy\\&&=i\int_0^\infty \Bigl(f(m-iy)-f(n-iy)\Bigr)(i\tan i\pi y+1)dy\\&&=2i\int_0^\infty \frac{f(m-iy)-f(n-iy)}{e^{2\pi y}+1}dy\end{eqnarray*}$$

右辺第3項について

(2)の右辺第3項は経路 $C_1$ ですので $y\ge0$ です。 $$\begin{eqnarray*}|i\tan\pi z+1|&&=\left|\frac{e^{i\pi z}-e^{-i\pi z}}{e^{i\pi z}+e^{-i\pi z}}+1\right|\\&&=\frac{2}{|e^{-2i\pi z}+1|}\\&&=\frac{2}{|e^{-2i\pi x}e^{2\pi y}+1|}\\&&\le\frac{2}{|e^{2\pi y}-1|}\\&&\xrightarrow[y\to +\infty]{}0\end{eqnarray*}$$ $f(z)$ は有界だと仮定していますから $$|f(z)(i\tan\pi z+1)|\xrightarrow[y\to+\infty]{}0$$ よって経路 $C_1$ のうち $\G_{12}$ の積分値はゼロとなります。

$$\begin{eqnarray*}\int_{C_1}&&f(z)(i\tan\pi z+1)dz\\&&=\int_{\G_{11}}+\int_{\G_{13}}\\&&=i\int_0^\infty f(m+iy)\bigl(i\tan\pi(m+iy)+1\bigr)dy\\&&\quad +i\int_\infty^0f(n+iy)\bigl(i\tan\pi(n+iy)+1\bigr)dy\\&&=i\int_0^\infty f(m+iy)(i\tan i\pi y+1)dy\\&&\quad +i\int_\infty^0f(n+iy)(i\tan i\pi y+1)dy\\&&=i\int_0^\infty \Bigl(f(m+iy)-f(n+iy)\Bigr)(i\tan i\pi y+1)dy\\&&=2i\int_0^\infty \frac{f(m+iy)-f(n+iy)}{e^{2\pi y}+1}dy\end{eqnarray*}$$

公式の完成

(3)(4)を(2)へ用いると $$\begin{eqnarray*}\oint_C f(z)\tan\pi zdz&=&-2i\int_m^nf(x)dx\\&&+2\int_0^\infty \frac{f(m-iy)-f(n-iy)}{e^{2\pi y}+1}dy\\&&-2\int_0^\infty \frac{f(m+iy)-f(n+iy)}{e^{2\pi y}+1}dy\end{eqnarray*}$$ 左辺を(1)によって書き換えれば求めていた公式を得ます。

特別な場合

$m=0$ , $n\to\infty$ とすると $$\begin{multline}\sum_{k=0}^\infty f\left(k+\frac{1}{2}\right)=\int_0^\infty f(x)dx\\+i\displaystyle\lim_{n\to\infty}\int_0^\infty\frac{f(-iy)-f(iy)-f(n-iy)+f(n+iy)}{e^{2\pi y}+1}dy\end{multline}$$ $f(z)$ が $$\displaystyle\lim_{n\to\infty}\int_0^\infty\frac{f(n\pm iy)}{e^{2\pi y}+1}dy=0$$ を満たすような関数である場合には

これだとシンプルで応用がしやすそうですね。

応用例（ディガンマ関数/ビネの第2公式の類似）

$$f(\a)=\frac{1}{(z+\a)^2}$$ とすると $$\sum_{n=0}^{\infty}\frac{1}{(z+n+\frac{1}{2})^2}=\int_0^\infty \frac{dx}{(z+x)^2}+i\int_0^\infty\frac{(z-iy)^{-2}-(z+iy)^{-2}}{e^{2\pi y}+1}dy$$ 左辺はディガンマ関数の微分（あるいはフルヴィッツゼータ関数）です。右辺も整理して

なる積分表示を得ます。ここ以降は

【γ19】対数ガンマ関数におけるビネの第2公式の導出（アベル・プラナの和公式,ポリガンマ関数）（ガンマ関数の基礎19）

を参考に、ビネの第2公式の類似公式を導きましょう。(7)を $1$ から $z$ まで積分すると $$\begin{equation}\psi\left(z+\frac{1}{2}\right)=\ln z+2\int_0^\infty\frac{ydy}{(y^2+z^2)(e^{2\pi y}+1)}+C\tag{8}\end{equation}$$ ただし $C$ は定数をまとめたものです。(8)を $1$ から $z$ まで積分して $$\begin{eqnarray*}\ln\G\left(z+\frac{1}{2}\right) &=& \ln\G\left(\frac{3}{2}\right)+z\ln z+(C-1)z+1-C\\&&+2\int_0^\infty\frac{\arctan\frac{z}{y}-\arctan\frac{1}{y}}{e^{2\pi y}+1} \\&=&\ln\G\left(\frac{3}{2}\right)+z\ln z+(C-1)z+1-C\\&&+2\int_0^\infty\frac{\arctan y -\arctan\frac{y}{z}}{e^{2\pi y}+1}dy\end{eqnarray*}$$ 最後の変形は $\arctan X=\frac{\pi}{2}-\arctan \frac{1}{X}$ を考えるといいです。よって定数項を $C'$ とすると $$\begin{equation}\ln\G\left(z+\frac{1}{2}\right)=z\ln z+(C-1)z+C'-2\int_0^\infty\frac{\arctan\frac{y}{z}}{e^{2\pi y}+1}dy\tag{9}\end{equation}$$ 積分（ログガンマの剰余項にあたる）を評価します。 $$\begin{eqnarray*}\left|\ln\G\left(z+\frac{1}{2}\right)-z\ln z-(C-1)z-C'\right|&=& 2\left|\int_0^\infty\frac{\arctan\frac{y}{z}}{e^{2\pi y}+1}dy\right|\\&\le&\frac{2}{z}\int_0^\infty\frac{ydy}{e^{2\pi y}+1}\\&=&\frac{96}{z}\xrightarrow[z\to\infty]{}0\end{eqnarray*}$$ 最後の計算はゼータ関数の積分表示を参照。 $$\therefore\quad \ln\G\left(z+\frac{1}{2}\right)-z\ln z-(C-1)z-C'\xrightarrow[z\to\infty]{}0$$ 左辺を変形します。 $$\begin{eqnarray*}&&\left[\ln\G\left(z+\frac{1}{2}\right)-z\ln\left(z+\frac{1}{2}\right)+z+\frac{1}{2}-\frac{\ln2\pi}{2}\right]\\&&+z\left\{\ln\left(1+\frac{1}{2z}\right)-C\right\}+\frac{\ln2\pi}{2}-\frac{1}{2}-C'\xrightarrow[z\to\infty]{}0\end{eqnarray*}$$ 1行目大括弧の中身はビネの第2公式の導出の際に得た $$\displaystyle\lim_{z\to\infty}\left|\log\G(z)-\left(z-\frac{1}{2}\right)\log z+z-\frac{\ln2\pi}{2}\right|=0$$ によって消えます。 $$\therefore\quad z\left\{\ln\left(1+\frac{1}{2z}\right)-C\right\}+\frac{\ln2\pi}{2}-\frac{1}{2}-C'\xrightarrow[z\to\infty]{}0$$ $$\Rightarrow -Cz+\frac{1}{2}\ln\left(1+\frac{1}{2z}\right)^{2z}+\frac{\ln2\pi}{2}-\frac{1}{2}-C'\xrightarrow[z\to\infty]{}0$$ $$\Rightarrow -Cz+\frac{\ln2\pi}{2}-C'\xrightarrow[z\to\infty]{}0$$ これを満たすには $C=0$ , $C'=\frac{\ln2\pi}{2}$ でなくてはなりません。

したがって(8)(9)式は次のようになります。

特に $z=1$ なら

アベル・プラナの和公式を応用した記事：

2022年3月6日 【γ19】対数ガンマ関数におけるビネの第2公式の導出（アベル・プラナの和公式,ポリガンマ関数）（ガンマ関数の基礎19）

複素積分演習：

2022年3月30日 複素積分演習（cos(log x)/(1+x^2)）

2022年1月25日 $\int\frac{dx}{(1+x^2)^{n+1}}$ 複素積分演習

応援のおねがい

Please support me!

まめしば

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。

ご支援いただいた方は、こちらで確認できます。

◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。

◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。

◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。