前回はこちら:
\begin{equation}I:=\int_0^\frac{\pi}{2}\ln(\ln^2\cos\t+\t^2) d\t =\pi\ln\ln 2\tag{1.1}\end{equation}類似の問題として\begin{eqnarray}\int_0^\pi \ln(\ln^2\sin\t+\t^2) d\t &=&\pi\ln\left(\ln^2 2+\frac{\pi^2}{4}\right)\tag{1.2}\\\int_0^\pi \arctan\frac{\ln\sin\t}{\t}d\t&=&-\pi\arctan\frac{2\ln 2}{\pi}\tag{1.3}\end{eqnarray}さらに類似の問題として\begin{equation}\int_0^\frac{\pi}{2}\frac{\cos(2s\arctan\frac{x}{\ln\cos x})}{(\ln^2\cos x+x^2)^s}dx=\frac{\pi}{2\ln^{2s}2}\tag{1.4}\end{equation}$$\int_0^\frac{\pi}{2}\frac{\ln\cos x}{x^2+\ln^2\cos x}dx=\frac{\pi}{2}\left(1-\frac{1}{\ln 2}\right)$$
(1.1)(1.4)は積分botで現れた式です。左辺を見ると、$\t=0$ で被積分関数の外側の $\ln$ が発散し、$\t=\pi/2$ で内側の $\ln$ が発散しています。よってこれは広義積分です。wolframで計算すると収束します。
また(1.2)(1.3)は@6ahRJ6PeIkQWmsk さんからの問題を少し広げたものです。
対数の中に対数がある場合の対応として、対数を1つ消してしまうことが考えられます。例えば部分積分を用いれば、対数を微分できますが、今回の場合はあまりに複雑になってしまいます。もう1つの方法として指数のパラメータを導入します。$f(x)^s$ を $s$ で微分すると $f(x)^s\ln f(x)$ となり、$s=0$ として $\ln f(x)$ が得られます。つまり$$I(s):=\int_0^\frac{\pi}{2}(\ln^2\cos\t+\t^2)^s d\t$$として $I(s)$ を計算して微分するのです。これは十分試す価値こそあるものの、ここでは採用しません。
対数を消すことをあきらめるならば、留数定理が有効でしょう。複素解析に持ち込むならば、実関数の積分である $I$ を出現させる複素関数 $f(z)$ を探す必要があります。そこで(1)の被積分関数を変形して$$\ln(\ln\cos\t+i\t)+\ln(\ln\cos\t-i\t)$$としてみます。2つの項は互いに複素共役ですから$$\ln(\ln^2\cos\t+\t^2)=2\mathfrak{R}\ln(\ln\cos\t+i\t)$$すなわち $\ln(\ln\cos\t+i\t)$ を積分できればよいです。オイラーの公式によって$$\ln(\ln\cos\t+i\t)=\ln(\ln\frac{e^{2i\t}+1}{2})$$積分の変数変換で角度を半分にすれば $e^{i\t}$ の関数となります。したがって $z=e^{i\t}$ として円を周る複素積分に帰着することが分かります。これを踏まえてやっていきましょう。
$\mathrm{Log}$ は主値における複素対数を表し、$\ln$ を正の真数の対数とします(要は高校のと同じ)。\begin{equation}f(z):=\frac{1}{z}\mathrm{Log'}\left(\mathrm{Log}\frac{1+z}{2}\right)\tag{2}\end{equation}として $\displaystyle\oint f(z)dz$ を考えます。ただし内側の対数 $\mathrm{Log}$ の偏角を $(-\pi,\pi]$ に、外側の対数 $\mathrm{Log'}$ の偏角を $[0,2\pi)$ に限定します。経路 $C$ は半径 $1$ の円ですが、$z=\pm 1$ を小さな半円でくり抜きます。
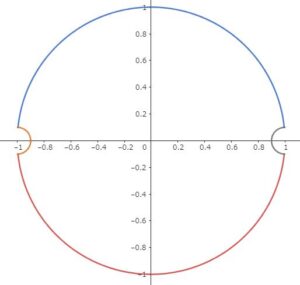
どうしてそんなにややこしい設定なのか。それは円の経路を取るために仕方ないのです。
まず内側の対数 $\mathrm{Log}\frac{1+z}{2}$ について、$z=-1$ が分岐点(branch point)となっています。よってここでは、正則でないので経路から外す必要があるのみならず、切断(branch cut)を入れねばなりません。$\mathrm{Log}\: z$ の偏角は $(-\pi,\pi]$ に限定されていますので、$\mathrm{Log}\: z$ は負の実軸上で不連続であり、ここに切断を入れます。つまり今の場合は $\frac{1+x}{2}\le 0$ となるような範囲、すなわち実軸の $(-\infty,-1]$ を切断します。
次に外側の対数 $\mathrm{Log'}$ について、$z=1$ が分岐点になっているので、同じく小円でくり抜いて切断を入れます。偏角の範囲が $[0,2\pi)$ ですので、$\mathrm{Log'}\:z$ は正の実軸上で不連続であり、ここに切断を入れます。つまり今の場合は $\mathrm{Log}\frac{1+x}{2}\ge 0$ となるような範囲、すなわち実軸の $[1,+\infty)$ を切断します。
$f(z)$ で怪しい点は $-1,1,0$ です。
まず $z=0$ は経路の内部の点であり、留数計算に関わってきます。メルカトル級数\begin{equation}\mathrm{Log}(1+z)=\sum_{n=1}^\infty\frac{(-1)^{n-1}}{n}z^n\tag{3}\end{equation}より $\mathrm{Log}(1+z)$ は $z=0$ で正則で、\begin{equation}\lim_{z\to 0}zf(z)=\mathrm{Log'}\left(\ln\frac{1}{2}\right)=\mathrm{Log'}(-\ln 2)=\ln\ln2+\pi i\tag{4}\end{equation}したがって $f(z)$ は $z=0$ に1位の極をもちます。
次に $z=1$ についてはwolframによると\begin{equation}\ln\ln\frac{1+x}{2}=\ln\frac{x-1}{2}-\frac{x-1}{4}+O((x-1)^2)\tag{5}\end{equation}であり、$z=1$ の近くでは $f(z)\approx \frac{\ln\frac{z-1}{2}}{z}$ となっています。
最後に $z=-1$ については、有効な漸近展開があるのかは分かりませんが、ここでは特に問題ありません。
留数定理より\begin{equation}\oint f(z)dz=2\pi i \mathrm{Log'}\mathrm{Log}\frac{1}{2}=2\pi i(\ln\ln 2+i\pi)\tag{6}\end{equation}これで周回積分の値は求まりました。
くり抜かれた2つの小半円を評価します。
まず $z=1+\epsilon e^{i\t}$ とすると(5)より、$z=-1$ まわりの小円の積分は\begin{eqnarray*}\left|\int f(z)dz\right|&=&\left|\int \left(\mathrm{Log'}\frac{\epsilon e^{i\t}}{2}-\frac{\epsilon e^{i\t}}{4}+O(\epsilon^2)\right)i\epsilon e^{i\t}d\t\right|\\ &\le&\int\left|\epsilon\ln\frac{\epsilon}{2}+i\epsilon\t+O(\epsilon^2)\right|d\t\\&\to& 0\quad(\epsilon\to 0)\end{eqnarray*}次に $z=-1+\epsilon e^{i\t}$ とすると、$z=1$ まわりの小円の積分は\begin{eqnarray*}\left|\int f(z)dz\right| &\le& \int_{-\frac{\pi}{2}}^\frac{\pi}{2}\left|\epsilon\mathrm{Log'}\mathrm{Log}\frac{\epsilon e^{i\t}}{2}\right|d\t \\&=&\int_{-\frac{\pi}{2}}^\frac{\pi}{2}\left|\epsilon\mathrm{Log'}\left(\ln\frac{\epsilon}{2}+i\t\right)\right|d\t \\&\to& 0\quad(\epsilon\to 0)\end{eqnarray*}
よって、共にゼロとなります。
残るは半径1の円です。$z=e^{i\t}$ とおけば$$\oint f(z)dz=i\int_0^\pi\mathrm{Log'}\mathrm{Log}\frac{1+e^{i\t}}{2}d\t+i\int_{-\pi}^0\mathrm{Log'}\mathrm{Log}\frac{1+e^{i\t}}{2}d\t$$第2項を $\t\to -\t$ と置換すると$$=i\int_0^\pi\left(\mathrm{Log'}\mathrm{Log}\frac{1+e^{i\t}}{2}+\mathrm{Log'}\mathrm{Log}\frac{1+e^{-i\t}}{2}\right)d\t$$ここで$$\frac{1+e^{\pm i\t}}{2}=\cos\frac{\t}{2}e^{\pm i\frac{\t}{2}}\Longrightarrow\mathrm{Log}\frac{1+e^{\pm i\t}}{2}=\ln\cos\frac{\t}{2}\pm i\frac{\t}{2}$$これをさらに変形して$$\mathrm{Log}\frac{1+e^{\pm i\t}}{2}=\sqrt{\ln^2\cos\frac{\t}{2}+\frac{\t^2}{4}}e^{\pm i\a}\quad,\quad \tan\a=\frac{\t/2}{\ln\cos\frac{\t}{2}}$$このとき $-\frac{\pi}{2}<\a <0$ を満たしています。よって $\mathrm{Log'}$ の偏角に注意すれば$$\oint f(z)dz=i\int_0^\pi\left[\mathrm{Log}\left(\sqrt{\ln^2\cos\frac{\t}{2}+\frac{\t^2}{4}}e^{i(\a+2\pi)}\right)+\mathrm{Log}\left(\sqrt{\ln^2\cos\frac{\t}{2}+\frac{\t^2}{4}}\:e^{- i\a}\right)\right]d\t$$$$\therefore\quad\oint f(z)dz=i\int_0^\pi\ln\left(\ln^2\cos\frac{\t}{2}+\frac{\t^2}{4}\right)d\t-2\pi^2=2i\int_0^\frac{\pi}{2}\left(\ln^2\cos\t+\t^2\right)d\t-2\pi^2$$
(6)と比べると
$$\int_0^\frac{\pi}{2}\ln(\ln^2\cos\t+\t^2) d\t =\pi\ln\ln 2$$
きれいなような、奇妙な感じのような結果です。
@6ahRJ6PeIkQWmsk さんからの問題です。少し改題。
$$\int_0^\pi \ln(\ln^2\sin\t+\t^2) d\t =\pi\ln\left(\ln^2 2+\frac{\pi^2}{4}\right)$$$$\int_0^\pi \arctan\frac{\ln\sin\t}{\t}d\t=-\pi\arctan\frac{2\ln 2}{\pi}$$
考える複素関数は$$g(z):=\frac{1}{z}\mathrm{Log'}\left(i\:\mathrm{Log}\frac{1-z}{2i}\right)$$$\mathrm{Log}$ および $\mathrm{Log'}$ の偏角の範囲を $[-\frac{3}{2}\pi , \frac{\pi}{2})$ とします。つまり $\mathrm{Log}w$ , $\mathrm{Log'}w$ の $w$ 平面での切断は $[0,+\infty)$ に入っています。今の場合、内側の $\mathrm{Log}\frac{1-z}{2i}$ の分岐点は $z=1$ であり、偏角を考えると、$z$ 平面における切断は $[1,+\infty)$ に入っていると分かります。外側の $\mathrm{Log}$ の分岐点は $z=1-2i$ です。ここで、その分岐点から $z$ 平面のどの方向へ切断が描かれるか考えます。$\mathrm{Log'}w$ における切断が $w=ia$ ($a\ge 0$)なので$$i\:\mathrm{Log}\frac{1-z}{2i}=ia\Rightarrow z=1-2e^a i\quad(a\ge 0)$$により、この切断は $z=1-2i$ から虚軸の負方向へ伸びています。
さて、積分経路は、原点中心で半径 $1$ の円から $z=1$ を小さな半円でくり抜いたものとします。もう1つの分岐点およびその切断は経路の外にあるので無視します。小さな半円は先ほどと同様に、積分がゼロと評価されますので、メインの円のみ考えればOK。
$z=0$ で1位の極をもつので、留数定理により$$\oint g(z)dz=\pi i\ln\left(\ln^2 2+\frac{\pi^2}{4}\right)+2\pi\arctan\frac{2\ln 2}{\pi}$$円に沿った積分は\begin{eqnarray*}\oint g(z)dz &=& i\int_0^{2\pi}\mathrm{Log'}\left(i\:\mathrm{Log}\frac{1-e^{i\t}}{2i}\right)d\t\\&=&2i\int_0^\pi\mathrm{Log'}\left(i\:\mathrm{Log}\frac{1-e^{2i\t}}{2i}\right)d\t \\&=& 2i\int_0^\pi\mathrm{Log'}\left(i\:\mathrm{Log}(-e^{i\t}\sin\t)\right)d\t\end{eqnarray*}$\mathrm{Log}$ の偏角を考慮して負号を極形式に置き換えます。\begin{eqnarray*} &=& 2i\int_0^\pi\mathrm{Log'}\left(i\:\mathrm{Log}(e^{i(\t-\pi)}\sin\t)\right)d\t \\&=& 2i\int_0^\pi\mathrm{Log'}(\pi-\t+i\ln\sin\t)d\t \\&=& 2i\int_0^\pi\mathrm{Log'}(\t+i\ln\sin\t)d\t\quad(\t\to\pi-\t)\\&=&i\int_0^\pi \ln(\ln^2\sin\t+\t^2) d\t-2\int_0^\pi \arctan\frac{\ln\sin\t}{\t}d\t\end{eqnarray*}したがって$$\int_0^\pi \ln(\ln^2\sin\t+\t^2) d\t =\pi\ln\left(\ln^2 2+\frac{\pi^2}{4}\right)$$$$\int_0^\pi \arctan\frac{\ln\sin\t}{\t}d\t=-\pi\arctan\frac{2\ln 2}{\pi}$$
$s<1/2$,\begin{equation}\int_0^\frac{\pi}{2}\frac{\cos(2s\arctan\frac{x}{\ln\cos x})}{(\ln^2\cos x+x^2)^s}dx=\frac{\pi}{2\ln^{2s}2}\end{equation}$s=1/2$ のときは$$\int_0^\frac{\pi}{2}\frac{\ln\cos x}{x^2+\ln^2\cos x}dx=\frac{\pi}{2}\left(1-\frac{1}{\ln 2}\right)$$
考える複素積分を$$\oint_C\left\{\mathrm{Log}\left(\frac{1+z}{2}\right)\right\}^{-2s}\frac{dz}{z}$$とし、周回経路は(2)をやったときと同じで、半径1の円の $z=\pm 1$ を小さくくり抜いたものです。平面の切断も同様で $(-\infty,-1]$ と $[1,+\infty)$ です。$\mathrm{Log}$ の主値の偏角を $(-\pi,\pi]$ に、 $(\quad)^{-2s}$ の主値の偏角を $[0,2\pi)$ に限定します(理由も全く同じ)。留数定理により$$\oint_C\left\{\mathrm{Log}\left(\frac{1+z}{2}\right)\right\}^{-2s}\frac{dz}{z}=2\pi i(-\ln 2)^{-2s}$$$(-\ln 2)^{-2s}=(e^{\pi i}\ln 2)^{-2s}$ なので$$\therefore\quad\oint_C\left\{\mathrm{Log}\left(\frac{1+z}{2}\right)\right\}^{-2s}\frac{dz}{z}=\frac{2\pi i e^{-2\pi si}}{\ln^{2s}2}$$くり抜いた小円の積分はゼロなので、半径1の円の積分のみ計算します。角度パラメータは $-\pi$ から $0$ と、$0$ から $\pi$ に分かれていますが、まとめて書きます。\begin{eqnarray*}\oint_C &=& i\int_{-\pi}^\pi\left\{\mathrm{Log}\left(\frac{1+e^{ix}}{2}\right)\right\}^{-2s}dx \\&=& 2i\int_{-\frac{\pi}{2}}^\frac{\pi}{2}\left\{\mathrm{Log}\left(\frac{1+e^{2ix}}{2}\right)\right\}^{-2s}dx\\&=&2i\int_{-\frac{\pi}{2}}^\frac{\pi}{2}\left\{\mathrm{Log}\left(\cos x\cdot e^{ix}\right)\right\}^{-2s}dx\end{eqnarray*}$x$ はその積分範囲では $\mathrm{Log}$ の主値の範囲に収まっているので\begin{eqnarray*} &=&2i\int_{-\frac{\pi}{2}}^\frac{\pi}{2}\left\{\ln\cos x+ix\right\}^{-2s}dx\\&=& 2i\int_{-\frac{\pi}{2}}^\frac{\pi}{2}\left(\sqrt{\ln^2\cos x+x^2}\:e^{i\arctan\frac{x}{\ln\cos x}}\right)^{-2s}dx\end{eqnarray*}$-\frac{\pi}{2}<\arctan\frac{x}{\ln\cos x}<0$ は$(\quad)^{-2s}$ の主値の範囲ではないので $2\pi$ を加えて偏角とします。\begin{eqnarray*} &=& 2i\int_{-\frac{\pi}{2}}^\frac{\pi}{2}\left(\sqrt{\ln^2\cos x+x^2}\:e^{i(2\pi+\arctan\frac{x}{\ln\cos x})}\right)^{-2s}dx\\&=&2ie^{-2\pi si}\int_{-\frac{\pi}{2}}^\frac{\pi}{2}\frac{e^{-2is\arctan\frac{x}{\ln\cos x}}}{(\ln^2\cos x+x^2)^s}dx\end{eqnarray*}留数定理の結果と合わせて$$\int_{-\frac{\pi}{2}}^\frac{\pi}{2}\frac{e^{-2is\arctan\frac{x}{\ln\cos x}}}{(\ln^2\cos x+x^2)^s}dx=\frac{\pi }{\ln^{2s}2}$$積分区間をちょうど半分に分けて、$x$ が負のほうで $x\to -x$ と置換すると$$\int_0^\frac{\pi}{2}\frac{e^{2is\arctan\frac{x}{\ln\cos x}}+e^{-2is\arctan\frac{x}{\ln\cos x}}}{(\ln^2\cos x+x^2)^s}dx=\frac{\pi }{\ln^{2s}2}$$$$\therefore\quad\int_0^\frac{\pi}{2}\frac{\cos(2s\arctan\frac{x}{\ln\cos x})}{(\ln^2\cos x+x^2)^s}dx=\frac{\pi}{2\ln^{2s}2}$$
なお、$s=1/2$ のときは $z=1$ が極となるため、留数の半分を加える必要があります(主値積分)。
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。