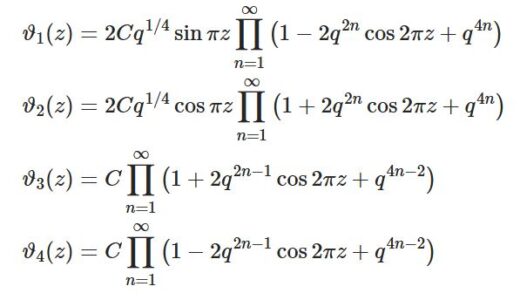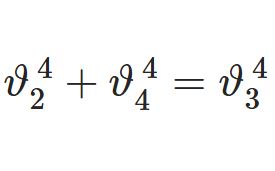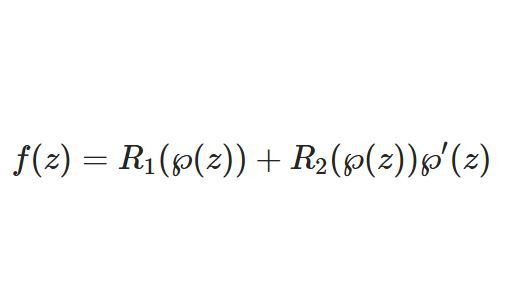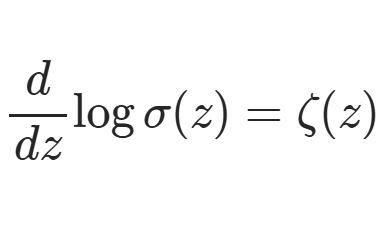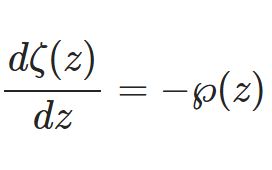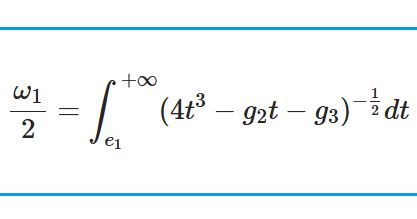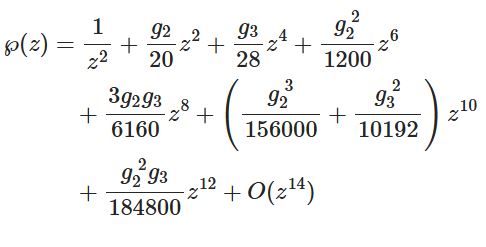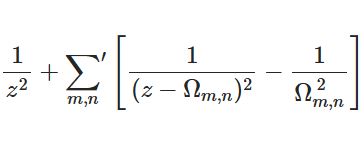複素積分演習（真性特異点）

@infseriesbot より。

見通しやすい形にする

むちゃくちゃな積分に見えますが、意外にそうでもないです。\begin{eqnarray*}I &=& \frac{1}{2}\int_0^\pi \exp(e^{\cos x}\cos\sin x)\left[\exp(ie^{\cos x}\sin\sin x)+\exp(-ie^{\cos x}\sin\sin x)\right]dx \\&=& \frac{1}{2}\int_0^\pi\left[\exp(e^{\cos x}e^{i\sin x})+\exp(e^{\cos x}e^{-i\sin x})\right]dx \\&=&\frac{1}{2}\int_0^\pi\left[\exp(e^{e^{ix}})+\exp(e^{e^{-ix}})\right]dx\\&=&\frac{1}{4}\int_0^{2\pi}\left[\exp(e^{e^{ix}})+\exp(e^{e^{-ix}})\right]dx\end{eqnarray*}$z=e^{ix}$ とおくと $z$ は半径 $1$ の円を描きますが、$z=0$ 以外で正則であることから、原点を回るのであればどんな経路でもいいです。この経路を $(0+)$ と表しますと\begin{eqnarray*}I &=& \frac{1}{4i}\int^{(0+)}\frac{\exp(e^{z})+\exp(e^{1/z})}{z}dz\\ &=& \frac{1}{4i}\left(\underbrace{\int^{(0+)}\frac{\exp(e^{z})}{z}dz}_{J}+\underbrace{\int^{(0+)}\frac{\exp(e^{1/z})}{z}dz}_{K}\right)\end{eqnarray*}

積分の実行

$J$ は $z=0$ に1位の極をもちます。留数定理により$$J=2\pi i\exp(e^{0})=2\pi i e$$$K$ は $z=0$ に真性特異点をもちます。ローラン展開したときの $a_{-1}$ すなわち留数を求めましよう。$$\exp(e^{1/z})=1+e^{1/z}+\frac{e^{2/z}}{2!}+\frac{e^{3/z}}{3!}\cdots$$および$$e^{n/z}=1+\frac{n}{z}+\frac{1}{2!}\frac{n^2}{z^2}+\cdots$$より$\dfrac{\exp(e^{1/z})}{z}$ の留数は $$a_{-1}=1+1+\frac{1}{2!}+\frac{1}{3!}\cdots=e$$$$\therefore\quad K=2\pi i e$$以上から

応援のおねがい

Please support me!

まめしば

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。

ご支援いただいた方は、こちらで確認できます。

◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。

◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。

OFUSEで応援を送る

◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。