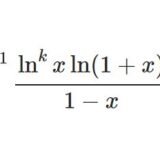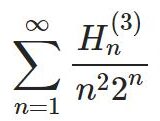前回はこちら:
weight5の積分やEuler-sumを扱います。
\begin{align}\int_0^1\frac{\ln^3(1-x)\ln(1+x)}{x}dx &=-\frac{81}{16}\zeta(5)+6\Li_5\left(\frac{1}{2}\right)+6\Li_4\left(\frac{1}{2}\right)\ln2\\&\quad-\frac{21}{8}\zeta(3)\zeta(2)+\frac{21}{8}\zeta(3)\ln^22-\zeta(2)\ln^32+\frac{1}{5}\ln^52\\ \int_0^\frac{1}{2}\frac{\Li_4(x)}{1-x}dx &=\frac{27}{32}\zeta(5)-2\Li_5\left(\frac{1}{2}\right)-\Li_4\left(\frac{1}{2}\right)\ln2\\&\quad+\frac{7}{16}\zeta(3)\zeta(2)-\frac{7}{16}\zeta(3)\ln^22+\frac{1}{6}\zeta(2)\ln^32-\frac{1}{30}\ln^52\\\int_0^\frac{1}{2}\frac{\Li_2^{~2}(x)}{x}dx&=\frac{27}{32}\zeta(5)-2\Li_5\left(\frac{1}{2}\right)-2\Li_4\left(\frac{1}{2}\right)\ln2-\frac{5}{8}\zeta(4)\ln 2\\&\quad+\frac{7}{8}\zeta(3)\zeta(2)-\frac{7}{8}\zeta(3)\ln^22+\frac{1}{2}\zeta(2)\ln^32-\frac{7}{60}\ln^52\\\sum_{n=1}^\infty\frac{H_n^{(4)}}{n2^n} &=\frac{27}{32}\zeta(5)-\Li_5\left(\frac{1}{2}\right)-\Li_4\left(\frac{1}{2}\right)\ln2\\&\quad+\frac{7}{16}\zeta(3)\zeta(2)-\frac{7}{16}\zeta(3)\ln^22+\frac{1}{6}\zeta(2)\ln^32-\frac{1}{30}\ln^52\\\sum_{n=1}^\infty\frac{H_{n-1}^{(4)}}{n2^n} &=\frac{27}{32}\zeta(5)-2\Li_5\left(\frac{1}{2}\right)-\Li_4\left(\frac{1}{2}\right)\ln2\\&\quad+\frac{7}{16}\zeta(3)\zeta(2)-\frac{7}{16}\zeta(3)\ln^22+\frac{1}{6}\zeta(2)\ln^32-\frac{1}{30}\ln^52\end{align}
はじめに$$\int_0^1\frac{\ln^3(1-x)\ln(1+x)}{x}dx$$を計算します。\begin{equation}\frac{a^4}{4}-\frac{b^4}{4}+\frac{(a+b)^4}{16}-\frac{5}{16}(a-b)^4-\frac{1}{2}b(a-b)^3=a^3b\tag{1}\end{equation}において $a=\ln(1-x)$ , $b=\ln(1+x)$ とすることで\begin{align}\int_0^1\frac{\ln^3(1-x)\ln(1+x)}{x}dx &= \frac{1}{4}\underbrace{\int_0^1\frac{\ln^4(1-x)}{x}dx}_{I_1}-\frac{1}{4}\underbrace{\int_0^1\frac{\ln^4(1+x)}{x}dx}_{I_2}+\frac{1}{16}\underbrace{\int_0^1\frac{\ln^4(1-x^2)}{x}dx}_{I_3}\\&\quad-\frac{5}{16}\underbrace{\int_0^1\frac{\ln^4(\frac{1-x}{1+x})}{x}dx}_{I_4}-\frac{1}{2}\underbrace{\int_0^1\frac{\ln^3(\frac{1-x}{1+x})\ln(1+x)}{x}dx}_{I_5}\end{align}と5つの積分に分けられます。
過去記事より\begin{align}\int_0^1\frac{\ln^k(1-x)}{x}dx&=(-1)^kk!\zeta(k+1)\tag{2}\\\int_0^1\frac{\ln^k(1-x^2)}{x}dx&=\frac{1}{2}(-1)^kk!\zeta(k+1)\tag{3}\\\int_0^1\frac{\ln^k(\frac{1-x}{1+x})}{x}dx&=2\cdot(-1)^kk!\left(1-\frac{1}{2^{k+1}}\right)\zeta(k+1)\tag{4}\\\int_0^1\frac{\ln^k(1+x)}{x}dx&=-\frac{k\ln^{k+1}2}{k+1}+k!\zeta(k+1)-\sum_{r=1}^k\binom{k}{r}r!\Li_{r+1}\left(\frac{1}{2}\right)\ln^{k-r}2\tag{5}\\\int_0^1\frac{\ln^kx}{1-x^2}dx&=(-1)^kk!\left(1-\frac{1}{2^{k+1}}\right)\zeta(k+1)\tag{6}\\\end{align}から\begin{align}\int_0^1\frac{\ln^4(1-x)}{x}dx&=24\zeta(5)\tag{7}\\\int_0^1\frac{\ln^4(1-x^2)}{x}dx&=12\zeta(5)\tag{8}\\\int_0^1\frac{\ln^4(\frac{1-x}{1+x})}{x}dx&=\frac{93}{2}\zeta(5)\tag{9}\\\int_0^1\frac{\ln^4(1+x)}{x}dx&=24\zeta(5)-24\Li_5\left(\frac{1}{2}\right)-24\Li_4\left(\frac{1}{2}\right)\ln2\\&\quad-\frac{21}{2}\zeta(3)\ln^22+4\zeta(2)\ln^32-\frac{4}{5}\ln^52\tag{10}\\\int_0^1\frac{\ln^3x}{1-x^2}dx&=-\frac{45}{8}\zeta(4)\tag{11}\\\end{align}(7)~(10)はそれぞれ $I_1,I_3,I_4,I_2$ ですので、残りは $I_5$ だけです。$I_5$ では $y=\frac{1-x}{1+x}$ と置換します。$$I_5=2\ln2\int_0^1\frac{\ln^3y}{1-y^2}dy-2\int_0^1\frac{\ln^3y\ln(1+y)}{1-y^2}dy$$第1項は(11)で求まります。第2項は部分分数分解します。$$I_5=-\frac{45}{4}\zeta(4)\ln2-\underbrace{\int_0^1\frac{\ln^3x\ln(1+x)}{1+x}dx}_{I_6}-\underbrace{\int_0^1\frac{\ln^3x\ln(1+x)}{1-x}dx}_{I_7}$$こちらの記事より\begin{equation}\int_0^1\frac{\ln^{2k-1}x\ln(1+x)}{1+x}dx=(2k-1)!\left[-\sum_{l=0}^{k-1}\eta(2l)\zeta(2k-2l+1)+\frac{2k-1}{2}\eta(2k+1)\right]\tag{12}\end{equation}と分かっていますので $k=2$ として\begin{equation}I_6=\int_0^1\frac{\ln^3x\ln(1+x)}{1+x}dx=\frac{87}{16}\zeta(5)-3\zeta(2)\zeta(3)\tag{13}\end{equation}一方、こちらの記事より\begin{align}\int_0^1\frac{\ln^kx\ln(1+x)}{1-x}dx&=\frac{(-1)^{k+1}}{2}(k+1)!\zeta(k+2)\\&\quad+2(-1)^kk!\left(1-\frac{1}{2^{k+1}}\right)\zeta(k+1)\ln2\\&\quad+\frac{(-1)^k}{2}k!\sum_{r=2}^k\left(1-\frac{1}{2^{r-1}}\right)\left(1-\frac{1}{2^{k-r+1}}\right)\zeta(r)\zeta(k-r+2)\tag{14}\end{align}でしたから、$k=3$ として\begin{align}I_7=\int_0^1\frac{\ln^3x\ln(1+x)}{1-x}dx=12\zeta(5)-\frac{45}{4}\zeta(4)\ln2-\frac{9}{4}\zeta(2)\zeta(3)\tag{15}\end{align}以上から $I_5$ が求まります。すなわち\begin{equation}\int_0^1\frac{\ln^3(\frac{1-x}{1+x})\ln(1+x)}{x}dx=-\frac{279}{16}\zeta(5)+\frac{21}{4}\zeta(2)\zeta(3)\tag{16}\end{equation}最終的に目標の積分が次のように求まります。
\begin{align}\int_0^1\frac{\ln^3(1-x)\ln(1+x)}{x}dx &=-\frac{81}{16}\zeta(5)+6\Li_5\left(\frac{1}{2}\right)+6\Li_4\left(\frac{1}{2}\right)\ln2\\&\quad-\frac{21}{8}\zeta(3)\zeta(2)+\frac{21}{8}\zeta(3)\ln^22-\zeta(2)\ln^32+\frac{1}{5}\ln^52\end{align}
自然数 $p$ に対し\begin{align}\int_0^1\frac{\ln^px\:(1-x^n)}{1-x}dx &=\int_0^1\ln^px (1+x+\cdots+x^{n-1})dx\\&=\sum_{k=1}^n\int_0^1x^{k-1}\ln^pxdx \\&=(-1)^pp!\sum_{k=1}^n\frac{1}{k^{p+1}}\end{align}最後は部分積分を繰り返しました。したがって\begin{equation}H_n^{(p)} =\frac{(-1)^{p-1}}{(p-1)!}\int_0^1\frac{1-x^n}{1-x}\ln^{p-1}xdx\tag{17}\end{equation}(17)を使うと\begin{align}(-1)^{p-1}(p-1)!\sum_{n=1}^\infty\frac{H_n^{(p)}}{n2^n} &=\int_0^1\frac{\ln^{p-1}x}{1-x}\sum_{n=1}^\infty\frac{1-x^n}{n2^n} dx \\&=\int_0^1\frac{\ln^{p-1}x}{1-x}\sum_{n=1}^\infty\left(\frac{(1/2)^n}{n}-\frac{(x/2)^n}{n}\right)dx\end{align}メルカトル級数から\begin{align}&=\int_0^1\frac{\ln^{p-1}x}{1-x}\left(\ln2+\ln\left(1-\frac{x}{2}\right)\right)dx\\&=\int_0^1\frac{\ln^{p-1}x\ln(2-x)}{1-x}dx\end{align}$x$ を $1-x$ と置換すれば
$$\int_0^1\frac{\ln^{p-1}(1-x)\ln(1+x)}{x}dx =(-1)^{p-1}(p-1)!\sum_{n=1}^\infty\frac{H_n^{(p)}}{n2^n}$$
これから分かるように、左辺の積分が計算できれば右辺のEuler-sumが計算できるようになります。$p=4$ として定理13より
\begin{align}\sum_{n=1}^\infty\frac{H_n^{(4)}}{n2^n} &=\frac{27}{32}\zeta(5)-\Li_5\left(\frac{1}{2}\right)-\Li_4\left(\frac{1}{2}\right)\ln2\\&\quad+\frac{7}{16}\zeta(3)\zeta(2)-\frac{7}{16}\zeta(3)\ln^22+\frac{1}{6}\zeta(2)\ln^32-\frac{1}{30}\ln^52\end{align}\begin{align}\sum_{n=1}^\infty\frac{H_{n-1}^{(4)}}{n2^n} &=\frac{27}{32}\zeta(5)-2\Li_5\left(\frac{1}{2}\right)-\Li_4\left(\frac{1}{2}\right)\ln2\\&\quad+\frac{7}{16}\zeta(3)\zeta(2)-\frac{7}{16}\zeta(3)\ln^22+\frac{1}{6}\zeta(2)\ln^32-\frac{1}{30}\ln^52\end{align}
定理15の2つめは、1つめにおいて $H_n^{(4)}=H_{n-1}^{(4)}+1/n^4$ を使えばすぐに導けます。
さらにこちらの2023/2/18から\begin{equation}\sum_{n=0}^\infty H_n^{(p)}x^n=\frac{\Li_p(x)}{1-x}\tag{18}\end{equation}ここで $H_0^{(p)}:=0$ です。$p=4$ として(18)を $0$ から $1/2$ まで積分すると\begin{equation}\int_0^\frac{1}{2}\frac{\Li_4(x)}{1-x}dx=\sum_{n=1}^\infty\frac{H_{n-1}^{(4)}}{n2^n}\tag{19}\end{equation}なので定理15をそのまま援用できます。
\begin{align}\int_0^\frac{1}{2}\frac{\Li_4(x)}{1-x}dx &=\frac{27}{32}\zeta(5)-2\Li_5\left(\frac{1}{2}\right)-\Li_4\left(\frac{1}{2}\right)\ln2\\&\quad+\frac{7}{16}\zeta(3)\zeta(2)-\frac{7}{16}\zeta(3)\ln^22+\frac{1}{6}\zeta(2)\ln^32-\frac{1}{30}\ln^52\end{align}
また、部分積分により\begin{align}\int_0^\frac{1}{2}\frac{\Li_2^{~2}(x)}{x}dx &=\Li_3\left(\frac{1}{2}\right)\Li_2\left(\frac{1}{2}\right)+\int_0^\frac{1}{2}\frac{\Li_3(x)\ln(1-x)}{x}dx \\&= \Li_3\left(\frac{1}{2}\right)\Li_2\left(\frac{1}{2}\right)-\Li_4\left(\frac{1}{2}\right)\ln 2+\int_0^\frac{1}{2}\frac{\Li_4(x)}{1-x}dx\end{align}$\Li_3(1/2)$ , $\Li_2(1/2)$ はこちらで求めていますので、系16とあわせて
\begin{align}\int_0^\frac{1}{2}\frac{\Li_2^{~2}(x)}{x}dx&=\frac{27}{32}\zeta(5)-2\Li_5\left(\frac{1}{2}\right)-2\Li_4\left(\frac{1}{2}\right)\ln2-\frac{5}{8}\zeta(4)\ln 2\\&\quad+\frac{7}{8}\zeta(3)\zeta(2)-\frac{7}{8}\zeta(3)\ln^22+\frac{1}{2}\zeta(2)\ln^32-\frac{7}{60}\ln^52\end{align}
今回はここまで。次は関連したweight5のEuler-sumをさらに作っていきます:
調和数を含んだ級数(Euler-sum)とゼータ関数 part17
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。