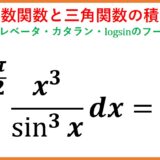Integrals and Miscellaneous 5

\begin{eqnarray*}I&&\equiv\int_0^\frac{\pi}{2}\frac{\tan xdx}{4\ln^2\tan x+\pi^2}\\&&=\int_0^\infty\frac{xdx}{(4\ln^2x+\pi^2)(1+x^2)}\\&&=\int_0^1\frac{xdx}{(4\ln^2x+\pi^2)(1+x^2)}+\int_1^\infty\frac{xdx}{(4\ln^2x+\pi^2)(1+x^2)}\\&&=\int_0^1\frac{(x+\frac{1}{x})dx}{(4\ln^2x+\pi^2)(1+x^2)}\\&&=\int_0^1\frac{dx}{x(4\ln^2x+\pi^2)}\\&&=\int_0^\infty\frac{e^{-x}dx}{(4x^2+\pi^2)e^{-x}}\\&&=\int_0^\infty\frac{dx}{4x^2+\pi^2}\\&&=\frac{1}{4}\end{eqnarray*}More generally,\begin{eqnarray*}\int_0^\frac{\pi}{2}\frac{\tan xdx}{m\ln^2\tan x+\pi^n} &=& \int_0^\infty\frac{dx}{mx^2+\pi^n} \\&=& \frac{\pi^{1-\frac{n}{2}}}{2\sqrt{m}}\end{eqnarray*}

\begin{eqnarray*}I&&\equiv\int_0^\frac{\pi}{2}\frac{x^2}{\sin^2x}dx\\&&=\left[-x^2\cot x\right]_0^\frac{\pi}{2}+\int_0^\frac{\pi}{2}2x\cot xdx\\&&=2\int_0^\frac{\pi}{2}x\cot xdx\\&&=\left[2x\ln\sin x\right]_0^\frac{\pi}{2}-2\int_0^\frac{\pi}{2}\ln\sin xdx\\&&=-2\int_0^\frac{\pi}{2}\ln\sin xdx\\&&=\pi\ln2\end{eqnarray*}

\begin{eqnarray*}I&&\equiv\int_0^\frac{\pi}{2}\frac{x^3}{\sin^3x}dx\\&&=\left[\frac{x^3}{2}\left(\ln\tan\frac{x}{2}-\frac{\cos x}{\sin^2x}\right)\right]_0^\frac{\pi}{2}-\frac{3}{2}\int_0^\frac{\pi}{2}x^2\left(\ln\tan\frac{x}{2}-\frac{\cos x}{\sin^2x}\right)dx\\&&=\frac{3}{2}\int_0^\frac{\pi}{2}x^2\left(\frac{\cos x}{\sin^2x}-\ln\tan\frac{x}{2}\right)dx\end{eqnarray*}

\begin{eqnarray*}\int_0^\frac{\pi}{2}x^2\frac{\cos x}{\sin^2x}&&=\left[-\frac{x^2}{\sin x}\right]_0^\frac{\pi}{2}+2\int_0^\frac{\pi}{2}\frac{x}{\sin x}dx\\&&=-\frac{\pi^2}{4}+4G\end{eqnarray*}

\begin{eqnarray*}\int_0^\frac{\pi}{2}x^2\ln\tan\frac{x}{2}dx&&=8\int_0^\frac{\pi}{4}x^2\ln\tan xdx\\&&=-16\int_0^\frac{\pi}{4}x^2\sum_{n=0}^\infty \frac{\cos(4n+2)x}{2n+1}dx\\&&=-16\sum_{n=0}^\infty\frac{1}{2n+1}\int_0^\frac{\pi}{4}x^2\cos(4n+2)xdx\\&&=-16\sum_{n=0}^\infty\frac{1}{2n+1}\left(\frac{(-1)^n\pi^2}{32(2n+1)}-\frac{(-1)^n}{4(2n+1)^3}\right)\\&&=-\frac{\pi^2}{2}G+4\beta(4)\end{eqnarray*}Hence,$$\int_0^\frac{\pi}{2}\frac{x^3}{\sin^3x}dx=-\frac{3}{8}\pi^2+\left(6+\frac{3}{4}\pi^2\right)G-6\beta(4)$$

\begin{eqnarray*}\sum_{n=1}^\infty\frac{1}{(n+a)(n+b)}&&=\frac{1}{b-a}\sum_{n=1}^\infty\left(\frac{1}{n+a}-\frac{1}{n+b}\right)\\&&=\frac{1}{b-a}\sum_{n=0}^\infty\left(\frac{1}{n+a+1}-\frac{1}{n+1}-\frac{1}{n+b+1}+\frac{1}{n+1}\right)\\&&=\frac{1}{b-a}\left[-\g-\sum_{n=0}^\infty\left(\frac{1}{n+b+1}-\frac{1}{n+1}\right)+\g+\sum_{n=0}^\infty\left(\frac{1}{n+a+1}-\frac{1}{n+1}\right)\right]\\&&=\frac{\psi(b+1)-\psi(a+1)}{b-a}\end{eqnarray*}

\begin{eqnarray*}\int_0^\infty\frac{1-e^{-x^2}}{x^2}dx&&=\lim_{\epsilon\to0}\int_\epsilon^\infty\frac{1-e^{-x^2}}{x^2}dx\\&=&\lim_{\epsilon\to0}\frac{1-e^{-\epsilon^2}}{\epsilon}+\int_0^\infty2e^{-x^2}dx\\&=&\lim_{\epsilon\to0}\frac{1-e^{-\epsilon^2}}{\epsilon}+\sqrt{\pi}\\&=&\lim_{\epsilon\to0}\frac{1-1+O(\epsilon^2)}{\epsilon}+\sqrt{\pi}\\&=&\sqrt{\pi}\end{eqnarray*}

$$I=\displaystyle\int_{-\infty}^\infty \frac{e^{-x^2}}{1+x^2}dx$$

Define $\displaystyle f(a)\equiv \int_{-\infty}^\infty \frac{e^{-a^2x^2}}{1+x^2}dx$ .Then $I=f(1),f(0)=\pi$.
$$f^\prime(a)=2af(a)-2\sqrt{\pi}$$
$$\therefore f(a)=\left(-2\sqrt{\pi}\int_0^a e^{-x^2}dx+f(0) \right)e^{a^2}=\pi(1-\mathrm{erf}(a))e^{a^2}$$
$$\therefore I=f(1)=\pi e(1-\rm{erf}(1))$$

$$I=\displaystyle\int_0^1 x^{-x}dx$$

$$I=\int_0^1 e^{-x\log x}dx=\int_0^1 \sum_{n=0}^\infty \frac{(-x\log x)^n}{n!}=\sum_{n=0}^\infty \frac{(-1)^n}{n!}\int_0^1(x\log x)^ndx$$$$I_n \equiv \int_0^1(x\log x)^ndx =-\frac{n}{n+1}\int_0^1 x^n(\log x)^{n-1}dx$$繰り返して，$$I_n=(-1)^n\frac{n!}{(n+1)^{n+1}}$$$$\therefore I=\sum_{n=0}^\infty \frac{(-1)^n}{n!}(-1)^n\frac{n!}{(n+1)^{n+1}}$$$$\therefore \int_0^1 x^{-x}dx = \sum_{n=1}^\infty \frac{1}{n^n}$$

$$I=\int_{-\infty}^\infty\frac{\sin x}{x}dx$$Consider $\displaystyle\oint_C\frac{e^{iz}}{z}dz$ ,where $C$ is the big semi-circle on the upper half-plane.

The value of the big arc tends to zero because:$$\left|\int_{\mathrm{arc}}\right|\le\int_0^\pi e^{-R\sin\t}d\t\le\frac{\pi}{R}(1-e^{-R})\longrightarrow 0$$The residue of the origin is:$$\displaystyle\lim_{z\to 0}e^{iz}=1$$Hence,$$0=\int_{-\infty}^\infty\frac{e^{ix}}{x}dx+(-\pi i)+0$$Hence,$$I=\pi$$

\begin{eqnarray*}I&&\equiv\int_{-\infty}^\infty\frac{\sin^2 x}{x^2}dx\\&&=\left[-\frac{\sin^2x}{x}\right]_{-\infty}^{\infty}+2\int_{-\infty}^\infty\frac{\sin x\cos x}{x}dx\\&&=\int_{-\infty}^\infty\frac{\sin 2x}{x}dx\\&&=\int_{-\infty}^\infty\frac{\sin x}{x}dx\\&&=\pi\end{eqnarray*}

\begin{eqnarray*}I&&\equiv\int_{-\infty}^\infty\frac{\sin^3 x}{x^3}dx\\&&=\left[-\frac{\sin^3x}{2x^2}\right]_{-\infty}^\infty+\frac{3}{2}\int_{-\infty}^\infty\frac{\sin^2x\cos x}{x^2}dx\\&&=\frac{3}{2}\left[-\frac{\sin^2x\cos x}{x}\right]_{-\infty}^\infty+\frac{3}{2}\int_{-\infty}^\infty\frac{2\sin x\cos^2 x-\sin^3x}{x}dx\\&&=\frac{3}{8}\int_{-\infty}^\infty\frac{-\sin x+3\sin 3x}{x}dx\\&&=\frac{3}{8}(-\pi+3\pi)\\&&=\frac{3}{4}\pi\end{eqnarray*}

\begin{eqnarray*}I&&\equiv\int_{-\infty}^\infty\frac{\sin^4 x}{x^4}dx\\&&=\frac{4}{3}\int_{-\infty}^\infty\frac{\sin^3x\cos x}{x^3}dx\\&&=\frac{2}{3}\int_{-\infty}^\infty\frac{3\sin^2 x-4\sin^4x}{x^2}dx\\&&=\frac{4}{3}\int_0^\infty(3-4\sin^2x)\frac{\sin^2x}{x^2}dx\end{eqnarray*}Using Lobachevsky integral formula we find\begin{eqnarray*}&&=\frac{4}{3}\int_0^\frac{\pi}{2}(3-4\sin^2x)dx\\&&=\frac{2}{3}\pi\end{eqnarray*}

\begin{eqnarray*}I&&\equiv\int_0^\frac{\pi}{4}(-\ln\tan x)^{s-1}dx\\&&=\int_0^1\frac{(-\ln y)^{s-1}}{1+y^2}dy\quad(y=\tan x)\\&&=\int_0^\infty\frac{u^{s-1}e^{-u}}{1+e^{-2u}}du\quad(-\ln y=u)\\&&=\G(s)\beta(s)\end{eqnarray*}

$$I=\int_0^\infty\frac{xdx}{(1+x^2)(e^{2\pi x}-1)}\;,\;J=\int_0^\infty\frac{xdx}{(1+x^2)^2(e^{2\pi x}-1)}$$Binet's second formula:$$\log\G(z)=\left(z-\frac{1}{2}\right)\log z-z+\frac{1}{2}\log2\pi+2\int_0^\infty\frac{\arctan\frac{t}{z}}{e^{2\pi t}-1}dt$$The first and second derivative of this are:$$\psi(z)=-\frac{1}{2z}+\ln z-2\int_0^\infty\frac{tdt}{(z^2+t^2)(e^{2\pi t}-1)}$$$$\psi'(z)=\frac{1}{2z^2}+\frac{1}{z}+\int_0^\infty\frac{4tzdt}{(z^2+t^2)^2(e^{2\pi t}-1)}$$Substituting $z=1$ to them, we obtain$$I=\frac{\g}{2}-\frac{1}{4}\;,\;J=\frac{\pi^2}{24}-\frac{3}{8}$$since $\psi(1)=-\g$ , $\psi'(1)=\zeta(2)$.

$$I=\int_0^1\frac{2x\arctan x+\ln(1+x^2)}{1+x^2}dx$$The first term:\begin{eqnarray*}\int_0^1\frac{2x\arctan x}{1+x^2}dx&&=\left[\ln(1+x^2)\cdot \arctan x\right]_0^1-\int_0^1\frac{\ln(1+x^2)}{1+x^2}dx\\&&=\frac{\pi\ln2}{4}-\int_0^1\frac{\ln(1+x^2)}{1+x^2}dx\end{eqnarray*}Hence,$$I=\frac{\pi\ln2}{4}$$

\begin{eqnarray*}I&&\equiv \int_0^\frac{\pi}{2}\frac{dx}{(1+\tan x)^6}\\&&=\int_0^\infty\frac{dx}{(1+x)^6(1+x^2)}\\&&=\int_0^\infty\Bigl(\frac{x}{8(x^2+1)}-\frac{1}{8(x+1)}-\frac{1}{8(x+1)^2}\\&&\quad+\frac{1}{4(x+1)^4}+\frac{1}{2(x+1)^5}+\frac{1}{2(x+1)^6}\Bigr)dx\\&&=\Bigl[\frac{1}{16}\ln\frac{1+x^2}{(1+x)^2}+\frac{1}{8(x+1)}-\frac{1}{12(x+1)^3}\\&&\quad-\frac{1}{8(x+1)^4}-\frac{1}{10(x+1)^5}\Bigr]_0^\infty\\&&=\frac{11}{60}\end{eqnarray*}

\begin{eqnarray*}I&&\equiv\int_0^\pi\frac{\ln(1+\frac{\cos x}{2})}{\cos x}dx\\&&=\int_0^\pi\frac{1}{\cos x}\sum_{n=1}^\infty\frac{(-1)^{n-1}\cos^nx}{n2^n}dx\end{eqnarray*}Since $\int_0^\pi \cos^{2n+1}xdx=0$, odd terms vanish. Calculating the integral, we get\begin{eqnarray*}I&&=\sum_{n=0}^\infty\frac{1}{2n+1}\frac{\pi}{2^{2n+1}}\frac{(2n-1)!!}{(2n)!!}\\&&=\frac{\pi}{4}\sum_{n=0}^\infty\frac{2(\frac{1}{2})_n(\frac{1}{2})_n}{4^n(\frac{3}{2})_n n!}\\&&=\frac{\pi}{2}{}_2F_1\left[\begin{matrix}\frac{1}{2},\frac{1}{2}\\\frac{3}{2}\end{matrix};\frac{1}{4}\right]\\&&=\frac{\pi}{2}\frac{\arcsin\frac{1}{2}}{\frac{1}{2}}\\&&=\frac{\pi^2}{6}\\&&=\zeta(2)\end{eqnarray*}

Using the series representation of digamma function,$$\sum_{n=1}^\infty\frac{1}{n(kn+1)}=\g+k+\psi\left(\frac{1}{k}\right)$$And the special values of digamma function:\begin{eqnarray*}\psi\left(\frac{1}{2}\right)&&=-\g-2\log2\\\psi\left(\dfrac{1}{3}\right)&&=-\g-\frac{3}{2}\log3-\frac{\pi}{2\sqrt{3}}\\\psi\left(\dfrac{1}{4}\right)&&=-\g-3\log2-\frac{\pi}{2}\\\psi\left(\frac{1}{6}\right)&&=-\g-\frac{3}{2}\ln3-2\ln2-\frac{\sqrt{3}}{2}\pi\end{eqnarray*}Hence,\begin{eqnarray*}\sum_{n=1}^\infty\frac{1}{n(2n+1)}&&=2-2\ln2\\\sum_{n=1}^\infty\frac{1}{n(3n+1)}&&=3-\frac{3}{2}\ln3-\frac{\pi}{2\sqrt{3}}\\\sum_{n=1}^\infty\frac{1}{n(4n+1)}&&=4-3\ln2-\frac{\pi}{2}\\\sum_{n=1}^\infty\frac{1}{n(6n+1)}&&=6-\frac{3}{2}\ln3-2\ln2-\frac{\sqrt{3}}{2}\pi\end{eqnarray*}

$$\sum_{n=1}^\infty H_nx^n=-\frac{\log(1-x)}{1-x}$$

Series expansions of $-\log(1-x)$ and $\frac{1}{1-x}$:\begin{eqnarray*}-\log(1-x)&&=\sum_{n=1}^\infty\frac{x^n}{n}\\\frac{1}{1-x}&&=\sum_{n=0}^\infty x^n\end{eqnarray*}The Cauchy product of these two series is$$-\frac{\log(1-x)}{1-x}=\sum_{n=1}^\infty\left(\sum_{k=1}^n\frac{1}{k}\right)x^n$$Then we obtain the red equation above.

$$H_n=-4n\int_0^\frac{\pi}{2}\sin x\cos^{2n-1}x(\ln\sin x)dx$$

Using the partial derivative of the beta function:$$\dd{B(p,q)}{p}=4\int_0^\frac{\pi}{2}\sin^{2p-1}x\cos^{2q-1}x(\ln\sin x)dx$$Substituting $p=1$ , $q=n$ ,\begin{eqnarray*}-4n\int_0^\frac{\pi}{2}\sin x\cos^{2n-1}x(\ln\sin x)dx&&=-n\left.\dd{B(p,q)}{p}\right|_{p=1,q=n}\\&&=-n\left.B(p,q)\Bigl(\psi(p)-\psi(p+q)\Bigr)\right|_{p=1,q=n}\\&&=-n\frac{(n-1)!}{n!}(-H_n)\\&&=H_n\end{eqnarray*}

\begin{eqnarray*}\sum_{n=1}^\infty\frac{H_n}{n^2}&&=\sum_{n=1}^\infty\sum_{k=1}^n\frac{1}{n^2k}\\&&=\sum_{k=1}^\infty\sum_{n=k}^\infty\frac{1}{n^2k}\\&&=\sum_{k=1}^\infty\left(\frac{1}{k^3}+\sum_{n=k+1}^\infty\frac{1}{n^2k}\right)\\&&=\zeta(3)+\sum_{k=1}^\infty\sum_{n=1}^\infty\frac{1}{(n+k)^2k}\\&&=\zeta(3)+\frac{1}{2}\sum_{k=1}^\infty\sum_{n=1}^\infty\left(\frac{1}{(n+k)^2k}+\frac{1}{(k+n)^2n}\right)\\&&=\zeta(3)+\frac{1}{2}\sum_{k=1}^\infty\sum_{n=1}^\infty\frac{1}{nk(n+k)}\\&&=\zeta(3)+\frac{1}{2}\sum_{k=1}^\infty\frac{1}{k^2}\sum_{n=1}^\infty\left(\frac{1}{n}-\frac{1}{n+k}\right)\\&&=\zeta(3)+\frac{1}{2}\sum_{k=1}^\infty\frac{1}{k^2}H_k\end{eqnarray*}Hence,$$\sum_{n=1}^\infty\frac{H_n}{n^2}=2\zeta(3)$$