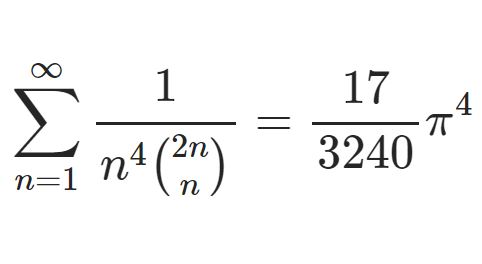前回は $\sin x$ を含んだ対数正弦積分(log-sine integral)に取り組みました。
log(sin x)の2乗の対数正弦積分(調和数・ポリログ)
今回は被積分関数に $\ln(2\sinh x)$ が含まれるものを考えます。$\sinh$ なので「正弦」ではありませんが、話の筋は結構似ていますので、その類似性からこのようなタイトルにしました。
調和数 $H_n=1+\frac{1}{2}+\cdots+\frac{1}{n}\;,\;H_0=0$ とする。また黄金比を $\phi=\frac{\sqrt{5}+1}{2}$ と書く。
Part 1\begin{equation}\int_0^x\ln(2\sinh x)dx=\frac{x^2}{2}-\frac{\pi^2}{12}+\frac{1}{2}\Li_2\left(e^{-2x}\right)\end{equation}これを用いれば次を得ることができる。\begin{eqnarray}\int_0^{\frac{\ln2}{2}}\ln(2\sinh x)dx &=& -\frac{\pi^2}{24}-\frac{\ln^22}{8} \\ \int_0^{\ln\phi}\ln(2\sinh x)dx &=& -\frac{\pi^2}{20} \\ \int_0^{\frac{\ln\phi}{2}}\ln(2\sinh x)dx &=& -\frac{\pi^2}{30}-\frac{3}{8}\ln^2\phi\end{eqnarray}
Part 2\begin{equation}\int_0^x x\ln(2\sinh x)dx=\frac{x^3}{3}+\frac{x}{2}\Li_2\left(e^{-2x}\right)+\frac{1}{4}\Li_3\left(e^{-2x}\right)-\frac{\zeta(3)}{4}\end{equation}これを用いれば次を得ることができる。\begin{eqnarray}\int_0^{\frac{\ln2}{2}}x\ln(2\sinh x)dx &=& -\frac{\zeta(3)}{32}-\frac{\ln^3 2}{24} \\ \int_0^{\ln\phi}x\ln(2\sinh x)dx &=& -\frac{\zeta(3)}{20} \\ \int_0^{\frac{\ln\phi}{2}}x\ln(2\sinh x)dx &=& \frac{1}{4}\Li_3(\phi^{-1})+\frac{\pi^2}{40}\ln\phi-\frac{5}{24}\ln^3\phi-\frac{\zeta(3)}{4}\end{eqnarray}
Part 3\begin{eqnarray}\int_0^x \ln^2(2\sinh x)dx &=& \frac{x^3}{3}-\frac{\zeta(3)}{2}+\frac{1}{2}\Li_3(e^{-2x})+\Li_3(1-e^{-2x})\\&&+x\Li_2(e^{-2x})-\ln(1-e^{-2x})\Li_2(1-e^{-2x})+x\ln^2(1-e^{-2x})\end{eqnarray}これを用いれば次を得ることができる。\begin{eqnarray}\int_0^{\frac{\ln2}{2}} \ln^2(2\sinh x)dx &=& \frac{13}{16}\zeta(3)+\frac{\ln^3 2}{24} \\ \int_0^{\ln\phi} \ln^2(2\sinh x)dx &=& \Li_3(\phi^{-1})-\frac{\zeta(3)}{10}+\frac{\pi^2}{10}\ln\phi-\frac{\ln^3\phi}{3} \\ \int_0^{\frac{\ln\phi}{2}} \ln^2(2\sinh x)dx &=& \frac{1}{2} \Li_3(\phi^{-1})+\frac{3}{10}\zeta(3)+\frac{\pi^2}{20}\ln\phi+\frac{5}{24}\ln^3\phi\end{eqnarray}
Part 4\begin{eqnarray}\int_0^x x^2\ln(2\sinh x)dx &=& \frac{x^4}{4}-\frac{\pi^4}{360}+\frac{x^2}{2}\Li_2(e^{-2x})\\&&+\frac{x}{2}\Li_3(e^{-2x})+\frac{1}{4}\Li_4(e^{-2x})\end{eqnarray}これを用いれば次を得ることができる。\begin{eqnarray}\int_0^{\frac{\ln2}{2}}x^2\ln(2\sinh x)dx &=& \frac{1}{4}\Li_4\left(\frac{1}{2}\right)-\frac{\pi^4}{360}+\frac{7}{32}\zeta(3)\ln2-\frac{\pi^2}{96}\ln^22-\frac{\ln^42}{192} \\ \int_0^{\ln\phi}x^2\ln(2\sinh x)dx &=& \frac{1}{4}\Li_4(\phi^{-2})+\frac{2\ln\phi}{5}\zeta(3)-\frac{\pi^4}{360}-\frac{\pi^2}{30}\ln^2\phi+\frac{\ln^4\phi}{12} \end{eqnarray}
Part 5 \begin{eqnarray}\int_0^x &&x\ln^2(2\sinh x)dx\\ =&& \frac{x^4}{4}-\frac{7\pi^4}{720}+\frac{1}{2}\left[\Li_4(1-e^{-2x})-\Li_4\left(\frac{1}{1-e^{2x}}\right)\right] \\ && +x\left[\Li_3(e^{-2x})+\Li_3(1-e^{-2x})-\zeta(3)\right]+\frac{\ln(1-e^{-2x})}{2}\Li_3(e^{-2x}) \\&& +x^2\Li_2(e^{-2x})-x\ln(1-e^{-2x})\Li_2(1-e^{-2x}) -\frac{\ln^4(1-e^{-2x})}{48}\\ && -\frac{x}{6}\ln^3(1-e^{-2x})+\left(x^2-\frac{\pi^2}{24}\right)\ln^2(1-e^{-2x})-\frac{\zeta(3)}{2}\ln(1-e^{-2x})\end{eqnarray}これを用いれば次を得ることができる。\begin{eqnarray}\int_0^{\frac{\ln2}{2}}x\ln^2(2\sinh x)dx &=& \frac{1}{2}\Li_4\left(\frac{1}{2}\right)-\frac{7\pi^4}{1440}+\frac{7}{16}\zeta(3)\ln2-\frac{\pi^2}{48}\ln^22+\frac{7}{192}\ln^42\end{eqnarray}
もくじ
多重対数関数(ポリログ)の知識を多用しますので、基本事項が前提知識となります。例えば
を参考にしてください[過去記事A]。
多重対数関数の特殊値
\begin{eqnarray}\Li_2(1) &=& \zeta(2) \; ,\; \Li_2(1/2)=\frac{\pi^2}{12}-\frac{\ln^2 2}{2}\tag{0.1} \\ \Li_2(\phi^{-1})&=&\frac{\pi^2}{10}-\ln^2\phi\; ,\; \Li_2(\phi^{-2})=\frac{\pi^2}{15}-\ln^2\phi\tag{0.2} \\ \Li_3(1) &=& \zeta(3) \tag{0.3} \\ \Li_3(1/2) &=& \frac{7}{8}\zeta(3)-\frac{\pi^2}{12}\ln2+\frac{\ln^32}{6}\tag{0.4}\\ \Li_3(\phi^{-2})&=&\frac{4}{5}\zeta(3)+\frac{2}{3}\ln^3\phi-\frac{2}{15}\pi^2\ln\phi\tag{0.5}\\ \Li_4(-1)&=&-\frac{7}{8}\zeta(4)\tag{0.6}\end{eqnarray}
【証明】は過去記事A参照。この補題は以下、適宜ことわりなく用います。
調和数を含むEuler-sumの公式
\begin{equation}\sum_{n=1}^\infty\frac{H_{n-1}}{n^2} = \zeta(3) \tag{0.7}\end{equation}\begin{eqnarray}\sum_{n=1}^\infty\frac{H_n}{n^2}x^n &=& \Li_3(x)-\Li_3(1-x)+\ln(1-x)\Li_2(1-x)\\&&\quad+\frac{1}{2}\ln x\ln^2(1-x)+\zeta(3)\tag{0.8}\end{eqnarray}\begin{equation}\sum_{n=1}^\infty\frac{H_{n-1}}{n^3}=\frac{\pi^4}{360}\tag{0.9}\end{equation}\begin{eqnarray}\sum_{n=1}^\infty\frac{H_n}{n^3}x^n&=&2\Li_4(x)+\Li_4\left(\frac{x}{x-1}\right)-\Li_4(1-x)-\ln(1-x)\Li_3(x)\\&&+\frac{1}{24}\ln^4(1-x)-\frac{1}{6}\ln x\ln^3(1-x)+\frac{\pi^2}{12}\ln^2(1-x)\\&&+\zeta(3)\ln(1-x)+\frac{\pi^4}{90}\tag{0.10}\end{eqnarray}
【証明】(0.7)は過去記事C
で証明済。(0.8)は過去記事D
調和数を含んだ級数(Euler-sum)とゼータ関数 part8
で証明済。(0.9)は過去記事E
で証明済。(0.10)は導出記事未完成だが例えば S.M.Stewart, Explicit evaluation of some quadratic Euler-type sums containing double-index harmonic series,2020
不定積分の導出
$\sinh x$ の定義から\begin{equation}\ln(2\sinh x)=x+\ln(1-e^{-2x})\tag{1.1}\end{equation}$\ln (1-z)$ のマクローリン展開により\begin{equation}\ln(2\sinh x)=x-\sum_{n=1}^\infty\frac{e^{-2nx}}{n} \tag{1.2}\end{equation}と分かります。これを $0$ から $x$ まで積分すると\begin{eqnarray*}\int_0^x\ln(2\sinh x)dx &=& \frac{x^2}{2}+\frac{1}{2}\sum_{n=1}^\infty\frac{e^{-2nx}}{n^2}-\frac{\zeta(2)}{2}\end{eqnarray*}右辺第2項は二重対数関数によって書くことができます。したがって
\begin{equation}\int_0^x\ln(2\sinh x)dx=\frac{x^2}{2}-\frac{\pi^2}{12}+\frac{1}{2}\Li_2\left(e^{-2x}\right)\tag{1.3}\end{equation}
いくつかの定積分
不定積分として(1.3)を得ました。積分区間の端 $x$ に値を代入すればいろいろ定積分の式ができるのですが、問題は $\Li_2\left(e^{-2x}\right)$ です。これを「いい形」で計算できる $x$ の値はかなり制限されます([過去記事A]参照)。ここでは $x=\frac{\ln2}{2}$ , $\ln\phi$ , $\frac{\ln\phi}{2}$ としましょう。$\phi=\frac{\sqrt{5}+1}{2}$ は黄金比です。補題1を用いれば
\begin{eqnarray}\int_0^{\frac{\ln2}{2}}\ln(2\sinh x)dx &=& -\frac{\pi^2}{24}-\frac{\ln^22}{8} \tag{1.4} \\ \int_0^{\ln\phi}\ln(2\sinh x)dx &=& -\frac{\pi^2}{20}\tag{1.5} \\ \int_0^{\frac{\ln\phi}{2}}\ln(2\sinh x)dx &=& -\frac{\pi^2}{30}-\frac{3}{8}\ln^2\phi \tag{1.6}\end{eqnarray}
不定積分の導出
(1.2)に $x$ をかけて $0$ から $x$ まで積分すると\begin{eqnarray*}\int_0^x x\ln(2\sinh x)dx &=& \frac{x^3}{3}-\sum_{n=1}^\infty\frac{1}{n}\int_0^x xe^{-2nx}dx \\ &=& \frac{x^3}{3}+\frac{x}{2}\sum_{n=1}^\infty\frac{(e^{-2x})^n}{n^2}+\frac{1}{4}\sum_{n=1}^\infty\frac{(e^{-2x})^n}{n^3}-\frac{\zeta(3)}{4}\end{eqnarray*}多重対数関数の級数による定義式より
\begin{equation}\int_0^x x\ln(2\sinh x)dx=\frac{x^3}{3}+\frac{x}{2}\Li_2\left(e^{-2x}\right)+\frac{1}{4}\Li_3\left(e^{-2x}\right)-\frac{\zeta(3)}{4}\tag{2.1}\end{equation}
いくつかの定積分
(2.1)で $x=\frac{\ln2}{2}$ , $\ln\phi$ , $\frac{\ln\phi}{2}$ とすれば、補題1も用いて
\begin{eqnarray}\int_0^{\frac{\ln2}{2}}x\ln(2\sinh x)dx &=& -\frac{\zeta(3)}{32}-\frac{\ln^3 2}{24} \tag{2.2} \\ \int_0^{\ln\phi}x\ln(2\sinh x)dx &=& -\frac{\zeta(3)}{20} \tag{2.3}\\ \int_0^{\frac{\ln\phi}{2}}x\ln(2\sinh x)dx &=& \frac{1}{4}\Li_3(\phi^{-1})+\frac{\pi^2}{40}\ln\phi-\frac{5}{24}\ln^3\phi-\frac{\zeta(3)}{4}\tag{2.4}\end{eqnarray}
不定積分の導出
過去記事B
の前半から\begin{equation}\frac{1}{2}\ln^2(1-z)=\sum_{n=1}^\infty\frac{H_{n-1}}{n}z^n\tag{3.1}\end{equation}ここで $z=e^{-2x}$ とすると$$\ln^2(1-e^{-2x})=2\sum_{n=1}^\infty\frac{H_{n-1}}{n}e^{-2nx}$$(1.1)を2乗する際にこれを用いることで\begin{equation}\ln^2(2\sinh x) = -x^2+2x\ln(2\sinh x)+2 \sum_{n=1}^\infty\frac{H_{n-1}}{n}e^{-2nx}\tag{3.2}\end{equation}積分します。$$\int_0^x \ln^2(2\sinh x)dx=-\frac{x^3}{3}+2\int_0^x x\ln(2\sinh x)dx+\sum_{n=1}^\infty\frac{H_{n-1}}{n^2}-\sum_{n=1}^\infty\frac{H_{n-1}}{n^2}(e^{-2x})^n$$右辺第2項は定理2.1を、第3項には(0.7)を使います。さらに第4項では $H_{n-1}=H_n-\frac{1}{n}$ と分けることによって\begin{equation}\int_0^x \ln^2(2\sinh x)dx=\frac{x^3}{3}+\frac{\zeta(3)}{2}+x\Li_2(e^{-2x})+\frac{3}{2}\Li_3(e^{-2x})-\sum_{n=1}^\infty\frac{H_{n}}{n^2}(e^{-2x})^n\tag{3.3}\end{equation}(3.3)右辺の最終項は(0.8)の $x$ に $e^{-2x}$ を代入すると、次の公式を得ます。
\begin{eqnarray}\int_0^x \ln^2(2\sinh x)dx &=& \frac{x^3}{3}-\frac{\zeta(3)}{2}+\frac{1}{2}\Li_3(e^{-2x})+\Li_3(1-e^{-2x})\\&&+x\Li_2(e^{-2x})-\ln(1-e^{-2x})\Li_2(1-e^{-2x})\\&&+x\ln^2(1-e^{-2x})\tag{3.4}\end{eqnarray}
いくつかの定積分
(3.4)に $x=\frac{\ln2}{2}$ , $\ln\phi$ , $\frac{\ln\phi}{2}$ を代入します。
\begin{eqnarray}\int_0^{\frac{\ln2}{2}} \ln^2(2\sinh x)dx &=& \frac{13}{16}\zeta(3)+\frac{\ln^3 2}{24}\tag{3.5} \\ \int_0^{\ln\phi} \ln^2(2\sinh x)dx &=& \Li_3(\phi^{-1})-\frac{\zeta(3)}{10}+\frac{\pi^2}{10}\ln\phi-\frac{\ln^3\phi}{3}\tag{3.6} \\ \int_0^{\frac{\ln\phi}{2}} \ln^2(2\sinh x)dx &=& \frac{1}{2} \Li_3(\phi^{-1})+\frac{3}{10}\zeta(3)+\frac{\pi^2}{20}\ln\phi+\frac{5}{24}\ln^3\phi\tag{3.7}\end{eqnarray}
(1.2)に $x^2$ をかけて積分することにより、次の定理を得ます。やることは(2.1)を導出するときと同様なので途中式は端折ります。
\begin{eqnarray}\int_0^x x^2\ln(2\sinh x)dx &=& \frac{x^4}{4}-\frac{\pi^4}{360}+\frac{x^2}{2}\Li_2(e^{-2x})\\&&+\frac{x}{2}\Li_3(e^{-2x})+\frac{1}{4}\Li_4(e^{-2x})\tag{4.1}\end{eqnarray}
$\Li_4$ の特殊値はほとんど知られておらず、(4.1)に代入する「価値のある」値というものがないような感じです。せめて$\Li_3$ と $\Li_2$ は計算できる $x=\frac{\ln2}{2}$ , $\ln\phi$ を代入します。
\begin{eqnarray}\int_0^{\frac{\ln2}{2}}x^2\ln(2\sinh x)dx &=& \frac{1}{4}\Li_4\left(\frac{1}{2}\right)-\frac{\pi^4}{360}+\frac{7}{32}\zeta(3)\ln2\\&&-\frac{\pi^2}{96}\ln^22-\frac{\ln^42}{192}\tag{4.2} \\ \int_0^{\ln\phi}x^2\ln(2\sinh x)dx &=& \frac{1}{4}\Li_4(\phi^{-2})+\frac{2\ln\phi}{5}\zeta(3)-\frac{\pi^4}{360}\\&&-\frac{\pi^2}{30}\ln^2\phi+\frac{\ln^4\phi}{12}\tag{4.3} \end{eqnarray}
(3.2)に $x$ をかけて積分します。\begin{equation}\int_0^x x\ln^2(2\sinh x)dx = 2\sum_{n=1}^\infty\frac{H_{n-1}}{n}\int_0^x xe^{-2nx}dx+2\int_0^x x^2\ln(2\sinh x)dx-\frac{x^4}{4}\tag{5.1}\end{equation}この右辺第2項は定理4.1そのままです。第1項はこれまでと同様に積分しますが、その計算の途上で補題2の(0.8)(0.10)で $x$ を $e^{-2x}$ とした式、および(0.9)を用います。なかなか大変ですが、計算すると
\begin{eqnarray}\int_0^x &&x\ln^2(2\sinh x)dx\\ =&& \frac{x^4}{4}-\frac{7\pi^4}{720}+\frac{1}{2}\left[\Li_4(1-e^{-2x})-\Li_4\left(\frac{1}{1-e^{2x}}\right)\right] \\ && +x\left[\Li_3(e^{-2x})+\Li_3(1-e^{-2x})-\zeta(3)\right]+\frac{\ln(1-e^{-2x})}{2}\Li_3(e^{-2x}) \\&& +x^2\Li_2(e^{-2x})-x\ln(1-e^{-2x})\Li_2(1-e^{-2x}) -\frac{\ln^4(1-e^{-2x})}{48}\\ && -\frac{x}{6}\ln^3(1-e^{-2x})+\left(x^2-\frac{\pi^2}{24}\right)\ln^2(1-e^{-2x})-\frac{\zeta(3)}{2}\ln(1-e^{-2x})\tag{5.2}\end{eqnarray}
$\Li_3$ と $\Li_2$ は計算できる $x=\frac{\ln2}{2}$ を代入します。(0.6)を途中で用います。
\begin{eqnarray}\int_0^{\frac{\ln2}{2}}x\ln^2(2\sinh x)dx &=& \frac{1}{2}\Li_4\left(\frac{1}{2}\right)-\frac{7\pi^4}{1440}+\frac{7}{16}\zeta(3)\ln2\\&&-\frac{\pi^2}{48}\ln^22+\frac{7}{192}\ln^42\tag{5.3}\end{eqnarray}
同様の流れで $\cosh$ を使ったものも導出可能です。一部だけ:$$\ln2\cosh x=x-\sum_{n=1}^\infty\frac{(-1)^n}{n}e^{-2nx}$$$$\int_0^x\ln(2\cosh x)dx=\frac{x^2}{2}+\frac{1}{4}\zeta(2)+\frac{1}{2}\Li_2\left(-e^{-2x}\right)$$$$\int_0^x x\ln(2\cosh x)dx=\frac{x^3}{3}+\frac{x}{2}\Li_2\left(-e^{-2x}\right)+\frac{1}{4}\Li_3\left(-e^{-2x}\right)+\frac{3\zeta(3)}{16}$$これらから直ちに $\tanh$ への応用が可能です。$$\int_0^x\ln\tanh xdx=-\frac{\pi^2}{8}+\frac{1}{2}\left(\Li_2\left(e^{-2x}\right)-\Li_2\left(-e^{-2x}\right)\right)$$$$\int_0^x x\ln\tanh xdx=-\frac{7}{16}\zeta(3)+\frac{x}{2}\left(\Li_2\left(e^{-2x}\right)-\Li_2\left(-e^{-2x}\right)\right)+\frac{1}{4}\left(\Li_3\left(e^{-2x}\right)-\Li_3\left(-e^{-2x}\right)\right)$$
$\log(\tanh x)$ を扱った記事:
対数正弦積分の記事:
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。